基于STEM教育理念的数学教学设计

谭奇 袁智强

摘要：基于STEM教育理念，整合简谐运动的知识、动态数学软件GeoGebra的应用、三角函数章节的其他教学内容以及数学实验与数据拟合活动，融入问题驱动教学法与波利亚的解题四步骤，设计和实施了《正弦函数的图像》一课教学，引导学生探究正弦函数图像的形成，归纳正弦函数简图的画法，掌握图像画法的迁移应用，了解正弦曲线的物理意义。得到教学启示：改进教学方法，探索STEM教育理念应用技能;反馈教学情况，凸显STEM教育理念应用效果;反思教学过程，探究STEM教育理念应用模式。

关键词：STEM教育正弦函数的图像简谐运动GeoGebra

21世纪以来，中国的综合国力日益强盛，但某些领域的核心技术仍然落后于美国等发达国家。许多领域核心技术的解决需要运用科学（Science）、技术（Technology）、工程（Engineering）和数学（Mathematics）有关的知识和技能。因而，在中小学教学中渗透STEM教育理念、培养掌握STEM知识和技能人才的需求变得愈发强烈。

目前，我国的STEM课程归入了部分学校的课程体系，但是还没有和必修课程密切地结合起来，主要是在校本课程、社团课程或劳技课程中，所处地位相对边缘化，且应用实践比较模式化。此外，我国的学校教学以分科式为主，设计和实施整合性的STEM教育在课程安排、教材编写、学校管理、教师培训等方面均存在一定的困难。

不过，在分科教学中借鉴STEM教育理念进行设计和实施，不失为落实STEM教育的一种有效途径。我们认为，可以基于STEM教育理念开展数学学科教学，探索在实际的STEM教育中所需要的教学技能，探究应用STEM教育理念进行数学教学的一般模式。这既在课堂中融入了跨学科学习的教育思想，又灵活运用并推广了STEM教育理念，有助于整合性STEM教育的进一步发展。

因此，我们基于STEM教育理念，整合简谐运动的知识、动态数学软件GeoGebra的应用、三角函数章节的其他教学内容以及数学实验与数据拟合活动，融入问题驱动教学法与波利亚的解题四步骤，设计和实施了《正弦函数的图像》一课教学，引导学生探究正弦函数图像的形成，归纳正弦函数简图的画法，掌握图像画法的迁移应用，了解正弦曲线的物理意义。

一、设计思路

本节课的教学主要包括五个环节：科学情境、技术融合、化繁为简、变式迁移、拓展应用。

第一步，从物理情境“简谐运动”实验中抽象出数学问题，使学生对正弦曲线有一个直观的印象。

第二步，联系正弦函数的定义方式，利用单位圆上的点探究精确的正弦函数图像，在探究活动中运用GeoGebra软件突出重点、突破难点，帮助学生认识到数学问题的本质。

第三步，归纳概括画正弦函数图像常用的步骤与方法，培养学生的抽象概括能力，提升学生的数学核心素养。运用问题驱动教学法，提出相关问题引导学生思考，然后以小组合作的形式共同拟定并实施解决问题的方案。同时，结合波利亚的解题四步骤，把教学过程分为“弄清问题—拟定计划—实现计划—回顾讨论”四个步骤，启发学生的解题思路。

第四步，根据诱导公式与适当的图形变换将所学的画图方法迁移运用到余弦函数或其他可由正弦函数变换得到的函数上。

第五步，指导学生进行简单的建模，体会曲线拟合的过程，了解正弦曲线的物理意义，为以后的学习做铺垫。

二、实施过程

（一）科学情境，切入主题

教师课前把学生分成三人一组，让每一组都准备好简易支架、硬纸板、矿泉水瓶、细沙、细绳与剪刀。课上指导学生将矿泉水瓶底扎一个小孔，做成一个漏斗;再用细绳拴住瓶口挂在简易支架上，做成一个简易单摆;在漏斗下放一块硬纸板，硬纸板中间画一条直线作为坐标系的横轴;小组合作，一名学生把漏斗灌上细沙，另一名学生将漏斗拉离平衡位置并放手使其摆动，同时第三名学生匀速拉动硬纸板。在硬纸板上得到一条曲线（如图1）。

教师指出：这（近似）是简谐运动的图像，物理学中把这种图像叫作“正弦曲线”（“余弦曲线”）。由此让学生对正弦函数（余弦函数）的图像有一个直观的印象。

教师再以问题驱动的方式引导学生利用单位圆上的点来画正弦函数的图像，引发学生的思考——

师刚才，我们观察了正弦曲线的样子。这节课，我们先来探究正弦函数图像的画法。请大家仔细观察硬纸板上的曲线形状，思考一下怎样在草稿纸上画出这样的图像。

生照样子随手画。

师随手画能保证画出来的图像精确吗？

生（众）不能。

师请同学们回忆一下，我们是怎么定义正弦函数的？

生利用单位圆上的点的坐标。

师没错。所以，我们先来尝试一下能否利用单位圆上的点画出精确的正弦函数图像。

（二）技术融合，突破难点

教师利用GeoGebra软件展示：将单位圆分成12等份，以x轴为始边，可以得到13個终边不同的圆心角，它们的大小分别为0、π6、π3、π2、2π3、5π6、π、7π6、4π3、3π2、5π3、11π6、2π。根据正弦函数的定义，这些角的终边与单位圆的交点的纵坐标就是它们所对应的正弦值。把x轴上0到2π这一段分成12等份，以上述13个圆心角的大小为横坐标，以它们的终边与单位圆的交点的纵坐标为纵坐标，在平面直角坐标系中画点（如图2）。引导学生观察画出的这13个点，并思考：若以其他的圆心角的大小为横坐标，以其终边与单位圆的交点的纵坐标为纵坐标画点，那么这些新画出的点在什么位置？

接着，教师使用GeoGebra软件画出完整图像。具体操作步骤如下：打开GeoGebra软件，画点O（0，0）、A（1，0）并锁定对象。以O为圆心，以A为圆周上一点画单位圆，取单位圆上的任意一点B。以O为圆心，以A为起点，以B为终点画圆弧，记弧长为d。输入指令“（d，y（B））”，记为点D。过点D作x轴的垂线段，并连接OB、BD，跟踪点D，启动点B动画。这些点构成了正弦函数在0到2π范围内的图像（如图3）。

通过此探究活动，学生能够知道利用单位圆能够画出0到2π范围内精确的正弦函数图像，并体会正弦函数图像与正弦函数定义之间的内在逻辑联系。

教师进一步引导学生思考整个定义域R内正弦函数的图像——

师我们已经得到了正弦函数y=sinx在[0，2π]范围内的图像，请同学们结合前几节课的内容，思考怎么作出y=sinx在整个定义域R内的图像。

生将[0，2π]范围内的图像平移。

师很好！你的依据是什么？

生终边相同的角的三角函数值相同。

师没错。所以，函数y=sinx，x∈[2kπ，2（k+1）π]，k∈Z且k≠0的图像与函数y=sinx，x∈[0，2π]的图像一致。因此，只要将正弦函数在[0，2π]范围内的图像不断向左、向右平移，每次移动2π个单位长度，就能得到正弦函数在整个定义域R内的图像了。我们一起来看一下动态效果。

（三）化繁为简，抓住五点

本环节以问题驱动教学过程，并结合波利亚的解题四步骤解决问题——

（1）弄清问题。教师提问：虽然利用单位圆上的点能够画出正弦函数y=sinx，x∈[0，2π]的图像，但是比较麻烦，那么，是否有更方便的办法画出其简图呢？

（2）拟定计划。学生思考：能否通过几个特殊的圆心角大小及其终边与单位圆的交点的纵坐标来确定正弦函数图像上的几个点，用光滑的曲线连接这些点，从而画出正弦函数的简图？以小组为单位进行讨论，共同拟定计划，确定想选择哪几个特殊的圆心角。

（3）实现计划。各小组成员在思考和讨论后，根据拟定的方案在草稿纸上画出正弦函数y=sinx，x∈[0，2π]的简图。然后，各小组代表依次向全班同学解释画y=sinx，x∈[0，2π]的简图可选取哪几个特殊的圆心角，并展示其作品。教师对小组汇报结果进行评价与指导、补充。

（4）回顾讨论。教师带领学生回顾画出来的正弦函数y=sinx，x∈[0，2π]的简图，讨论画简图时哪些点最关键，从而总结画简图的一般方法——五点作图法，并在黑板上具体画出相应的简图。

（四）变式迁移，巩固提升

教师要求学生将总结出的正弦函数的“五点作图法”迁移运用到余弦函数或其他可由正弦函数变换得到的函数的作图问题中，加深学生对作图步骤以及“五点作图法”的理解，帮助学生学会举一反三。

此环节让学生在一些变式问题中运用学到的知识，有利于学生通过一个特殊的函数（正弦函数）明白作简图的方法，从而掌握一类函数作简图的方法，以此完成知识的迁移。

变式问题可以设计为：

（1）你能以正弦函数的图像为基础，通过平移变换得到余弦函数的图像吗？你能运用已经学过的三角函数的诱导公式解释其中的原理吗？

（2）不通过平移变换，只运用“五点作图法”，你能类比画出余弦函数在[0，2π]范围内的简图吗？在画余弦函数的简图时，应抓住哪几个关键点？

（3）根据“列表—描点—连线”的步骤，运用“五点作图法”画出y=1+sinx，x∈[0，2π]的图像与y=-cosx，x∈[0，2π]的图像。

（4）小组讨论“五点作图法”是否可以运用到函数y=Asin（ωx+φ）上。如果可以，在画简图时，应选择哪五个点作为关键点？

（五）拓展应用，数据拟合

教师播放、学生观看“为了测量重力加速度，运用Tracker软件自动跟踪摆球位移，并实时记录位移（水平位移与垂直位移）与时间数据”的视频（图4为一个瞬间），探讨硬纸板上的“正弦曲线”（“余弦曲线”）的物理意义：是否代表漏斗摆动时离开平衡位置的位移与时间的函数图像？

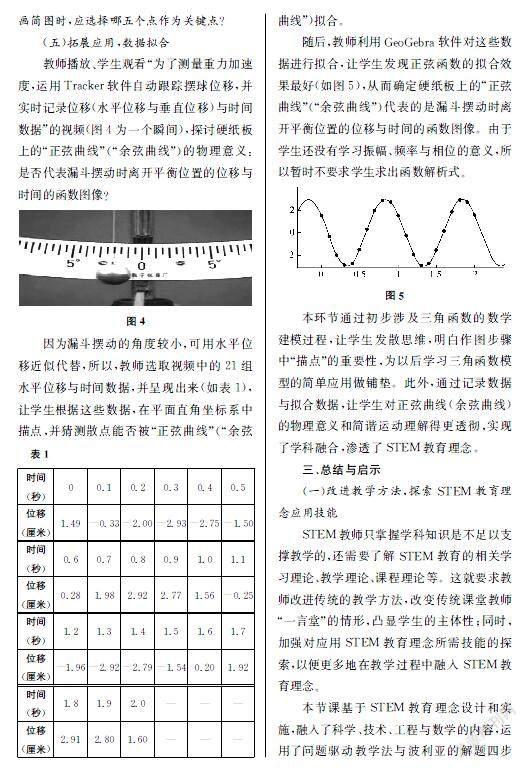
因为漏斗摆动的角度较小，可用水平位移近似代替，所以，教师选取视频中的21组水平位移与时间数据，并呈现出来（如表1），让学生根据这些数据，在平面直角坐标系中描点，并猜测散点能否被“正弦曲线”（“余弦

随后，教师利用GeoGebra软件对这些数据进行拟合，让学生发现正弦函数的拟合效果最好（如图5），从而确定硬纸板上的“正弦曲线”（“余弦曲线”）代表的是漏斗摆动时离开平衡位置的位移与时间的函数图像。由于学生还没有学习振幅、频率与相位的意义，所以暂时不要求学生求出函数解析式。

本环节通过初步涉及三角函数的数学建模过程，让学生发散思维，明白作图步骤中“描点”的重要性，为以后学习三角函数模型的简单应用做铺垫。此外，通过记录数据与拟合数据，让学生对正弦曲线（余弦曲线）的物理意义和简谐运动理解得更透彻，实现了学科融合，渗透了STEM教育理念。

三、总结与启示

（一）改进教学方法，探索STEM教育理念应用技能

STEM教师只掌握学科知识是不足以支撑教学的，还需要了解STEM教育的相关学习理论、教学理论、课程理论等。这就要求教师改进传统的教学方法，改变传统课堂教师“一言堂”的情形，凸显学生的主体性;同时，加强对应用STEM教育理念所需技能的探索，以便更多地在教学过程中融入STEM教育理念。

本节课基于STEM教育理念设计和实施，融入了科学、技术、工程与数学的内容，运用了问题驱动教学法与波利亚的解题四步骤。由此，我们认为，教师应用STEM教育理念时需要具备的技能包括但不限于对学科知识的深入理解、对科学情境与学科知识交叉融合点的挖掘、对信息技术（如某些软件）的熟练使用以及一定的工程设计能力。

（二）反馈教学情况，凸显STEM教育理念应用效果

STEM教育应该注意学生能否高效地学到知识或技能。遇到结果难以评价的情况时，教师应该变换评价方式，积极地从面向过程的评测中检验STEM教育的质量。因此，在本节课中，为了凸显基于STEM教育理念的教学效果，我们采用多元化的评价方式，通过经常跟学生互动来了解学生的学习情况，并且让学生以小组汇报的形式解释相关问题，得到教学情况的实时反馈。

（三）反思教学过程，探究STEM教育理念应用模式

本节课，在引出“正弦函数的图像”这一课题时，以简谐运动为背景，交叉融合了物理知识;在探究单位圆与正弦函数图像之间的联系时，融入了技术手段，使用了动态数学软件GeoGebra;在考虑是否有更简便的方法画正弦函数在[0，2π]范围内的简图时，聚焦于问题的解决并且运用了波利亚的解题四步骤;而在引入與探究环节，都设计了动手操作活动，帮助学生体验知识的形成过程。因此，我们认为，应用STEM教育理念进行数学教学的模式的关键在于“跨学科”“使用技术”“问题解决”以及“动手操作”。

本文系教育部人文社会科学研究青年基金项目“创新型STEM教师培养的探索性研究”（批准号：18YJC880115）的阶段性研究成果。

参考文献：

[1] 袁智强.交叉融合的STEM教育：背景、内涵与展望[J].教育研究与评论（中学教育教学），2019（3）.

[2] 曾宁，张宝辉，王群利.近十年国内外STEM教育研究的对比分析——基于内容分析法[J].现代远距离教育，2018（5）.

[3] 吴志强.STEM教育理念下的生物教学[J].教育研究与评论（中学教育教学），2018（10）.

[4] 梅浩，袁智强，郑柯.基于数学实验的STEM教育——以“探究金属的冷却模型”为例[J].教育研究与评论（中学教育教学），2019（3）.

[5] 逯行，李子运，李芒.国内整合学科的STEM教育教师专业发展研究[J].数字教育，2018（3）.

[6] 宋怡，马宏佳，祁宇.STEM教育愿景中的课程、教学与评价——基于美国《STEM2026：STEM教育创新愿景》报告[J].现代教育科学，2017（11）.