慢下脚步，倾听同伴

朱国荣

摘要：每一次学习，就像一场旅行，在乎的不只是目的地，还有沿途的风景和陪你看风景的人。在关键处慢下脚步，倾听同伴的声音，理解他人的表达，认同观点，内化概念，质疑问题，厘清错误，才能更好地理解数学的内涵，感悟学习的意义。以《倍的认识》一课为例，说明数学教学应该在美丽风景处，在前行的岔路口，在看不清、看不透的地方慢下脚步。

关键词：数学教学放慢倾听倍的认识

每一次学习，就像一场旅行，在乎的不只是目的地，还有沿途的风景和陪你看风景的人。

数学课程内容不仅包括数学的结果，也包括数学结果的形成过程和其中蕴含的数学思想方法。每一次学习之旅，我们不能只将获得数学的结果当作目的地;经历数学结果的形成过程、感悟其中蕴含的数学思想方法，都是重要的目标，都是沿途美丽的风景。每一次学习之旅，每一位学生都不是独行者，教师和同伴都是陪他一起看风景的人。在关键处慢下脚步，倾听同伴的声音，理解他人的表达，认同观点，内化概念，质疑问题，厘清错误，才能更好地理解数学的内涵，感悟学习的意义。

一、在美丽风景处慢下脚步

面对未知的数学内容，面对富有挑战性的学习任务，每一位学生都会情不自禁地投入其中，自主探索，合作交流，不同的认识和理解自然生成。在这美妙的、让人怦然心动的时刻，观点的碰撞悄然展开。这时，需要慢下脚步，倾听同伴的声音。

这是《倍的认识》一课的教学场景。教师在黑板上贴出了两行图片：第一行2个圆，第二行4个三角形（如下页图1）。要求学生观察、比较圆的个数和三角形的个数，并交流“你发现了什么”。

图1

学生踊跃地表达了自己的发现：（1）三角形比圆多2个，圆比三角形少2个;（2）圆再加2个就和三角形一样多;（3）三角形是圆的1倍;（4）圆有2个，三角形比圆多1倍。

交流的过程中，学生对这四种说法都表示了赞同。显然，学生对倍的概念的前认知出现了偏差。于是，教师追问学生：“三角形是圆的1倍，你是怎么想的？”并请学生在图中圈一圈，更加清楚地表示出自己的想法。一位学生上台展示了圈画过程（结果如图2所示）。

图2

通过实际的圈画和直观的图示，学生明白第（3）个说法实际想表达的意思是：多出来的这2个三角形是圆的1倍。

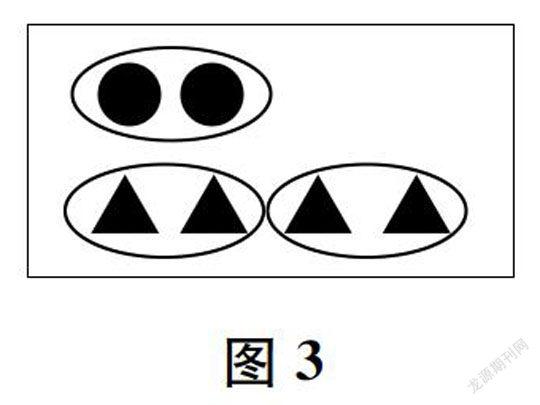
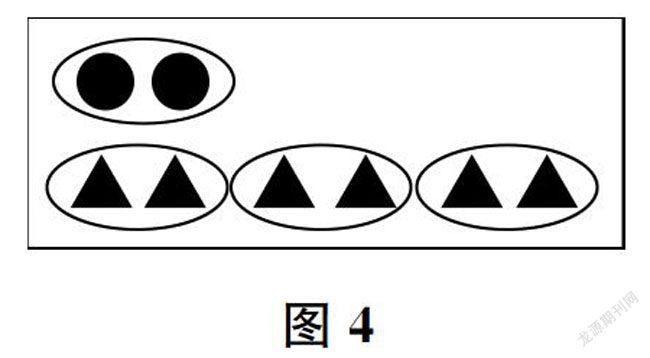
此时，教师继续在图中圈画（如图3），并且增加三角形（如图4），适时追问：“三角形的总個数是圆的个数的几倍？如果再增加2个三角形，那么三角形的总个数是圆的个数的几倍？”

图3

图4

通过交流，学生不但初步掌握了倍的概念，而且厘清了“多1倍”和“是2倍”、“多2倍”和“是3倍”的联系与区别，从而看到了更美的风景。

二、在前行的岔路口慢下脚步

面对同样的学习任务，不同的学生会产生不同的理解。有时，这些理解都是正确的，只是看问题的角度和思路不同;有时，则在思考的方向、方法上出现了偏差，产生了错误。无论不同，还是偏差，甚至错误，都是学习之旅中美丽的风景，都值得教师和学生慢下脚步，倾听、思考、表达、争论，让认识更加清晰，让感悟更加深刻。

还是那节《倍的认识》课上，第一个练习环节，教师呈现了图5—图7，要求学生思考：“三角形的个数是圆的个数的2倍吗？如果是，圈一圈;如果不是，改一改。”

图5

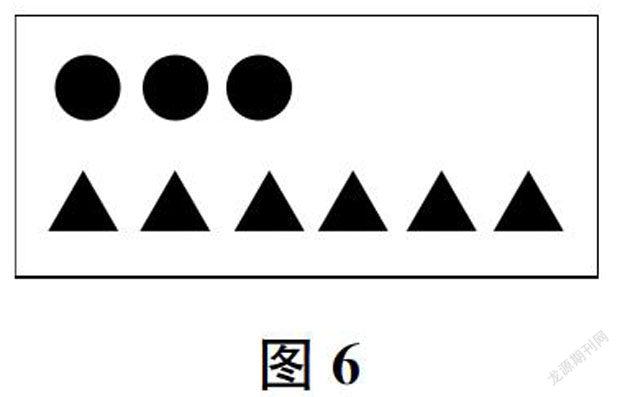
图6

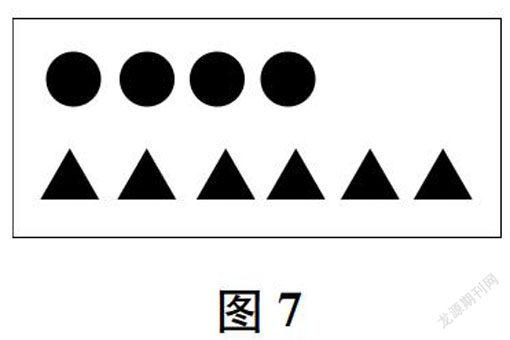
图7

对图5、图6，学生很快达成了共识：圆是1份，三角形有这样的2份，那么，三角形的个数就是圆的个数的2倍。

对图7，学生表达了不同的改法：（1）增加2个三角形;（2）减少1个圆;（3）增加8个圆。

三种改法，是学生解决问题的三种不同的思路，有直有曲。这时，教师需要引导学生慢下脚步，辨一辨，让学生看透风景。

通过讨论，学生认识到“增加2个三角形”和“减少1个圆”都是正确的，从而进一步加深了对“2倍关系”的理解和认知。遗憾的是，实际教学时，当一个学生表达可以“增加8个圆”时，教师追问：“增加8个圆，对吗？”在个别学生否定应答后，教师就一带而过了。

课后研讨时，问及授课教师“为何如此匆忙”，教师表达了两层意思：一是备课时，没有预设到这种回答，教学时，一下子不知道怎样应对;二是担心如果此处展开讨论，后面的内容就来不及教学了。显然，我们的教学还不够淡定和从容。当学生出现错误的表达时，我们不应该简单地否定了之，而需要引导学生慢下脚步，听明白其中的问题所在，通过讨论，厘清错误原因，找到合理之处。比如，可以呈现如图8所示的变化结果，引导学生说一说倍数关系，让学生知道这幅图表达的是“圆的个数是三角形的个数的2倍”，是把三角形的个数看作“1份”，圆有“这样的2份”，从而让学生更加深刻地认识到表达“2倍关系”时，分清“把谁看作1份”十分重要。

图8

三、在看不清、看不透的地方慢下脚步

真实的课堂上，学生会有各种各样的疑惑。教学中，教师要放慢脚步，鼓励学生主动将自己的疑惑（或者说是问题）提出来，展开讨论。当然，更为重要的是，教师需要深入开展对具体教学内容的研究，才能看到数学结果背后所蕴含的数学思想方法，才能更好地引导学生理解数学。

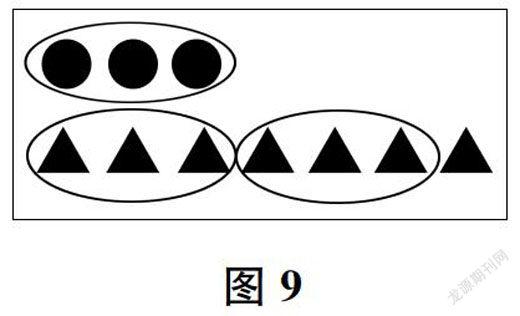
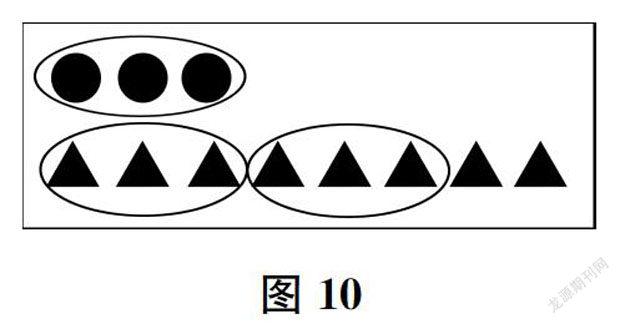
《倍的认识》一课，练习环节结束后，教师让学生停下学习的脚步，回顾这节课学习的内容，引导学生提出自己的困惑与问题。在这个环节，学生提出了一个非常有价值的问题：如果三角形的个数不正好是圆的个数的2倍，该怎么表示呢？这时，教师没有急于让学生发表意见，而是先引导学生厘清问题，通过交流，形成图9和图10，进而讨论得出“三角形的个数比圆的个数的2倍多1个（2个）”的表达方式，从而进一步丰富了学生对倍数关系的认识，完善了学生的认知结构。

图9

图10

临近下课时，教师整体呈现图5、图1、图6和图11，向学生提出了富有思考性的问题：“这四幅图中，三角形的个数和圆的个数之间的关系有什么相同的地方？有什么不同的地方？”

图11

经过思考和讨论，学生明白了“相差的个数不同”“倍数关系相同”，从而更加深刻地理解了“倍”这个新的数学概念。