驻波振幅极值法测量声速实验的误差分析

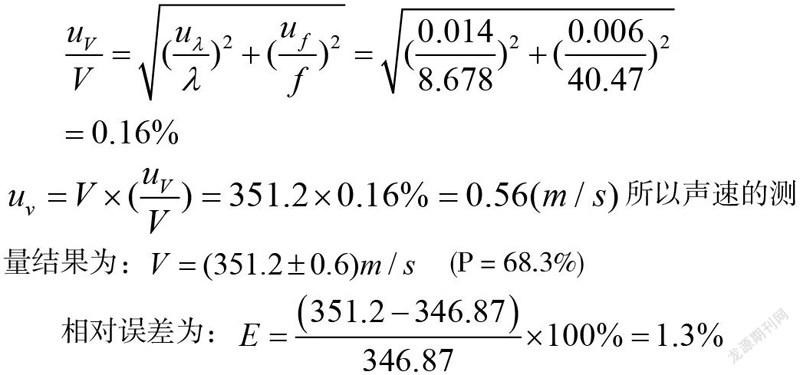
摘要：针对驻波振幅极值法测量声速实验的测量误差问题，计算了测量结果的不确定度和相对误差，分析了构成结果不确定度的主要因素和引起实验误差的可能来源，进一步指出了减小实验误差的方法，提高测量精度。

关键词：声速;驻波振幅极值法;误差;不确定度

声波是一种可在固、液、气态弹性媒介中传播的机械波。频率在20 kHz以上的短波长声波称为超声波，其具有定向好、功率大、穿透力强以及信息携带量大等突出优点，广泛应用于农业、工业、国防以及科学研究等领域，如超声波测距和定位、超声无损检测、流体测速、测量气体温度变化，以及测量材料的弹性模量等。关于声速的测量在声学应用技术领域尤为重要。其中，测量超声波在空气中的传播速度具有强的实际应用性和易于实现的特点，是经典的近代物理实验，成为许多高等院校大学物理实验教学中的基础实验项目[1， 2]。教学实验室主要采用驻波振幅极值法和相位比较法测量声速。两者相比较之，在驻波振幅极值法测量过程中，更易产生较大的观察偏差[3，4]，因此，本文主要对驻波振幅极值法测量声速实验进行误差分析，并指出减小实验误差的方法。

1实验原理

1.1声波在空气中的传播速度

声波在理想气体中的传播可视为绝热过程，声速V与气体的关系式为[5]：

式中，为气体的比热容比，定义为气体定压比热容与定容比热容的比值，即;R为摩尔气体常量，R = 8.314 J/（mol‧K）;是气体的摩尔质量;T是气体的热力学温度，相对于摄氏温度t，T = T0 + t，其中T0= 273.15 K。相应地，0℃时，声速V0 = 331.45 m/s。忽略大气压和水蒸气的影响，将空气近似看作理想气体，室温 t 摄氏度下的声速为[2， 5]：（2）

1.2 声波传播特点

在波动过程中，波的传播速度V与自身的频率f和波长λ的关系为：

因此，实验测出频率f和波长λ即可计算得到声速V。对于振动方向、频率相同，初相位差恒定，且传播方向相反的两列平面简谐波相遇而发生叠加，形成合成声波，其声压随空间位置不同呈极大值和极小值分布，这样的现象称为驻波现象[5]。驻波方程表达式为，其中合振幅分布2Acos2πx/λ与位置有关，相位cos2πvt与时间相关。由此可知，在满足的位置点，合振幅最大，称为波腹，此时， （n = 0， 1，2，3ˑˑˑ）;在满足的位置点，合振幅最小，称为波节，此时，。则相邻两个波腹或波节之间的距离。利用机械波传播的驻波现象，设计实验测出合成声波的声压中相邻两个波腹的距离即可计算出声波波长λ。

1.3驻波振幅极值法测量声速

利用主要由压电陶瓷片构成的超声声速测定仪发射和接收超声波，实验装置如下图1所示。通过函数信号发生器将激励电信号输入到超声声速测定仪的换能器（压电陶瓷片）S1上，调节信号源的输出频率为换能器S1的谐振频率 f0，S1端面发生机械振动，产生平面超声波，在空气中传播到换能器S2，经S2端面反射形成反射波。入射波与反射波在S1、 S2间相遇叠加，形成驻波，换能器S2将声压转化为电压，经由示波器监测驻波声压振幅随S1与S2的距离ln的周期性变化。声波的传播发生半波衰减，驻波声压的振幅随波源与接收器距离l的增加而衰减，当ln等于超声波半波长λ/2的整数倍时，驻波振幅达到极大值，如下图2所示。测量第1个和第n+1个声压极大值的距离ln，λ = 2ln/n，声速V = λf = 2fln/n[5]。

2实验内容及误差分析

2.1 实验内容

（1）预置函数信号发生器频率为 40 kHz、电压幅度为 10 V。微调信号发生器输出的正弦波频率为超声声速测定仪的谐振频率f0，使示波器呈现的正弦信号振幅达到最大，确定该值为实验超声波的频率。

（2）转动读数鼓轮，逐渐拉开S2，每移动一次半波长λ/2距离出现一次声压极大值，连续测量12个极大值数据l1… l12。采用逐差法进行数据处理，求出波长平均值和声速，计算测量结果的不确定度和相对误差。

（3）计算实验室室温t下的声速理论值，求实验相对误差。

2.2 实验结果分析

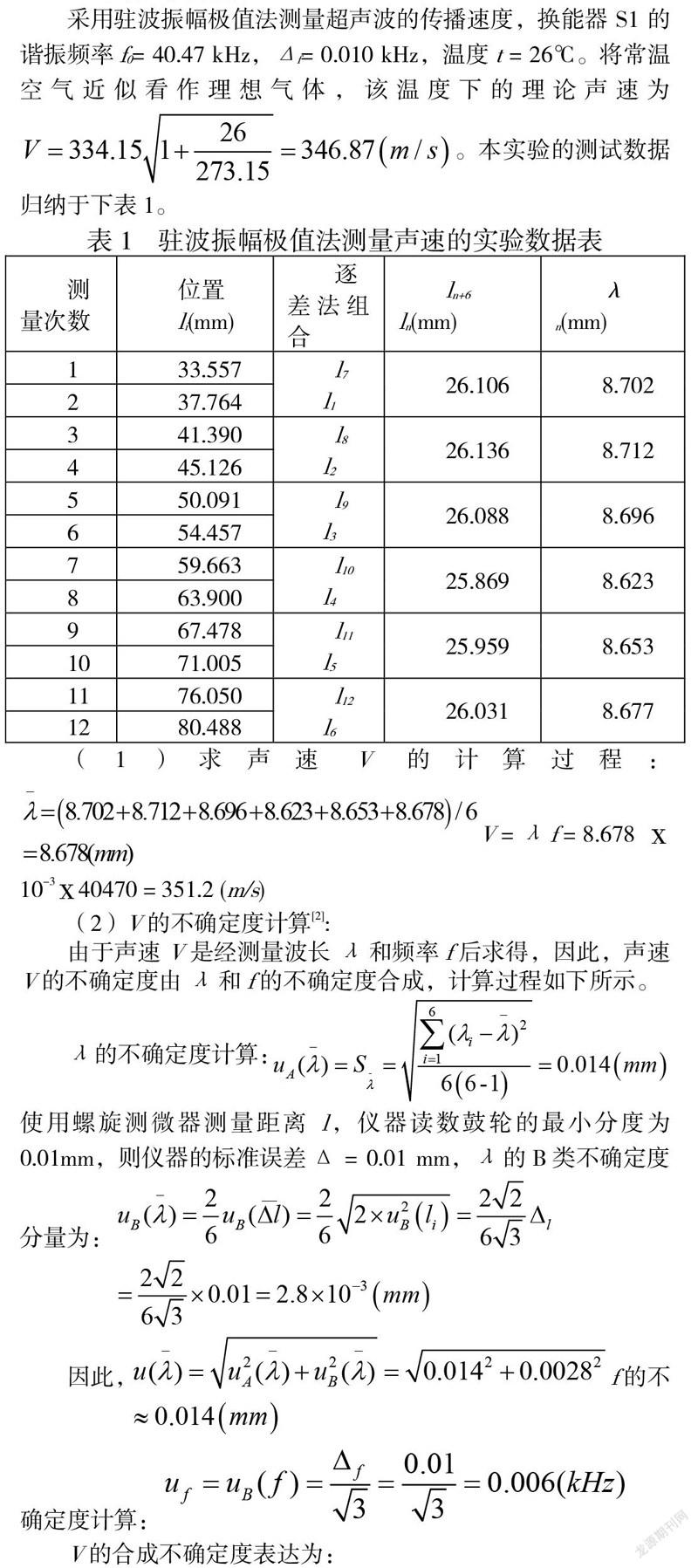
采用驻波振幅极值法测量超声波的传播速度，换能器S1的谐振频率f0= 40.47 kHz，Δf= 0.010 kHz，温度t = 26℃。将常温空气近似看作理想气体，该温度下的理论声速为。本实验的测试数据归纳于下表1。

（1）求声速V的计算过程：V = λ f = 8.678 ⅹ10-3ⅹ40470 = 351.2 （m/s）

（2）V的不确定度计算[2]：

由于声速V是经测量波长λ和频率f后求得，因此，声速V的不确定度由λ和f的不确定度合成，计算过程如下所示。

λ的不确定度计算：使用螺旋測微器测量距离l，仪器读数鼓轮的最小分度为0.01mm，则仪器的标准误差Δ = 0.01 mm，λ的B类不确定度分量为：

因此，f的不确定度计算：

V的合成不确定度表达为：

所以声速的测量结果为： （P = 68.3%）

相对误差为：

2.3误差分析

根据声速V的合成不确定度uv可知，uv由波长λ分量不确定度uλ和频率 f分量不确定度uf构成，并且uλ的贡献最大，这说明，测量λ时读数l的重复性引起主要的测量结果不确定度。结合实验条件，驻波振幅极值法测量声速的测量误差主要源于驻波场的偏离、波长λ的测量误差、谐振频率 f的确定误差以及实验环境影响等方面[3， 6]。具体分析如下：

（1）偏离严格的驻波场。

超声波在空气中的传播，处于近场区时并不以简谐波传播，声压振幅无严格的周期性规律特征;当传播至10cm以上的远场区，超声波以简谐波传播，经由反射叠加形成驻波。声速测量仪的两个换能器端面间的最大距离约20cm，实际实验操作在两换能器间距大于4cm后开始记录数据，因而，由换能器发射的超声波并非全程以简谐波传播，经反射叠加也并非形成标准的驻波场。非标准的驻波场导致了在不同区间测得振幅的两个相邻极大值的间距λ/2不同，使得测量结果产生较大误差。另外，接受换能器作为反射端面，也产生散射，激起散射波，影响超声波入射波与反射波的叠加。

（2）波长λ的测量误差。

转动螺旋测微器的鼓轮调节声速测量仪两个换能器间的距离，记录声压振幅出现极大值时换能器S2的位置，但对这样特殊位置的确定易发生判断偏差，引入人为误差。

（3）谐振频率 f的确定误差。

调节正弦波输出频率等于超声换能器S1的谐振平率f0，示波器呈现的声压电压达到最大。尽管正弦波频率不等于谐振频率f0時，超声声速测量仪的声波发射器与接收器的间距是半波长整数倍时，声压振幅也达到最大值，这一现象易引起调节谐振频率f0时的判断错误，造成结果误差。

（4）实验环境带来的误差。

在教学实验中，学生人数较多且实验操作时间长，实验者的走动和呼吸、实验台的振动等均影响空气密度，影响声波在空气中的传播，引起误差。另外，将实验室空气视为理想气体，计算声速理论值亦引入误差。

3 减小误差的方法

结合上述误差来源的分析和实验条件，根据驻波振幅极值随位置呈周期性分布的特性，提出以下可能的改进方法，从而提高实验测量精度。

（1）增加声速测量仪两个压电换能器间的距离，以满足超声波以简谐波传播，与反射波形成标准的驻波场，尽可能使任一区间的两个相邻驻波极大值的间距λ/2为一固定常数，与测量位置无关。

（2）将声波反射面改用为面积较大的硬质材料，提高反射率和降低散射，减小散射对驻波场的影响。

（3）调节正弦波输出频率f接近声速测量仪换能器的谐振频率f0时，使示波器呈现的声压振幅达到极大值，记录此时输出频率f。同时，增加两个换能器间的距离，若观察到电压信号继续增加至最大值，说明，此前的正弦波输出频率f为发射换能

器的谐振频率f0，不是驻波在某距离下的共振干涉频率[4]。

（4）为减少实验环境的空气密度变化，实验测量过程中，要求操作者身体不触碰实验操作台，减少不必要的走动，保持安静。

4结论

本文针对驻波振幅极值法测量声速实验的测量误差，从声速V不确定度的组成确定测量l重复性是引起结果不确定度的主要来源，进一步从非标准驻波场、测量l的人为判断误差、谐振频率f0的确定以及实验环境等方面分析对测量结果造成影响的可能原因，也指出了减小误差的方法，提高实验测量精度。

参考文献：

[1]曹正东，刘钟毅，袁伟等.大学物理实验[M].上海：同济大学出版社，2003年.

[2]陈国杰，李斌，谢嘉宁等.大学物理实验[M].北京：科学出版社.2002年.

[3]冯登勇，王昆林.声速测定实验不确定度、误差之比较研究 [J].大学物理实验，2014，（1）：88-91.

[4]陈中钧.超声波声速测量实验中的误差分析[J].实验科学与技术，2005（10）：145-147.

[5]周克省，赵新闻，甘咏梅等.大学物理[M].湖南：中南大学出版社.2008年.

[6]上官经邦， 陈新华， 黄海宁等. 水下声学定位系统及其误差分析[J].网络新媒体技术，2016，5（3）：27-36.

资助项目：

2019年佛山科学技术学院高层次人才科研启动项目“过渡金属离子Mn4+掺杂氟化物窄带红光材料的合成、结构及其器件应用研究”。

作者简介：

邓婷婷（1989-），女，广东茂名人，佛山科学技术学院讲师，博士，从事大学物理实验教学、光源与照明专业相关课程教学和研究。