新课程理念下培养学生的创新思维能力之我见

吴宗流

摘要：随着新一轮基础教育改革的持续推进，新课程今秋全面登陆我市，加强数学学习思维的研究，不仅有利提高课堂教学质量和效率，还有利于学生的可持续发展。提高中学数学教学质量，不仅仅是为了提高学生的数学成绩，更重要的是能使学生学到有用的数学，全面推进素质教育，而素质教育的核心是培养学生的创新能力，本文结合教学实际，谈谈如何利用课堂教学的功能，培养学生的创新思维，从而提高创新的能力。

关键词：新课程;建模;创新思维;创新能力

在诸多的思维活动中，创新思维是最高层次的思维活动，是开拓性、创造性人才所必须具备的能力。麻省理工大学创新中心提出的培养创造性思维能力，主要应培养学生灵活运用基本理论解决实际问题的能力。由此，我认为培养学生创造性思维的过程有三点基本要求。第一，对周围的事物要有积极的态度;第二，要敢于提出问题;第三，善于联想，善于理论联系实际。因此在数学教学中构建学生的建模意识实质上是培养学生的创造性思维能力，因为建模活动本身就是一项创造性的思维活动。它既具有一定的理论性又具有较大的实践性;既要求思维的数量，还要求思维的深刻性和灵活性，而且在建模活动过程中，能培养学生独立，自觉地运用所给问题的条件，寻求解决问题的最佳方法和途径，可以培养学生的想象能力，直觉思维、猜测、转换、构造等能力。而这些数学能力正是创造性思维所具有的最基本的特征。

一、发挥学生的想象能力，培养学生的直觉思维

众所周知，数学史上不少的数学发现来源于直觉思維，如笛卡尔坐标系、费尔马大定理、歌德巴赫猜想、欧拉定理等，应该说它们不是任何逻辑思维的产物，而是数学家通过观察、比较、领悟、突发灵感发现的。通过数学建模教学，使学生有独到的见解和与众不同的思考方法，如善于发现问题，沟通各类知识之间的内在联系等是培养学生创新思维的核心。

例：证明

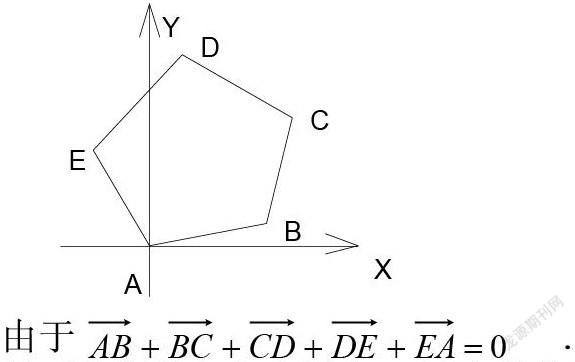
分析：此题若作为“三角”问题来处理，当然也可以证出来，但从题中的数量特征来看，发现这些角都依次相差72°，联想到正五边形的内角关系，由此构造一个正五边形（如图）

从而它们的各个向量在Y轴上的分量之和亦为0，故知原式成立。

这里，正五边形作为建模的对象恰到好处地体现了题中角度的数量特征。反映了学生敏锐的观察能力与想象能力。如果没有一定的建模训练，是很难“创造”出如此简洁、优美的证明的。正如E·L泰勒指出的“具有丰富知识和经验的人，比只有一种知识和经验的人更容易产生新的联想和独创的见解”。

二、构建建模意识，培养学生的转换能力

恩格斯曾说过：“由一种形式转化为另一种形式不是无聊的游戏而是数学的杠杆，如果没有它，就不能走很远。”由于数学建模就是把实际问题转换成数学问题，因此如果我们在数学教学中注重转化，用好这根有力的杠杆，对培养学生思维品质的灵活性、创造性及开发智力、培养能力、提高解题速度是十分有益的。

如在教学中，我曾给学生介绍过“洗衣问题”：

给你一桶水，洗一件衣服，如果我们直接将衣服放入水中就洗;或是将水分成相同的两份，先在其中一份中洗涤，然后在另一份中清一下，哪种洗法效果好？答案不言而喻，但如何从数学角度去解释这个问题呢？

我们借助于溶液的浓度的概念，把衣服上残留的脏物看成溶质，设那桶水的体积为x，衣服的体积为y，而衣服上脏物的体积为z，当然z应非常小与x、y比可忽略不计。

第一种洗法中，衣服上残留的脏物为 ;

按第二种洗法：第一次洗后衣服上残留的脏物为 ;第二次洗后衣服上残留的脏物为 ;显然有这就证明了第二种洗法效果好一些。

事实上，这个问题可以更引申一步，如果把洗衣过程分为k步（k给定）则怎样分才能使洗涤效果最佳？

学生对这个问题的进一步研究，无疑会激发其学习数学的主动性，且能开拓学生创造性思维能力，养成善于发现问题，独立思考的习惯。

三、加强创新意识的培养

创新意识是创新精神的主体，是创新能力的心理基础。加强对学生创新意识的培养是培养学生创新能力的关键。

（1）要求学生不迷信、不盲从，不把任何自己没有明确认识为真的事物当成真的加以接受鼓励质疑。

（2）有问必答。对学生提出的问题一定要回答，哪怕再简单，哪怕回答委婉些或留有余地。这主要是鼓励学生有勇气提出自己的问题，哪怕很简单，这至少说明他在思考。也只有学生积极思考了，才有创新的可能性。

（3）有意设疑。“答疑不答，贵在启发”，这是教学答疑的一个技巧。教学中，学生提出的问题中的疑点和难点内容，绝不只讲是什么，有意设计一些疑问留给学生，启发他们探索，让学生在探索中增强创新意识。

四、以“构造”为载体，培养学生的创新能力

“一个好的数学家与一个蹩脚的数学家之间的差别，就在于前者有许多具体的例子，而后者则只有抽象的理论。”

我们前面讲到，“建模”就是构造模型，但模型的构造并不是一件容易的事，又需要有足够强的构造能力，而学生构造能力的提高则是学生创造性思维和创造能力的基础：创造性地使用已知条件，创造性地应用数学知识。

五、挖掘典型例（习）题，培养灵活思维

数学教学是学生创造性的活动过程，为了使学生获得真正的数学知识，在课堂教学中，教师应该充分挖掘典型例（习）题。通过一题多解，一题多变、一题多联的方法进行 训练，开拓解题思路，开阔视野，促使知识迁移，提高学生思维的灵活性和广阔性，也有利于创新意识与创新思维的培养。

创新思维能力的培养是素质教育的灵魂和核心，是推行素质教育的一个永久话题。只要我们在教学中教师仔细地观察，精心的设计，可以把一些较为抽象的问题，通过现象除去非本质的因素，从中构造出最基本的数学模型，使问题回到已知的数学知识领域，就能培养学生的创新能力，从而提高学生分析问题和解决问题的能力。

参考文献：

[1]古良浩.新课程理念下培养学生数学创新能力之我见[J].数学教学通讯，2006（04）：31-34.