复合匀质块排样方式及其生成算法

李华

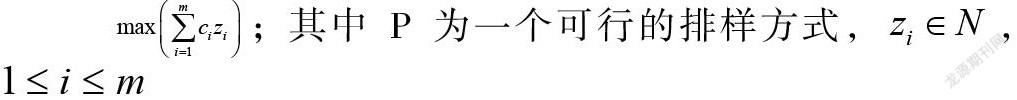
摘要：讨论矩形毛坯无约束的二维排样问题，提出了复合匀质块排样方式及其生成算法，算法设计简单。排样时通过枚举剪切线的位置，将板材分为两段，每段采用匀质条带规范排样方式及其动态规划算法生成条带最优布局。通过枚举法确定板材中段的最优组合，从而使板材的利用率达到最高。采用大量的例题测试，实验计算结果表明：使用复合匀质块排样方式及其生成算法在利用率和计算时间两方面均有效。

关键词：二维排样;枚举;动态规划;复合匀质块

0、引言

许多行业如制造业、木材加工业以及金属板或玻璃板的切割加工业等，都会涉及到材料的分割问题，而矩形零部件排样是制造行业经常涉及的问题。本文提出一种生成复合匀质块排样方式算法。实验结果表明，本算法在计算时间能够满足实际的需要同时，可有效的提高资源的利用率，且采用“一刀切”的切割工艺，与同形块两阶段排样方式相比，不会额外增加切割刀数，切割工艺较为简单。

1、排样问题的数学模型及相关概念

1.1数学模型

本文讨论矩形毛坯无约束的二维棑样问题（unconstrained two-dimensional cutting problems， UTDC）：采用剪切方式，将的板材切出种毛坯，每种毛坯在板材中出现的次数无约束，第种毛坯的尺寸大小为，价值为（），优化排样的目标是单张板材所含有的毛坯总价值达到最大。设可行的排样方式（排样图）中含有第种毛坯个，板材和毛坯的尺寸均为整数，为自然数的集合，UTDC的数学模型如下：

UTDC算法与二维下料问题密切相关。针对大规模下料问题，通常采用UTDC算法与线性规划相结合来求解。所谓二维矩形下料问题（Cutting Stock Problem）是指从已知尺寸的板材中切割出满足给定尺寸和需求量的一组不同规格矩形毛坯，并使得消耗的板材数达到最小。在确定棑样方案的过程中，要反复调用UTDC算法，生成排样方案中的一个或多个排样方式。因此，要求在合理的计算时间内，UTDC算法能给出高质量的解。

1.2相关概念

1.2.1 同质条带

同质条带是指一根条带中只含有尺寸和方向均相同的毛坯。同质条带分为水平条带或竖直条带，剪切时每一刀从板材上剪切一根水平（X向）或竖直（Y向）条带。

1.2.2 匀质块方式

匀质块的排样方式，由一组水平和竖直的同质条带组成。切割的过程分为两个阶段：首先对板材进行一系列条带切割，剪切时每一刀从板材切下一根水平（X向）或竖直（Y向）条带。然后，将条带切割成毛坯。

1.2.3 复合匀质块方式

复合匀质块是在匀质块的基础进行扩展，用枚举法确定剪切线的位置，将板材分为上下两个区域，用动态规划递推算法确定每个区域匀质块的排样最优布局。

2、算法原理及实现过程

2.1算法原理

动态规划是处理多阶段决策过程最优化的重要的方法，其目标是实现整个过程的整体效果最优。

2.2运用动态规划实现匀质块排样的价值

匀质块排样方式是一种剪切的排样方式，从板材上切下一根X或Y向条带，将条带分割成毛坯。排样过程是切割的逆过程，是条带拼接的过程，每次总是沿子板材的X向边或Y向边拼接上一根条带，最终形成段的最优布局。

递推思想：要从板块上切下一根同质条带，满足板块的所含毛坯总价值最大。为此需要考察所有条带，按价值最大的原则，选取所需拼接的X向或Y向条带。

2.3生成复合匀质块排样的价值

运用动态规划原理，求解一维背包问题，确定上下两段的最优组合，使板材所含毛坯的总价值达到最大。当板材水平放置时，Subject to：P采用匀质块排样方式，其中，为排样方式P含有的第种毛坯的数目，为自然数的集合。要求排放的毛坯互不重叠且不超过板材的边界。算法2为生成复合匀质块排样方式的算法。

其中，为板材所水平放置时所含毛坯的最大价值。通过枚举水平分割线的位置，将板材分为上下两段，然后，上下两段分别调用匀质块生成算法获取上下两段对应的匀质块的价值，将两者求和得到当前板材所含毛坯的总价值，若则更新的值，依次进行，最终确定板材的最优布局。

2.4板材复合匀质块排样方式算法设计思路

Step1 输入板材和毛坯的数据

Step2 结合枚举算法和动态规划递推算法，生成复合匀质块排样方式算法。

Step3将板材水平放置，调用复合匀质块排样方式生成算法，获取板材包含毛坯的最大价值。

Step4根据板材（水平或竖直放置时）的排样过程，反向追踪，获取复合匀质块排样方式中毛坯的最優布局。

3、实验计算结果

实验采用Pentium（R） Dual-Core CUP E5700，主频3.00GHz，内存2.0GB的计算机进行测试。

3.1 毛坯、板材方向固定

假定毛坯和方向固定的情况下，采用文献[3-4]中的50道例题作为实验数据，每题包含30种毛坯，板材的尺寸为，毛坯的长度和宽度均在内均匀分布，每种毛坯的单价等于其面积。用材料的利用率衡量排样方式的质量（它等于排样方式中所含毛坯的总面积与板材的面积之比）。

4、结束语

本文给出了枚举和递推技术相结合的复合匀质块排样算法，考虑了毛坯和板材方向固定以及同时旋转90°情况下，板材所含毛坯的最大价值，算法设计思想简单，在合理的计算时间内，提高了材料利用率。综合实际的应用需求，将本算法与线性规划相结合，可以求解矩形毛坯的下料问题。

参考文献：

[1]崔耀东.生成矩形毛坯最优T形排样方式的递归算法[J]. 计算机辅助设计与图形学学报.2006，18 （1）：125-127

[2]崔耀东，季君，曾窕俊.生成矩形毛坯最优两段排样方式的递归算法[J].南京航天航空大学学报.2006，38 （1）： 112-114.

[3][黄玲，崔耀东.矩形毛坯匀质条带排样方式及其生成算法 [J]. 桂林理工大学学报，2010，30 （2）：292-295]