产品最优求解问题中运筹学方法的应用

张青等

【关键词】运筹学；最优利润；最优产量；线性规划；动态规划；决策

“韩信点兵，多多益善”，“运筹”本意是算筹，后引伸为谋略，最早出于汉高祖刘邦对张良的一句评价：“运筹帷幄之中，决胜千里之外。”现代运筹学的起源可追溯到某些机构的管理中最先试用的科学手段 ，现在普遍认为，运筹学是从第二次世界上大战初期的军事任务开始的。所谓运筹学，是应用于数学的和形式科学的跨领域研究，利用统计学、数学模型等方法去寻找复杂问题的最佳答案。韩信点兵，并不仅仅是多多益善的问题，而更重要的却是“运筹帷幄”问题，否则将难以发挥一个组织系统的效率和作用。运筹学作为一门新兴科学，贯穿着效率和资源最优化的原则，在社会生活的广泛领域有着实用和科学的价值。对现实中的复杂问题，都可以用运筹学的方法进行解决，并改善和优化现有系统的效率。本文意图从运筹学在经济管理中的广泛运用这一方面出发，分析、论证其对经济管理系统进行定量分析和决策，以及对经济管理系统中人力、物力、财力等资源进行系统安排的过程，进而得出运筹学具有实现科学管理，为决策者提供最佳方案，取得最优经济效益的实效性和科学性的结论。

1 产品最优求解问题中运筹方法运用的一般步骤

在产品最优求解问题中，经常用到的是运筹学里的两个分支：线性规划和动态规划，用它们来求产品最优求解问题时的主要步骤如下：

1.1 在运用线性规划和单纯形法解决实际问题时建立数学模型一般有以下三个步骤：

（1） 提出来需要解决的问题并建立变量；

（2） 确定目标函数；

（3）分析问题所处的环境以及约束条件。

1.2 动态规划算法的基本步骤

设计一个标准的动态规划算法，通常可按以下几个步骤进行：

（1）分析最优解的性质，并刻画其结构特征。

（2）递归的定义最优解。

（3）以自底向上或自顶向下的记忆化方式计算出最优值。

（4）根据计算最优值时得到的信息，构造问题的最优解。

2 产品最优利润求解问题中运筹方法的运用

应用学科的科学性体现在其具备有效的科学方法上，运筹学在经济管理中的方法主要有线性规划。在经济管理中，线性规划是目前应用最广泛的、比较成熟的一种优化法，它经常运用在生产计划、物资调用、资源优化配置等方面。作为生产经营管理者，常常会遇到的这类问题：一是如何有效协调、解决劳动力、资金等资源条件之间矛盾，争取资源最大效益化；二是针对某一特定的工作目标时，如何合理组织生产，安排工艺流程，调整产品的成份，以使资源消耗最少。

例1：多品种多步骤产品最优利润求解模型研究

某生产车间生产甲、乙两种产品，每件产品都要经过两道工序，即在设备A和设备B上加工，但两种产品的单位利润却不相同。已知生产单位产品所需的有效时间（单位：小时）及利润见表1。问生产甲、乙两种产品各多少件，才能使所获利润最大。

分析：该问题所需确定的是甲、乙两种产品的产量，先建立其数学模型。

设x1，x2分别表示产品甲和产品乙的产量，x1，x2称为决策变量，根据问题所给的条件有

上述问题要确定的目标是：如何确定产量x1和x2，才能使所获利润为最大。利润的获取和x1，x2密切相关，以f表示利润，则得到一个线性函数式

所给问题的目标是要使线性函数f取得最大值，即目标函数是

以上是决策变量x1，x2受限的条件，把它们合起来称之为约束条件。

则本例的数学模型可归结为：

引入松驰变量x3，x4，将问题化为标准形式：

目标函数改写为

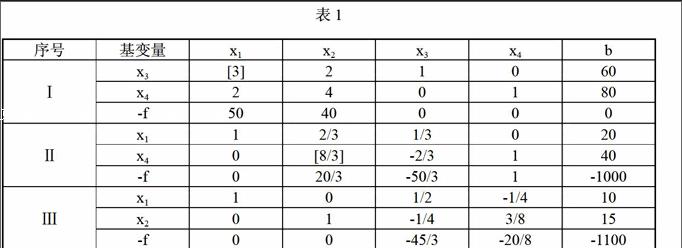
将约束条件的增广矩阵和改写后的目标函数的系数填入下表中，得到的表称为单纯形表：

因表1中检验数非正，得最优解，除去松驰变量后得；它表示：甲产品生产10件，乙产品生产15件时，最大利润为1100元。

3 产品最优产量求解问题中运筹放得运用

事物的发展往往复杂的、多变的，线性规划和单纯形法不能解决一些复杂问题，因此动态规划逐渐发展成为运筹学的一个分支。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。对于经济管理中法最短路线、资源分配、设备更新、库存管理、装载等问题，用动态规划方法可以很方便地求解。当然，动态规划也不是万能的，有它的局限性，适合用动态规划解决问题必须满足最优化原理和无后效性法的条件。

例2：不同产品负荷下最优产量动态规划研究

某工厂购进1000台机床，每台机床都可在高、低两种不同的负荷下进行生产，在高负荷下生产的产量函数为g（x）=10x（单位：百件），其中x为投入生产的机床数量，年完好率为；在低负荷下生产的产量函数为h（y）=6y（单位：百件），其中y为投人生产的机床数量，年完好率为b=0.9。计划连续使用5年，试问每年如何安排机床在高、低负荷下的生产计划，使在五年内生产的产品总产量达到最高。

分析：状态变量sk取为第k年度度初具有的完好机床台数。

决策变量xk为第k年度中分配在高负荷下生产的机器台数，则为第k年度中分配在低负荷下生产的机器台数（假定xk、sk皆为连续变量）。

状态转移方方程为：

第k年度的产量为：

最优值函数表示拥有机床数为sk时，从第k年度至第五年度采取最优分配方案进行生产时所获得的最大总产量。

则动态规划的基本方程为：

再从第5年度开始，用逆推归纳法进行计算。

计算结果表明：最优策略为

。

即头两年应该把年初全部机床投入低负荷生产，后三年应该把年初全部机床投入高负荷生产。这样会使产量最高，最高产量为29139百件产品。而且，从求解的过程中反过来就能确定每年年初的状态，即每年年初所拥有的完好机器台数。已知s1=1000，于是可得如下结论：第一年将1000台机器全部投入到低负荷下进行生产，第一年末机床完好数是900台，第二年将900台机器继续投入到低负荷下进行生产，第二年末机床完好数是810台，第三年将810台机床全部投入到高负荷下进行生产，第三年末机床完好数是567台，第四年将567台机床全部投入到高负荷下进行生产，第四年末机床完好数是397台，第五年将397台机床投入到高负荷下进行生产，这样第五年末剩下的完好机床数是278台，五年生产产品总数为29139（百件）。

随着科学和经济的发展和进步，运筹学也不断的发展完善成为近代应用数学的一个重要分支，它将生产经营中的一些难以解决的问题模型化，然后用运筹学的方法加以解决，为决策者提供定量、定性分析，帮助决策者做出最优决策。

参考文献

[1]何坚勇编著.运筹学基础[M].北京：清华大学出版社，2000.

[2]赵凤至，最优化计算方法.上海：上海科学技术出版社，1983.

[3]运筹学教材编写组.运筹学[M].北京：清华大学出版社，2005.