CO2膨胀体系混合物的黏度模型

张垚,贾秀璨,王晓坡

(西安交通大学热流科学与工程教育部重点实验室,710049,西安)

近年来,作为一种新型的绿色介质,气体膨胀液体在实际工业生产中越来越得到重视。气体膨胀液体是通过可压缩性气体(CO2、乙烷等)溶解到有机溶剂内形成的,其中CO2/有机溶剂膨胀体系(CXLs)被认为是应用最广泛的一种气体膨胀液体,主要应用在超临界流体分离、聚合物加工等方面[1-4]。当CO2气体溶解到液体中时,由于分子之间的相互作用有利于传质作用并降低液相黏度,因此开展这一类体系黏度的实验和理论研究对于其在工业中的实际应用具有重要的意义。

受气液溶解度变化的影响,且通常情况下CO2处于超临界状态,通过实验手段测量CO2膨胀体系的气液混合物黏度过程较为复杂,因此开展CO2膨胀液体黏度模型的研究就显得十分必要。通过调研发现,现有文献对CO2膨胀液体黏度模型的研究还不够深入,大部分研究仅停留在对实验数据的简单拟合方面。如Tomida和Ahosseini等通过Grunberg-Nissan方程对CO2与离子液体组成的混合物黏度数据进行关联[5-6],Jalili等通过修正的Setchenow方程对CO2/环丁砜的混合物黏度进行了计算[7],Matsuda等选择ASOG-VISO和McAllister三体模型对CO2膨胀液体的黏度数据进行关联[8]。

本文对Eyring-NRTL黏度模型进行了改进,建立了适用于CO2膨胀体系混合物的黏度模型,通过分析方程参数和气液配比的对应关系,确定了新的交互参数混合法则,提高了模型计算精度。

1 黏度理论模型的建立

2003年,Novak将Eyring绝对速率理论黏度模型与NRTL活度系数模型结合,提出了针对混合物的Eyring-NRTL黏度模型[9],其表达式为

lnη=x1lnη1+x2lnη2+

(1)

式中:x1和x2分别表示混合物中气相和液相的摩尔分数;η1和η2分别表示气相和液相的黏度;G12和G21分别表示二元混合物内部交互作用的吉布斯自由能

G12=exp(-ατ12)

(2)

G21=exp(-ατ21)

(3)

其中α为可调参数,一般设定为0.2,τ12和τ21为混合物二元交互作用参数,可表示为

τ12=g12-g22

(4)

τ21=g21-g11

(5)

g12、g22、g21、g11可以通过文献数据回归得到。

由于CO2膨胀液体为二元混合物,随着CO2摩尔分数的增加,混合物黏度逐渐减小,因此,本文认为Eyring-NRTL黏度模型中的二元交互作用参数与混合物平均摩尔质量M12之间可能存在一定的联系。鉴于此,在对大量实验数据分析的基础上,本文提出了如下关系式来表示二元作用参数

(6)

式中:ΔY表示τ12或τ21;p、p1、p2均为方程的系数。

混合物平均摩尔质量与各纯质的摩尔质量的关系可用下式表示

M12=x1M1+x2M2

(7)

2 模型计算结果与分析

本文首先对已发表文献中的CO2膨胀体系混合物的黏度进行了搜集整理,获得了CO2/正癸烷、CO2/正十四烷、CO2/正十八烷、CO2/甲醇、CO2/乙醇、CO2/丙醇、CO2/丙酮等7种混合物的黏度值[10-17],共计300个相关数据点。表1和表2分别给出了7种混合物黏度的相关数据以及通过改进的Eyring-NRTL黏度模型回归得到的参数。

图1和图2分别以CO2/乙醇溶液、CO2/丙酮溶液为例,给出了不同温度下文献黏度数据与本文模型计算值的比较。从图中可以看出,计算值和文献值吻合较好。图3给出了本文计算值与文献值的偏差分布。表3给出了本文改进后的Eyring-NRTL黏度模型计算值与文献值的绝对平均偏差δARD,其计算式为

(8)

图1 不同温度下CO2/乙醇溶液的黏度文献值[16]与本文计算值的对比

图2 不同温度下CO2/丙酮溶液的黏度文献值[15]与本文计算值的对比

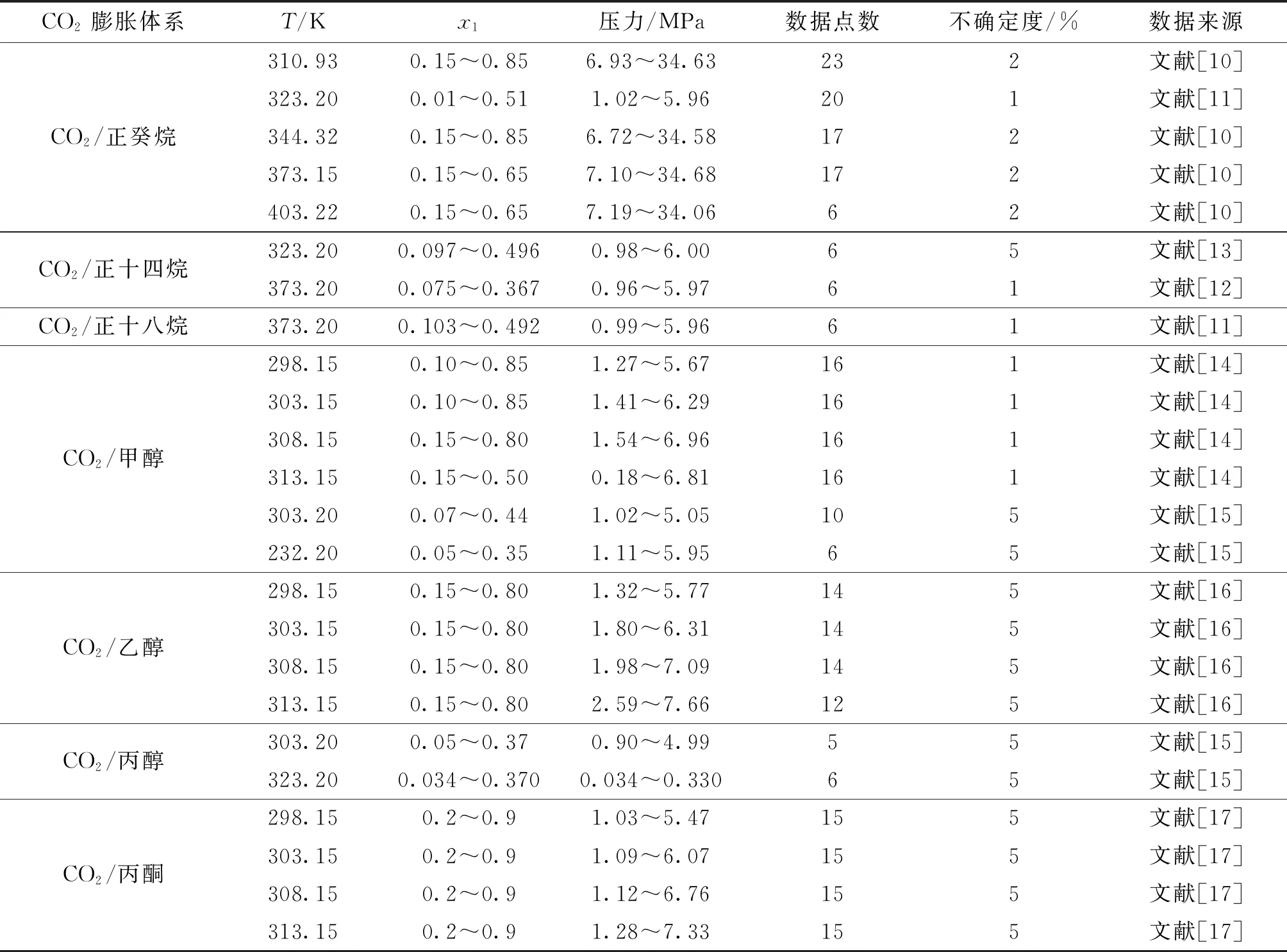
表1 CO2膨胀体系黏度的相关数据

为了比较,表3还给出了原始Eyring-NRTL黏度模型、McAllister三体模型、Setchenow方程以及Eyring-MTSM模型的计算值与文献值的绝对平均偏差。

从图3中可以看出:混合物中CO2的摩尔分数小于0.5时,本文计算值与文献值的偏差基本都在5%以内;当摩尔分数超过0.5以后,偏差呈现增大的趋势。从图1和图2可以看出,随着CO2摩尔分数的增大,混合物的黏度逐渐降低,这会造成计算偏差一定程度的增大。另一方面,仔细分析图3可以发现,计算偏差中较大的数据点主要为CO2/正癸烷、CO2/乙醇、CO2/丙醇体系的个别数据点。根据表3,其他模型的计算结果在这些数据点偏差也比较大,因此后续研究过程中应该更关注CO2摩尔分数较大时气液膨胀体系黏度的精确测试。

图3 CO2膨胀体系的黏度计算数据偏差分布

此外,从表3中还可以看出,除了CO2/丙酮体系,本文提出的黏度模型与Setchenow方程具有相似的计算精度,且均优于原始的Eyring-NRTL黏度模型、McAllister三体模型和Eyring-MTSM模型。然而,Setchenow方程属经验的多参数方程,缺乏物理意义。总体来看,本文改进的黏度模型具有一定的优势。

表2 拟合方程(6)中各系数的计算值

表3 黏度模型计算值与文献值的绝对平均偏差

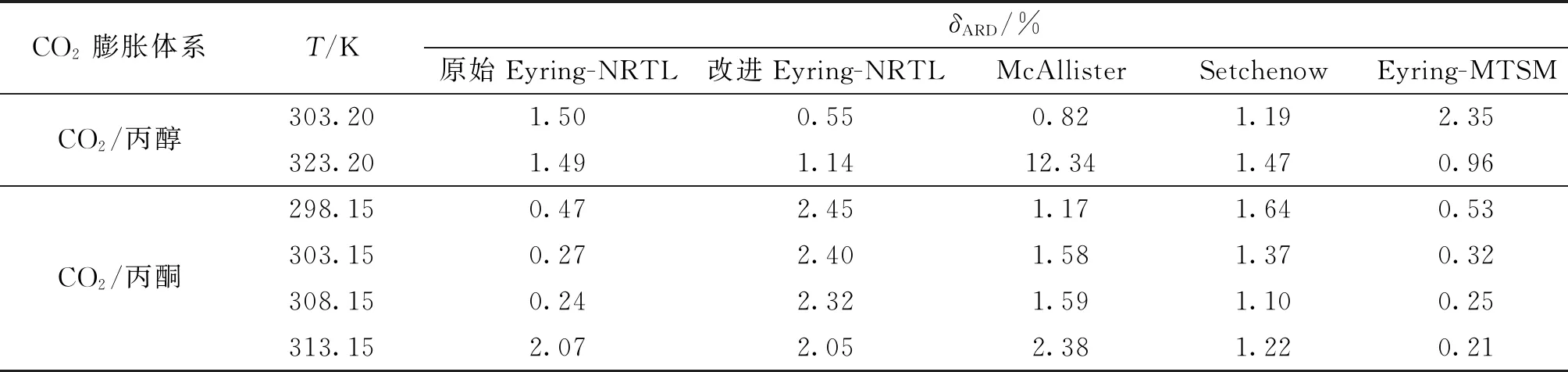
续表3

3 结 论

本文在对CO2膨胀体系的气液混合溶液黏度数据收集整理的基础上,对Eyring-NRTL二元混合物黏度模型进行了改进,建立了适用于CO2膨胀体系的气液混合物的黏度模型。将本文模型与其他3种模型进行了比较,结果表明本文提出的基于Eyring-NRTL的改进模型计算精度较高。在对应的温度下,本文模型黏度计算值的绝对平均偏差总体小于4%(CO2/正癸烷除外),说明其对CO2膨胀体系的气液混合溶液黏度关联计算是适用的。