未知系数的二阶线性同余发生器截位还原*
孙宏宇,朱宣勇,郑群雄,2
1.中国人民解放军战略支援部队信息工程大学,郑州450001
2.中国科学院信息工程研究所 信息安全国家重点实验室,北京100093
1 引言
随机数在密码学、统计采样、蒙特卡洛模拟、数值分析、博弈论、彩票系统、摇号系统中有广泛的应用.真正的随机数是使用物理现象产生的,比如掷硬币、骰子、转轮等等,它们的缺点是效率比较低,无法满足实际中短时间产生大量随机数的需要,因此,实际中一般采用伪随机数来代替真正的随机数使用.
线性同余发生器(LCG)是一类重要的伪随机序列生成器,一阶LCG 的工作模式为:选取模数m和乘数a,选取一个常数项c,给出初态x0,按照如下的递归关系生成序列

一阶LCG 的缺陷之一是其生成序列的周期太短,最大周期为m.为了提高LCG 生成序列的周期,提出如下n(n>1)阶LCG

对于LCG 在密码学中的应用,我们关注的是其生成序列的可预测性问题,即给出一段序列的片段,能否准确预测后面的序列.设(xi)i≥0为LCG 生成的序列,在xi的全部比特已知的情况下,对序列的可预测性问题研究成果有:对于一阶LCG,Plumstead[1]的结果表明,即使参数a,c,m全部未知,在给出初始的一段较短的序列的情况下,也能以较高的精度预测后面的序列.她的算法的第一步可以在已知2 + logm拍连续数据的情况下,在logm的多项式时间里还原参数a,c,算法的第二步可以在至多出现2 + logm次错误后还原模数m.对于一般的高阶LCG,Boyar[2]的结果表明,对一般的模型假定函数ϕj已知,全部的系数αj和模数m未知,则可以在至多出现关于logm,p和n的多项式次错误后成功预测序列.
Knuth[3]说明了用线性同余方法生成的序列,其高位比特的随机性要优于低位比特,因此,为了提高LCG 的抗预测能力,Knuth[4]提出了一种新的生成序列的方法,该方法输出每一个xi的高位部分比特yi,例如输出高位1/2 部分比特.目前对于截位输出的LCG 的可预测性问题研究成果主要有:对于一阶LCG,Knuth[4]考虑了在模数m=2k已知,参数a,c未知,只知道发生器生成序列高位部分比特yi(yi=⌊xi/2l⌋)的条件下,序列的可预测性问题,他给出了一个攻击方法,如果给出连续的2l拍yi,则可以在O(2l)步内还原参数a,c和种子x0,如果给出连续的N拍yi,则可以在O(k2l/N)2步内还原参数a,c和种子x0.Frieze 等[5]的结果表明,在模数m和乘数a已知的条件下,如果给出d拍截位序列yi,其中yi为xi的高位比特,则可以在logm+d的多项式时间内重构xi.他们的算法对一些特殊的乘数a是会失败的,但是这些特殊的乘数构成的集合基数比较小,为O(m−ε),其中参数0<ε<1,且ε的取值与观测到的数据量有关,可用的观测数据越多,算法越可靠.Boyar[6]给出了一个多项式时间的预测算法,该算法可以在全部参数a,c,m未知,t≤O(log logm)的低位比特不使用的情况下,在至多出现O(logm)次错误后成功预测序列.Stern 等[7,8]研究了在全部参数a,c,m未知条件下,基于截位序列的发生器参数还原问题,给出了高效的还原算法.Contini 等[9]对Stern 算法的第二步进行了改进,改进后的算法更加简单可靠,需要的数据量更少.给定一组基,有限域上序列的每个元素可以表示成这组基的线性组合,相应系数称为坐标.Gutierrez 等[10]研究了在隐藏一部分坐标的情况下,一阶LCG 生成序列的可预测性问题,给出了一个多项式时间的预测算法.对于一般的高阶LCG,杨建斌[11]研究了其在全部参数已知的条件下,如何由截位序列还原整体序列的问题.相关的研究被进一步扩展到非线性同余发生器,详见文献[12–14].值得一提的是,Frieze和Stern 的方法都充分利用格这一工具进行求解,而本文也将利用格进行问题的分析求解.
目前对基于截位输出的未知参数的LCG 的可预测性问题,研究成果主要针对一阶LCG,而对二阶和高阶LCG,其研究成果较少.本文主要研究二阶LCG 模型xi+2=axi+1+bximodm的可预测性问题,在模数m=2k已知,系数a,b未知,发生器生成序列的高位s比特截位序列已知时,我们给出还原系数a,b和初态x0,x1的方法.我们将对系数a,b的还原问题转化为整数剩余类环Z/mZ 上的二元非线性同余方程组的求解问题,通过求解同余方程组得到a,b的值,然后使用环上截位序列的还原方法来还原初态x0,x1.实验结果表明,当模数m=232,发生器生成的序列为Z/mZ 上的二阶本原序列时,可以由140 拍连续的高位6 比特截位序列来还原系数a,b和初态x0,x1,从而实现对序列的预测.另外,我们还进一步研究了带常数项c的模型:xi+2=axi+1+bxi+cmodm,虽然带c的模型相比于不带c的模型稍微复杂一点,但研究方法没有本质区别,我们将在文章第6节对带c的模型做简单的讨论.
论文的后续章节安排如下:第2节为预备知识,介绍后文需要用到的概念和引理; 第3节和第4节分别介绍如何还原系数a,b和初态x0,x1; 第5节给出整体还原的实验结果; 第6节讨论了带常数项c的模型的还原方法; 第7节总结了本文的工作,并提出值得进一步研究的问题.
2 预备知识
本节主要介绍整数剩余类环上序列的特征多项式与极小多项式、伴随矩阵的概念与性质、格的基本理论与格基约化算法.
2.1 整数剩余类环上序列的基本概念与性质
定义1设Z/mZ 表示模m的整数剩余类环,f(x)=xn−cn−1xn−1−···−c1x−c0modm是Z/mZ 上的n次首一多项式,若Z/mZ 上序列满足递归关系式


对j≥0,定义左移运算如下

在定义1中,如果f(0)是环Z/mZ 中的可逆元,即gcd(f(0),m)=1,则存在正整数T使得f(x)整除xT−1.最小的这样的正整数T称为f(x)的周期,并记为per(f(x),m),当m=pe时,有per(f(x),pe)≤pe−1(pn−1).
定义2设pe是素数方幂,f(x)是Z/peZ 上的n次首一多项式.若per(f(x),pe)=pe−1(pn−1),则称f(x)是Z/peZ 上的n次本原多项式.进一步,若序列且则称是Z/peZ 上的n阶本原序列.
当f(x)是Z/peZ 上的n次本原多项式时,对任意的i∈{1,··· ,e−1},f(x)modpi也是Z/piZ 上的n次本原多项式,即per(f(x),pi)=pi−1(pn−1).特别地,f(x)modp是素域Z/pZ 上的n次本原多项式.
2.2 伴随矩阵
定义3设A=(ai,j)1≤i,j≤n为n×n矩阵,A中元素ai,j的余子式Mi,j为A去掉第i行和第j列后剩下的(n−1)×(n−1)矩阵的行列式,ai,j的代数余子式Ai,j=(−1)i+jMi,j,则矩阵A∗=(Ai,j)1≤i,j≤n的转置称为A的伴随矩阵.
伴随矩阵满足如下性质,设d=det(A)为矩阵A的行列式,I为单位矩阵,则

因此,在Z/mZ 上A可逆当且仅当gcd(d,m)=1.假设A在Z/mZ 上可逆,令d−1为d在Z/mZ 上的逆元,令A−1为A在Z/mZ 上的逆矩阵,则

2.3 格的基本概念和性质
本文中的格全部以行向量为格基.
定义4设是Rn中的l个线性无关的向量,则n维欧几里得空间中以为基的l维格L定义为

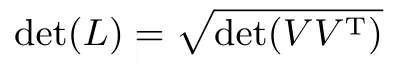
特别地,当l=n时,V是一个方阵,此时
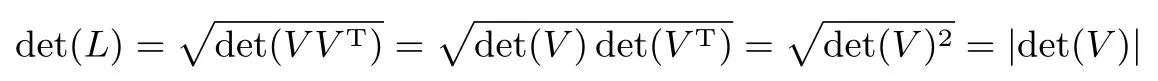
定义5(逐次最小长度)设L是一个格,以原点为球心,包含L中i个线性无关格向量的最小球的半径,称为L的第i个逐次最小长度,并记为λi.特别地,λ1是L的最短非零向量长度.
引理1[15]在一个n维随机格中,对所有的1≤i≤n,逐次最小长度λi以很大概率满足
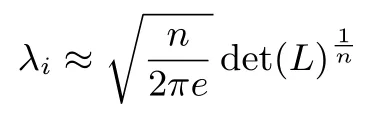
我们用∥∥来表示向量的欧几里得范数.格中主要关注如下两类困难问题
(1)最短向量问题(SVP):给定格L,找到一个非零向量使得对任意的非零向量有
(2)最近向量问题(CVP):给定格L和目标相量找到一个非零向量使得对任意的非零向量有
SVP和CVP 都是格领域研究的热点问题,已证明他们都是NP 难的.
2.4 格基约化算法
1982年A.K.Lenstra,H.W.Lenstra和L.Lovasz 提出了LLL 算法[16],LLL 算法是第一个也是最著名的近似求解SVP 问题的算法.Schnorr和Euchner 提出的BKZ 算法[17]是通过引入枚举算法来求取特定块内的最短向量,并多次调用LLL 算法进行约化,从而使得算法的实际求解效果更好.Chen和Nguyen 提出的BKZ 2.0[18]在实际求解中可以提高格基约化算法的效率.
输入格中的任意一组基,LLL 算法可以输出一组约化基,约化基满足如下性质.
引理2[16]设LLL 算法的约化参数为是LLL 算法输出的格L的一组约化基,λi是L的第i个逐次最小长度,则
注1实际中LLL 算法的约化参数通常设置为此时ρ=2.
3 还原系数a,b
本文我们研究二阶LCG 模型

的可预测性问题,条件为模数m=2k已知,系数a,b未知,给出发生器生成序列的高位s比特的截位序列.我们首先还原系数a,b,然后利用环上截位序列的还原方法还原初态x0,x1,实现对序列的预测.
我们假定k为模数m的比特位数,即k=logm,其中logm表示以2 为底m的对数,本文中出现的所有对数都以2 为底.二阶LCG 生成的序列为是xi的高位s比特值,zi是未知的低位部分比特值.令α=s/k,β=1−α,则可以写成

令

则由序列的递归关系式,对所有的i≥1,j≥0 有
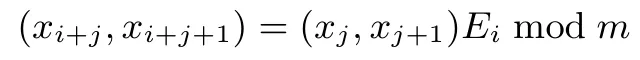
设Ei的第一个列向量为其中ei,0,ei,1都是关于a,b的整系数多项式,则有

下面我们首先将对a,b的还原问题转化为整数剩余类环Z/mZ 上的二元非线性同余方程组的求解问题,然后设计算法求解同余方程组得到a,b的值.
3.1 问题转化
Stern 等[7,8]在研究基于截位输出的一阶LCG 模型的参数还原问题时给出利用格工具来解决问题的方法,本节的问题转化过程是将Stern 的方法推广到二阶LCG 模型,首先我们给出一个必要的引理.
引理3[8]设是t维空间中的一组整数向量,t 其中max|ηi|≤B,且B满足 选取参数r,t,r>t>2,构造向量 其中i=0,1,··· ,r−1.由引理3知存在整系数η0,··· ,ηr−1,使得 其中|ηi|≤B,且B满足 引理3中虽然说明了η0,··· ,ηr−1的存在性,但并未说明如何求取η0,··· ,ηr−1的值,文献[8]给出了如下利用格基约化算法来求取η0,··· ,ηr−1的值的方法. 引理4[8]设K是一个常数且其中B如式(4)定义,构造格L 使用格基约化算法对L进行约化,则约化后的矩阵具有如下特征:存在某行(或某几行)的前t个坐标都是0.此时,η0,··· ,ηr−1就是这样的行向量(0,··· ,0,η0,··· ,ηr−1)的后面r个坐标. 注2η0,··· ,ηr−1的值不唯一,单次调用格基约化算法一般可以得到多组满足条件的η0,··· ,ηr−1的值. 引理4中的格L的维数为r,如果使用LLL 算法寻找系数,LLL 算法的约化参数设置为由引理2,考虑LLL 算法的求解误差,可得 令 结合式(1)和式(3)有 注意到|zi|<2βk,因此由Cauchy-Schwarz 不等式,有 结合式(4)和式(5)有 注3这里我们需要用到的是格L(e,m,t)中最短非零向量长度的下界,然而目前的格理论无法给出一个精确的下界,因此我们只能用引理1对最短非零向量的长度进行估计. 由于我们对格L(e,m,t)中最短非零向量的长度的估计并不精确,所以式(7)成立并无法保证一定成立.我们对长度上界的估计一般比的实际长度大很多,所以也有可能出现我们选取的参数不满足式(7)但却可以使成立的情况.下面类似于文献[8]的讨论,我们给出一个参数r,t的大概的选取标准.由式(6)可知,向量长度的上界可得 因为k=logm,可得对任意δ>0 有因此,只需要满足即可.实际中针对本文的二阶模型比较容易选取到参数r,t使得成立. 即 其中f(a,b)和g(a,b)都是关于a,b的整系数多项式且 如果式(8)只有零解,则我们可以得到 因此,我们可以通过求解同余方程组(9)得到a,b的值. 下面我们讨论式(8)只有零解的条件和概率.设 D为t×2 阶矩阵,令rank(Dmod 2)表示矩阵Dmod 2 的秩,下面的定理将给出式(8)只有零解的充要条件. 定理1设模数m=2k,则式(8)只有零解当且仅当rank(Dmod 2)=2. 证明:如果rank(Dmod 2)=2,设D0为D的一个2×2 的子矩阵且D0mod 2 为Dmod 2 的一个极大线性无关组,则有 即gcd(d,2)=1,因此,由2.2节可知D0在Z/2kZ 上是可逆的.考虑如下同余方程组 由此可知式(10)在Z/2kZ 上只有零解,进而式(8)在Z/2kZ 上只有零解. 如果在Z/2Z 上rank(D)<2,设Di,j为D的第i行和第j行形成的2×2 矩阵,其中0≤i,j≤t−1且i=j,则 综上,定理结论得证. 由定理1,我们将式(8)是否只有零解的问题转化为rank(Dmod 2)的值是否达到2 的问题.结合环上序列的性质,下引理5将给出rank(Dmod 2)的取值. 引理5设m(x)为序列在Z/2Z 上的极小多项式,则 证明:设rank(Dmod 2)=h,deg(m(x))=l.设矩阵D的前两个列向量分别为则由式(8)有 如果f(a,b),g(a,b)在Z/2Z 上只有0 解,则显然有h=l=2. 如果f(a,b),g(a,b)在Z/2Z 上存在非0 解,则有 如果g(a,b)=0 mod 2,f(a,b)=1 mod 2,显然有l=0 且此时Dmod 2 为全0 矩阵,故h=l=0. 如果g(a,b)=1 mod 2 且此时显然有h=l=1. 综上,引理结论成立. 结合定理1 与引理5,下面的定理2将给出式(8)只有零解的概率. 定理2设模数m=2k,如果随机选取系数a,b与初态x0,x1,则式(8)只有零解的概率 证明:令h(x)=x2−ax−b,且由引理5,rank(Dmod 2)的值即为序列在Z/2Z 上极小多项式的次数. 在Z/2Z 上h(x)mod 2 有以下四种可能的取值:h(x)=x2,h(x)=x2+1,h(x)=x2+x,h(x)=x2+x+1.在系数a,b随机选取的条件下,h(x)取到上面每种可能取值的概率都为 如果h(x)=x2,即a=0 mod 2,b=0 mod 2,则G(h(x),2)的全部四条序列为(0,0,0,0,···),(0,1,0,0,···),(1,0,0,0,···),(1,1,0,0,···),其中有两条序列(0,1,0,0,···)和(1,1,0,0,···)以h(x)为极小多项式,故以h(x)为极小多项式的序列出现的概率为 如果h(x)=x2+1,即a=0 mod 2,b=1 mod 2,则G(h(x),2)的全部四条序列中有两条序列(0,1,0,1,···)和(1,0,1,0,···)以h(x)为极小多项式,故以h(x)为极小多项式的序列出现的概率为 如果h(x)=x2+x,即a=1 mod 2,b=0 mod 2,则G(h(x),2)的全部四条序列中只有一条序列(0,1,1,1,···)以h(x)为极小多项式,故以h(x)为极小多项式的序列出现的概率为 如果h(x)=x2+x+1,即a=1 mod 2,b=1 mod 2,则h(x)为不可约多项式,G(h(x),2)的全部四条序列中除了全零序列(0,0,0,0,···)外都以h(x)为极小多项式,故以h(x)为极小多项式的序列出现的概率为 注4由定理2可知,在随机选取系数a,b与初态x0,x1的条件下,式(8)只有零解的概率为如果随机选取系数a,b与初态x0,x1往往会得到一些伪随机性质较差的序列,例如得到的序列周期很短,因此,考虑到实际应用,后文在进行实验时只考虑Z/2kZ 上的本原序列.由2.1节可知,如果h(x)是Z/2kZ 上的本原多项式,h(x)mod 2 也是Z/2Z 上的本原多项式,则一定有rank(Dmod 2)=2,故可以保证式(8)只有零解,即确保式(9)一定成立. 由3.1节的讨论可知,我们将对a,b的还原问题转化为对同余方程组(9)的求解问题.式(9)中的f(a,b)和g(a,b)都是关于a,b的次数小于等于r−2 的二元多项式.所以对式(9)的求解相当于在整数剩余类环Z/mZ 上求解一个含有两个未知变元的非线性同余方程组,其中每个非线性同余方程关于未知变元的次数都小于等于r−2. 在实际求解中选取的参数r的值一般在50 左右,即非线性同余方程的次数一般在50 次左右,当模数m较大时(例如m=232或m=264),用数学软件maple 中的同余方程求解命令无法求出结果,因此,我们给出了一个基于比特分位的分层求解算法: 设模数m=2k, 是Z/mZ 上关于变量u,v的二元非线性多项式,其中ci,j∈Z/mZ 是多项式的系数,设u=[u0,··· ,uk−1]与v=[v0,··· ,vk−1]分别为u,v的比特分位表示方式,即u,v的二进制比特分位展开式分别为 则 求解f(u,v)=0 modm等价于求解u,v的每个比特ui,vi,0≤i≤k−1 的值,我们按照由低位到高位逐比特求解ui,vi的值.首先令模数m=2,求解 得到u0,v0的值.然后令模数m=22,将u0,v0的值代入f(u,v)中求解 得到u1,v1的值,···,这样依次求解,直到令模数m=2k,将u0,v0,··· ,uk−2,vk−2的值代入f(u,v)中求解 得到uk−1,vk−1的值为止. 对于1≤q≤k−1,求解uq,vq的方程为 所以有 因此,求解uq,vq的值等价于在Z/2Z 上求解如下的比特方程 如上所述,求解f(u,v)=0 modm等价于在Z/2Z 上依次求解如下k个比特方程 我们给出如下定理. 定理3设f(u,v)=0 modm是关于变量u,v的二元非线性同余方程,模数m=2k.设u=[u0,··· ,uk−1]与v=[v0,··· ,vk−1]分别为u,v的比特分位表示方式,按照上述方法由低位到高位逐比特求解uq,vq的值,则有以下两个结论成立. (1)对每一个1≤q≤k−1,fq(u0,v0,··· ,uq,vq)都是Z/2Z 上关于uq,vq的线性方程. (2)对每一个1≤q≤k−1,求解fq(u0,v0,··· ,uq,vq)=0 mod 2 得到的uq,vq的解的个数都相同,且uq,vq的解的个数只取决于u0,v0的值. 证明:由式(12)可知,对每一个1≤q≤k−1,fq(u0,v0,··· ,uq,vq)中不存在关于uq,vq的非线性项,故fq(u0,v0,··· ,uq,vq)是线性的,即结论(1)成立. 进一步,由式(12)我们可以发现uq,vq的系数只与ci,j,i,j,u0,v0的值有关,当方程 给定以后,ci,j,i,j的值便确定,则uq,vq的系数只取决于u0,v0的值,因此,对每一个1≤q≤k−1,求解fq(u0,v0,··· ,uq,vq)=0 mod 2 得到的uq,vq的解的个数都相同,且uq,vq的解的个数只取决于u0,v0的值,即结论(2)成立. 综上,定理的结论成立. 设a=[a0,··· ,ak−1]与b=[b0,··· ,bk−1]分别为a,b的比特分位表示方式,首先我们求解 得到a0,b0的值,易知a0,b0有不超过4 组取值.从a0,b0的任意一组取值出发逐层向上求解ai,bi,i=1,··· ,k−1,由定理3可知求解ai,bi相当于在Z/2Z 上求解一个线性方程组. 不妨设在求解ai,bi,1≤i≤k−1时的线性方程组为 其中d1,d2,d3,d4,w1,w2为常数,对于给定的引理4中格基约化算法输出的η0,··· ,ηr−1,这些常数的值由a0,··· ,ai−1,b0,··· ,bi−1的值唯一确定.在Z/2Z 上,设上面方程组的系数矩阵 的秩为rank1,设增广矩阵 的秩为rank2,则由线性方程组的求解理论可知: 如果rank1 < rank2,则ai,bi无解,说明前面求出的a0,··· ,ai−1,b0,··· ,bi−1的值是错误的,可以舍弃; 如果rank1=rank2=2,则ai,bi只有一组解; 如果rank1=rank2=1,则ai,bi有两组解; 如果rank1=rank2=0,则ai,bi有四组解. 由上面的讨论可知,当1≤i≤k−1时,ai,bi可能存在一组解,两组解或四组解这三种情况,如果存在较多的i的取值使得ai,bi的解的个数多于一组,则会导致解的数量迅速膨胀,求解的时间和存储空间开销也会急剧增加,造成实际求解困难.在注2 中我们提到单次求解一般可以得到多组满足条件的η0,··· ,ηr−1的值,因此也可以得到多个同余方程组(9),我们可以通过同时求解多个同余方程组来解决这一问题. 设模数m=2k,同时求解n个同余方程组,从a0,b0某一组取值出发,在求解a1,b1时可以写为 设上面等式的系数矩阵为D,如果rank(Dmod 2)=2,则a1,b1有唯一解.下面我们假设d1,··· ,d4n在mod 2 后都是0,1 随机的,则在Dmod 2 的全部24n种可能取值中,使得rank(Dmod 2)=0 的取值只有全零1 种.使得rank(Dmod 2)=1 的取值为矩阵Dmod 2 的2n行中有j(1≤j≤2n)行为(0,1)(或(1,0),(1,1)),其余2n−j行全为(0,0),故有种情况.因此,a1,b1有唯一解的概率为 由定理3的结论(2)可知,如果a1,b1有唯一解,则每一层的ai,bi,1≤i≤k−1 都有唯一解,因此从第2层到最高层每一层都有唯一解的概率为P.对于n的不同取值对应的P的值如表1 所示. 表1 n 与P 的对应取值Table 1 Corresponding values of n and P 针对上面的讨论,我们设计了如下实验进行验证.固定模数m=232,在Z/mZ 上随机选取100 个本原多项式h(x)=x2−ax−b,每个本原多项式随机生成一条Z/mZ 上的二阶本原序列,截取高位s=6 比特作为输出序列,取参数r=115,t=25,一次同时求解n个同余方程组,我们分别测试了n=1,2,3,4,5,6时这100 组数据中满足从第2 层到最高层每一层的ai,bi,1≤i≤31 都有唯一解所占的比例,结果如表2 所示. 表2 实验测得的比例Table 2 Experimentally tested ratio 注5将表1 与表2 进行对比可以发现实验数据与理论结果比较吻合,无论是基于理论结果还是实验数据,我们都可以认为如果我们一次同时求解5 个同余方程组,有90% 的同余方程组可以保证从第2 层到最高层每一层都有唯一解,这样的同余方程组是很容易求解的.当然这并不意味着剩下的10% 一定是难以求解的,在剩余的10% 中除个别情况外,大部分也是容易求解的,实际上只要使ai,bi的解的个数不唯一的i的取值不是太多,同余方程组都是容易求解的. 按照上面的方法由低位比特向高位比特逐比特求解ai,bi的值,最终可以得到a,b的值.这里需要指出的是,可能存在多组使式(9)成立的a,b的值,我们的算法会将它们全部找出来,究竟哪一组a,b的值是我们需要的,这一问题需要我们结合后面的还原结果做进一步判断. 这一节我们将结合第3节还原出的a,b的值,使用环上截位序列的还原方法还原初态x0,x1. 杨建斌[11]研究了已知参数条件下的整数剩余类环上截位序列的还原问题,他在文章中研究的具体问题为:设模数m是奇数,f(x)是Z/mZ 上的本原多项式,已知f(x)生成序列的低位l比特的截位序列,要求还原序列的初态.他使用的方法是将截位序列的还原问题转化为线性同余方程组中小整数解的求解问题,然后利用Frieze 等人[5]给出的线性同余方程组小整数解的求解方法进行求解.实际上他的方法对于f(x)是非本原多项式的情况以及模数m是偶数,已知的截位序列是高位比特的情况同样是适用的.在第3节还原出a,b的值后,对初态x0,x1的还原问题即相当于在已知参数条件下环上截位序列的还原问题,可以直接使用杨建斌的方法实现对初态x0,x1的还原. 我们用d表示使用的截位序列的总拍数,即d=r+t,令式(2)中的2≤i≤d−1,j=0,将式(1)代入式(2)得到 写成矩阵形式为 其中pi=2βk(yi−ei,0y0−ei,1y1),2≤i≤d−1. 构造如下的格L(e,m,d) 格L(e,m,d)是d维格,使用格基约化算法约化格L(e,m,d),得到约化基W=(wi,j)0≤i,j≤d−1.令向量由杨建斌[11]的结论可知,如果对所有的0≤i≤d−1 都有 则可以还原初态x0,x1. 由注4 的讨论,在进行还原效果验证时我们只考虑Z/mZ 上的本原序列.固定模数m=232,在Z/mZ 上随机选取100 个本原多项式h(x)=x2−ax−b,每个本原多项式随机生成一条Z/mZ 上的二阶本原序列,截取高位s=6 比特作为输出序列,取参数r=115,t=25,即使用d=r+t=140 拍截位序列,一次同时求解n个同余方程组,我们分别测试了n=1,2,3,4,5时对应的求解成功率如表3所示,这里的成功率指的是在100 组数据中,可以由截位序列成功还原出系数a,b和初态x0,x1所占的比例. 注6实验中我们同时求解n(n=1,2,3,4,5)个同余方程组,这n个同余方程组是使用引理4中格基约化算法输出的前n个行向量作为η0,··· ,ηr−1得到的.在表3中,当n=5时有两组求解失败,原因可能是使用的η0,··· ,ηr−1存在不能使成立的情况.另外,在求解同余方程组时,出于实验效率的考虑,我们只求解从第2 层到最高层每一层都有唯一解这种情况,因此有可能丢掉正确的解,这也是出现两组求解失败的可能原因. 表3 整体还原效果Table 3 Total reconstruction effect 注7本文的所有实验都基于NTL[19]库中的代码实现,使用的格基约化算法为BKZ 算法(分块数设置为20,约化参数设置为0.99). 我们进一步研究了xi+2=axi+1+bxi+cmodm这种带c模型的截位还原问题,针对这种模型,我们将构造的向量调整为 则可以使用与本文第3 节相同的方法还原系数a,b.关于对常数项c和初态x0,x1的还原问题,我们使用的方法是将常数项c看作是系数为1 的初态,使用本文第4节的方法将常数项c与初态x0,x1同时进行还原.我们现在还无法做到在常数项c完全未知的情况下实现还原,这里我们需要已知常数项c的高位s比特. 就还原效果而言,主要受还原常数项c和初态x0,x1这一步的限制,当模数m=232时,我们的截位比特数s最小只能取到20,还原效果相比于不带c的模型要差很多,我们还没有找到形成这种差异的原因. 本文研究了在模数m=2k已知,系数a,b未知的条件下二阶LCG 模型的截位还原问题,实现对二阶LCG 生成序列的预测.本文的方法对于模数m为素数方幂,即m=pe时同样有效,这种情况在求解同余方程组时需要将a,b进行p-adic 展开,每一个分位在Z/pZ 上求解.理论上本文的方法可以向一般的高阶模型推广,推广过程中可以预见到的主要难点之一是对含有多个变元的高次非线性同余方程组的求解.另外,在模数m是一般的合数或m未知的条件下如何还原也是值得进一步研究的问题.

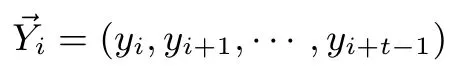









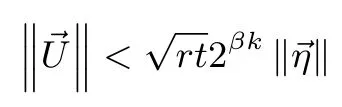
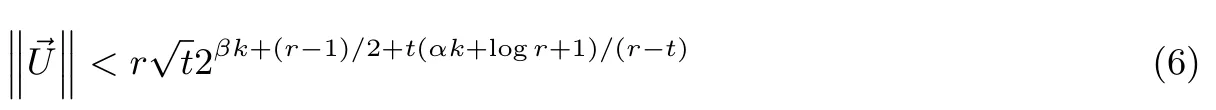
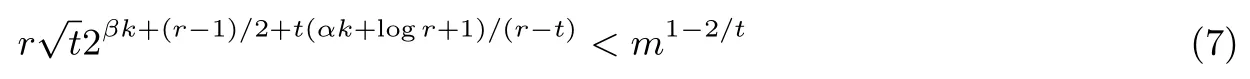





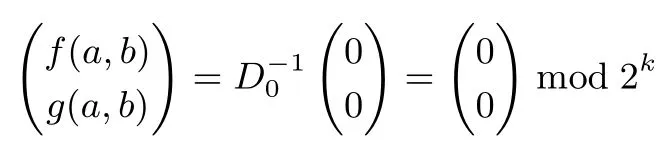
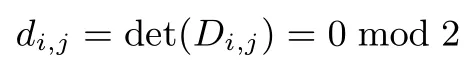



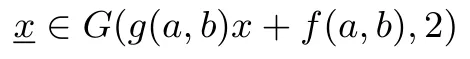
3.2 求取a,b 的值



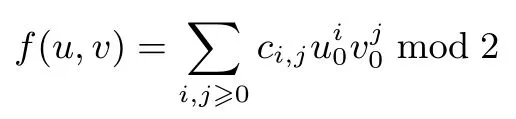







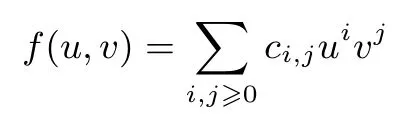








4 还原初态x0,x1




5 整体还原效果

6 带c模型的讨论

7 结束语

