超音速分离线喷管内流场数值模拟①

李 鑫，李 耿，王周成，张 飞，赵 康，刘元敏

(中国航天科技集团有限公司四院四十一所，西安 710025)

0 引言

超音速分离线喷管(Supersonic Splitline Nozzle)是固定部分与可动部分之间的分界线位于喷管超音速区域的一种矢量喷管[1]。相比亚音速分离线喷管，具有零部件数量少、结构简单、偏转效率高以及能够减小发动机后开口尺寸等一系列优点，欧美等发达国家在这一领域开展了较系统的研究，并在多发战术发动机和大型发动机上进行了热试车[2-6]。

本文通过流场仿真，给出了超音速分离线喷管不同摆角下的内流场分布规律，获得了喷管的受力情况，对比分析了超音速分离线与亚音速分离线喷管的偏转效率，并给出了摆动对喷管内两相流粒子浓度分布的影响，为喷管设计及工程研制提供理论参考。

1 数学与物理模型

图1给出了超音速分离线与亚音速分离线喷管(Subsonic Splitline Nozzle)的摆动对比示意图。可看出，亚音速分离线喷管在摆动过程中喷管内型面保持不变，内流场基本不受干扰；而超音速分离线喷管的摆动使得内型面发生了较明显的变化，内流场出现了复杂的压缩-膨胀波系[7]，流场不再具备轴对称的特点，从而可能会对喷管的气动力及烧蚀情况造成影响。

1.1 基本假设

固体火箭发动机内流场的流动属于典型的二相流动过程，这里采用Euler-Lagrangian法对该过程进行数值模拟。在Euler坐标系中求解气相控制方程，同时在Lagrangian坐标系中对凝相颗粒进行跟踪，两者之间的耦合通过在控制方程增加源项来完成。

在进行数值计算时，对内流场的流动做如下假设：

(1)不考虑燃气中的化学反应；

(2)不考虑凝相的燃烧、蒸发、破碎过程；

(3)假设过程为定常流动。

(a)亚音速分离线喷管

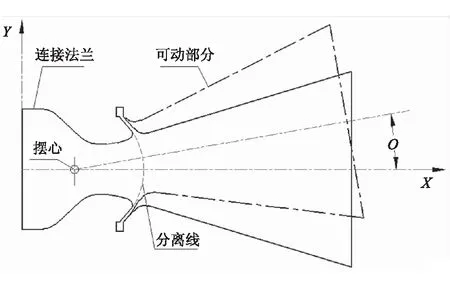
(b)超音速分离线喷管

1.2 气相控制方程

气相质量守恒方程：

(1)

气相动量守恒方程：

(2)

考虑凝相的作用，气相的能量守恒方程为

(3)

式中I为比内能；Qd为颗粒作用的能量源相；σ为热通量项，包括热传导项和焓扩散项。

1.3 两相流模型

两相流模型采用DDM(Discret Droplet Model )模型，将颗粒看成离散质点，颗粒的运动方程为

(4)

颗粒的轨迹方程为

(5)

颗粒的能量方程为

(6)

式中hp为颗粒表面对流换热系数；Ap为颗粒表面积。

在Lagrangian坐标系下，对每个粒子进行跟踪，计算颗粒相的质量、动量、能量与连续相的交换量成为源相，加入到随后连续相的计算中，连续相计算又对凝相计算产生影响，二者交替计算，直至收敛[8-13]。

1.4 物理模型及计算域

采用ICEM软件进行六面体网格划分，为保证计算结果准确，对壁面处网格进行加密处理，确保第一个内节点P位于对数分布律成立的范围内。采用疏密两种网格进行网格无关性验证，以发动机推力作为指标。0°摆角结果表明，两种网格计算得到的发动机轴向推力几乎完全一致，侧向推力相差0.075%。因此，较稀疏的网格完全可满足计算要求。

图2为超音速分离线喷管计算模型及网格划分情况。喷管喉径为φ81 mm，入口部位收敛比为5.7，出口扩张比为15.2，活动体与固定体分界线位于喉部下游，扩张比为1.7，处于超音速流场区域。扩张段型面为直锥型。为了提高精度和计算效率，采用结构网格离散计算区域[14-15]，网格数量为66.16万。

(a)对称面网格

(b)表面网格

2 物性参数及边界条件

数值计算采用FLUENT 软件。燃气的定压比热容和气体常数根据热力计算结果获得，燃气密度按照理想气体状态方程给定，粘性系数按照Sutherland公式计算，热导率选择kinetic-theory。因标准κ-ε湍流模型用于强旋流或者带有弯曲的壁面流动时会出现一定失真，这里选用RNGκ-ε模型提高数值计算的准确度。气相压力入口边界为入口压强10 MPa，总温3781 K。气相压力出口边界为出口压强101 325 Pa，出口环境温度293 K。气相壁面边界条件采用无滑移及绝热壁面边界条件；假定凝相粒子的直径遵循Rosin-Rammler分布，平均粒径为4×10-5m，粒径范围为1×10-5～4×10-5m，凝相粒子的初始速度为0.1 m/s，压力入口及出口均采用逃逸边界，壁面采用反弹模型[16]。

3 计算结果与分析

相比亚音速喷管，超音速分离线喷管的摆动会对喷管内流场分布及喷管的气动力产生更大的影响。因此，本文以喷管摆角作为主要变量，对0°、2.5°、5.0°、7.5°、10.0°不同摆角下的内流场进行计算分析。

3.1 不同摆角对马赫数分布云图的影响

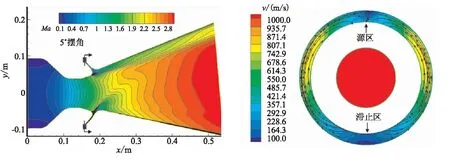
图3～图5给出了超音速分离线喷管0°、5.0°、10.0°三个典型摆角下摆动平面内内流场马赫数分布云图及分离线位置狭缝区域环向剖面的速度和流线分布图。从图3可看出，0°摆角下喷管内流场呈轴对称分布，喷管入口燃气经过收敛段加速之后在喉部达到音速，之后经扩张段进一步加速为超音速气流；燃气在喷管活动体小端部位产生了一系列锥形压缩波，此族压缩波没有在轴线附近封闭，在轴线附近还有一系列膨胀波，引导超音速气流继续加速直到喷管出口。0°摆角下分离线狭缝区域流速很低，最高速度仅为23.2 m/s，且区域内为不规则的漩涡流动。

(a)马赫数分布云图 (b)速度流线图

图4为5.0°摆角下喷管摆动平面内的马赫数云图及分离线狭缝区域环向剖面速度云图和流线图。从马赫数分布图可看出，相比0°摆角，超音速气流在喷管活动体小端的压缩波已增强为斜激波，而且喷管内流场已不再具有轴对称的特性。在喷管摆动平面内，活动体小端靠近轴线一侧的激波强度最强，而远离轴线一侧的激波强度则较弱。

从环向剖面的速度和流线图可看出，5.0°摆角下狭缝区域已经存在明显的由“滞止区”向“源区”的环向流动，部分区域的速度已经达到834.0 m/s。从马赫数云图可注意到，在“源区”与喷管扩张段相交的地方有一簇不规则曲面激波。这是因为“源区”附近狭缝区域的超音速气流必须经过激波的压缩以满足边界条件，然后再经过扩张段的扩张作用，加速达到超音速。

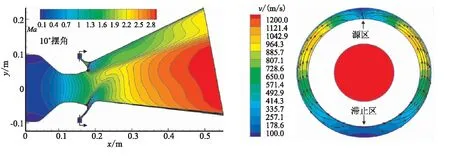
图5为10.0°摆角下喷管摆动平面内的马赫数云图及分离线狭缝区域环向剖面速度和流线图。从马赫数分布云图可看出，随着摆角的增大，喷管活动体小端产生的激波均进一步增强。其中，靠近轴线一侧活动体激波强度的增幅最大。

从环向剖面的速度和流线图可看出，10.0°摆角下狭缝区域的环向流动进一步加强，部分区域的速度已经达到1031.9 m/s。从马赫数云图可注意到，在“源区”与喷管扩张段相交地方的曲面激波也进一步增强。

(a)马赫数分布云图 (b)速度流线图

(a)马赫数分布云图 (b)速度流线图

3.2 不同摆角对压力分布云图的影响

图6～图8给出了超音速分离线喷管0°、5.0°和10.0°三个典型摆角下摆动平面内压力云图及分离线狭缝区域环向剖面的压力云图和流线分布图。从图6可看出，0°摆角下喷管内压力呈轴对称分布，由于活动体小端区域压缩波的存在，致使波后压强有小幅的增加。从分离线狭缝区的局部放大图可看出，0°摆角下区域内存在不规则漩涡流动。

从环向压力和流线图可看出，此时狭缝区内压强几乎处处相等，约为1.78 MPa，为流动滞止区，这与图3中速度分布趋势也相吻合。燃气在此区域速度很低，呈现不规则流动状态。

从图7可看出， 5.0°摆角下喷管内的压力分布已不具有轴对称的特征。由于活动体小端激波的存在，该区域压强进一步升高。在喷管摆动平面内，靠近轴线一侧的活动体小端的压强升高更加明显，远离轴线一侧的升高幅度则较小一些。另外，从分离线区域的局部放大图可看出，5.0°摆角下狭缝区域内的漩涡流动消失，转变为“源区”，源区内的压强较0°摆角下显著增大，达到2.81 MPa。

从环向剖面的压强和流线图可看出，5.0°摆角下分离线狭缝区域已经存在明显的环向压强差，“滞止区”即靠近喷管轴线的一侧压强最高，达到3.17 MPa，而远离轴线一侧的“源区”压强则较低，从而导致区域内形成了由“滞止区”向“源区”的环向流动。

从图8可看出，随着摆角的增大，喷管内压力场的非对称性进一步加强，活动体小端的压强也进一步增大。其中，靠近轴线一侧的压强增幅最大。从分离线区域的局部放大图可看出，10.0°摆角下狭缝区域内流动状态仍为“源区”，压强达到4.73 MPa。

从环向剖面的压强和流线图可看出，10.0°摆角下分离线狭缝区域环向压差进一步加大，“滞止区”即靠近喷管轴线的一侧压强最高，达到5.48 MPa，比“源区”高出2.76 MPa，这也致使区域内由“滞止区”向“源区”的环向流动进一步增强，流动速度增大。

(a)压力分布云图 (b)环向流线图

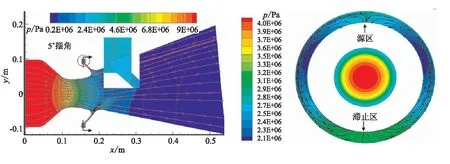
(a)压力分布云图 (b)环向流线图

(a)压力分布云图 (b)环向流线图

3.3 喷管受力及放大因子分析

从上述分析可知，摆动会引起超音速分离线喷管内流场的显著变化，从而导致喷管内的气动力分布改变，影响发动机的推力大小及方向。这里对不同摆角下超音速分离线喷管内流场进行压力积分，获得不同方向的受力情况，如表1所示。表1中，同时给出了亚音速分离线喷管对应摆角的受力情况。从表1可看出，在摆动角度相同的条件下，超音速分离线喷管的轴向力(X向)略小于亚音速分离线喷管，而径向力(Y向)则显著大于亚音速分离线喷管。这说明在摆动条件下，相比亚音速分离线喷管，超音速分离线喷管的轴向力略有损失，而径向力则有较明显的增大，即喷管的偏转效率会显著提高。从流场计算结果分析可知，造成上述现象的主要原因是超音速分离线喷管在摆动后引起了扩张段上非对称的压缩-膨胀波系，该波系导致气流进一步向着喷管的摆动方向发生了偏转，引起了径向力的增大，而在轴向上的分力则会相应减小。另外，超音速分离线喷管摆动引起的压缩-膨胀波系造成的流动损失，也是导致喷管轴向推力减小的原因。

由于径向力对飞行器的偏转起着主要作用，为便于研究，定义相同机械摆角下超音速分离线喷管和亚音速分离线喷管的径向力比值为喷管的偏转放大因子。图9和10分别给出了超音速分离线喷管轴向推力比值及偏转放大因子与摆角的关系。可知，随着摆角增大，超音速分离线喷管轴向力损失增大；而偏转放大因子则随着摆角增大呈现先增大、后减小的变化规律，但其值始终大于1.0，从本文算例来看，2.5°摆角时偏转放大达到最大，其值为1.36。

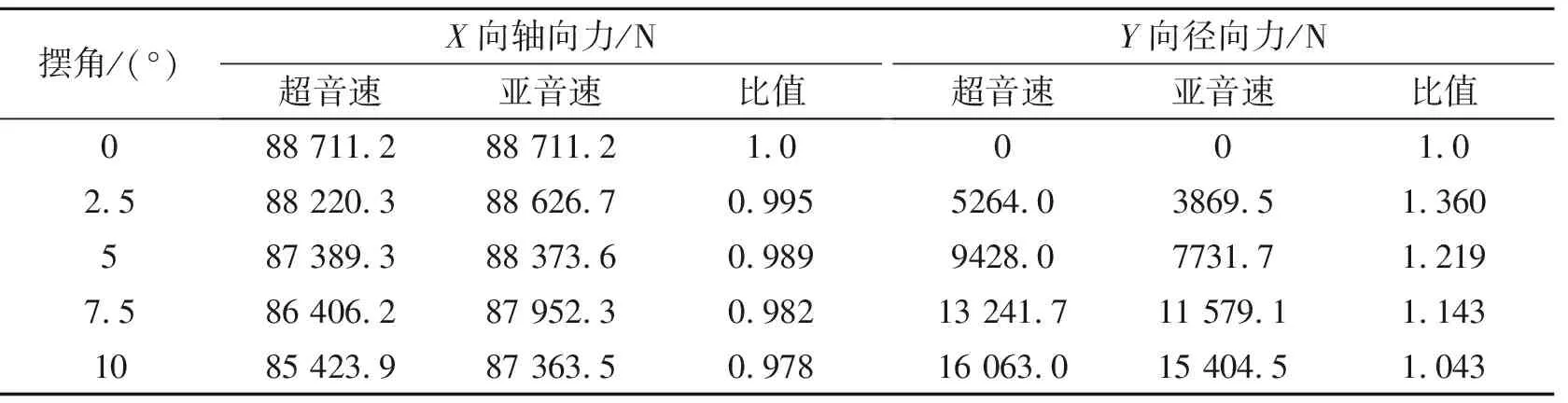
表1 喷管作用力随摆角变化情况对比

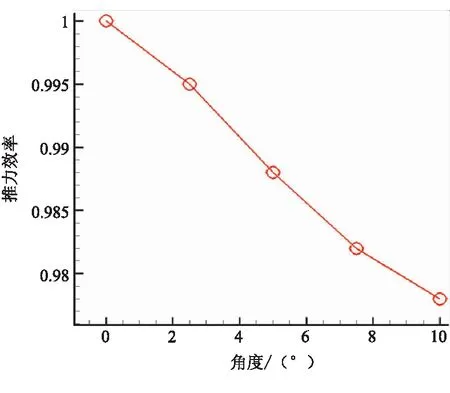
图9 轴向推力效率

图10 偏转放大因子

3.4 喷管偏转对粒子分布规律的影响

图11～图13给出了0°、5.0°、10.0°三个典型摆角下超音速分离线喷管内流场粒子浓度的分布情况。可看出，0°摆角下，Al2O3粒子基本集中在轴线附近，呈现对称分布，整个喷管喉部下游内壁面基本没有粒子的撞击，极限流线与壁面之间形成“无粒子区”[17]。5.0°摆角下，喷管活动体小端一侧由于摆动靠近流场的粒子集中区，在气相流场的共同作用下，Al2O3粒子的分布不再具有轴对称特性，靠近轴线一侧的活动体小端粒子浓度显著增大。当摆角达到10.0°时， Al2O3粒子分布的非对称特性进一步加剧，喷管活动体小端靠近轴线一侧受到粒子撞击，致使该区域粒子浓度进一步增加。

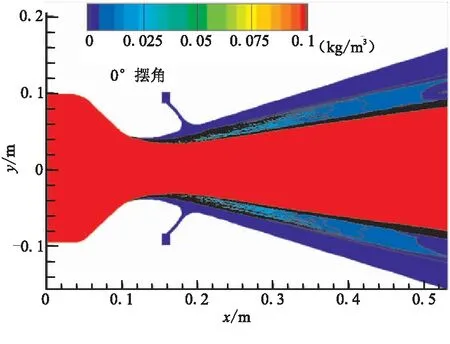
图11 粒子浓度分布(0°)

图12 粒子浓度分布(5.0°)

图13 粒子浓度分布(10.0°)

4 结论

(1)从计算结果可知，与亚音速分离线喷管不同，摆动条件下超音速分离线喷管内流场呈现显著的三维流动特征，且随着摆角增大，喷管内激波强度和内流场的非对称性不断增加。

(2)在相同摆角下，相比亚音速分离线喷管，超音速分离线喷管的轴向分力略有减小，而径向分力则呈现增大的趋势；超音速分离线喷管与亚音速分离线喷管的径向分力比值，即偏转放大因子，则随喷管摆角呈现先增大、后减小的变化规律，但其值始终大于1.0，本算例中的最佳放大因子为1.36，对应的喷管摆角为2.5°。

(3)随着摆角增大，超音速分离线喷管内流场Al2O3粒子分布的非对称性逐渐加强，喷管活动体小端的粒子浓度也逐渐增大，由此可能造成的烧蚀增大在超音速分离线喷管的热防护设计中应予以考虑。