波形切换对雷达距离测量的影响
庄 俊,杨 沛,王 鹏
(中国洛阳电子装备试验中心,河南 洛阳 471003)
0 引 言
雷达主要负责完成目标的探测、跟踪和识别,广泛应用于机载预警、导航、导弹制导、战场监视、靶场测量和气象探测等方面,是重要的军事装备[1]。
跟踪雷达为满足作用距离的需要,在不同的跟踪距离区间采用不同的波形参数,但在实际测试中发现:波形切换时会产生距离测量值的跳变,影响目标的稳定跟踪。本文对雷达波形切换时产生距离跳变的原因及其对雷达测距的影响进行了分析,并提出了针对性的解决方法,提高了雷达的目标跟踪稳定性。
1 雷达距离跟踪系统
1.1 雷达距离测量原理
现代雷达多使用脉冲压缩体制[2],脉冲压缩处理一般发射时使用长脉冲,接收时采用匹配滤波器进行频率调制,其实质是进行频率延时处理。脉冲压缩处理多通过数字方法来实现,数字方法又可分为时域脉冲压缩和频域脉冲压缩[3-4]。典型的频域脉冲压缩过程如图1所示。

图1 频域脉冲压缩原理框图
假设输入线性调频回波信号为s(t),匹配滤波器的频率响应为H(ω)[5],则:
(1)
H(ω)=Ks*(ϖ)exp(-j2πf0t)
(2)
式中:A为信号幅度;τ为脉冲宽度;f0为信号中心频率;k为调频斜率;rect(t/τ)为矩形函数;K为滤波器的增益常数。
不考虑多普勒频移(即fd=0)时,匹配滤波器的输出为:
cos2πf0(t-t0)
(3)
式中:D为脉冲压缩比,且有D=Bτ;t0为匹配滤波器输出固定时延。
线性调频信号经过匹配滤波后,输出包络为sinc函数,包络最大值在t=t0时刻[6]。雷达对目标距离的测量值是基于匹配滤波器的输出峰值出现的时间位置来确定的[7]。
1.2 雷达距离跟踪
雷达对目标距离跟踪的一般流程为:搜索发现目标后,首先根据目标的历史航迹预测目标的当前位置,并对目标回波信号采样(采样仅在以目标预测距离为中心的距离波门内进行)。信号处理系统对采样信号进行处理,根据和路信号回波的距离中心,得到目标距离偏离预测值的距离误差,并将目标的距离误差送上位机。上位机根据目标的预测位置坐标和测量得到的误差,滤波计算出测量时刻目标的距离和速度,并得到下一时刻目标位置预测值。重复上述预测和测量过程,完成对目标的持续跟踪。
2 波形切换对测距的影响
雷达为兼顾最小作用距离和最大作用距离的需要,在不同的跟踪距离区间采用不同的波形参数。某型雷达在各跟踪距离段采用的典型工作波形如表1所示。

表1 雷达各距离段工作波形
测试过程中,设置合作目标由远及近飞行,速度分别为200 m/s、1 000 m/s及2 000 m/s。记录雷达对目标的距离跟踪数据如图2所示。

图2 不同速度时目标距离测量曲线
由图2可见,当目标距离为9 km(即雷达波形切换时刻)时,雷达所测量的目标距离产生跳变,且不同速度目标回波引起的跳变距离不同。显然,目标速度与切换波形时的距离跳变现象存在关联。
3条测量曲线之间存在较为固定的距离差,说明距离测量存在误差,且该误差与目标速度之间存在一定关系。
多普勒频移是雷达测量目标相对速度的依据。对于利用多普勒频移进行测速的雷达,目标不同速度引起的多普勒频移不同[8]。多普勒频移会导致接收到的线性调频信号在频率上出现偏移,从而引起距离测量误差,称为距离-多普勒耦合效应[9-10]。下面进行详细分析。
当存在多普勒频移时,线性调频信号经过匹配滤波器的输出信号为:
cos2πf0(t-t0)
(4)
此时,匹配滤波器的输出信号包络峰值不在t=t0时刻,其输出峰值位置发生偏移,该时间偏移量为:
(5)
雷达对目标距离的测量是基于输出峰值出现的时间位置。该偏移量将造成雷达测距误差。由式(5)可知,因多普勒频移引起的测距误差为:
(6)
由式(6)可知,对于同一匀速运动目标,随着距离变化,切换波形(信号脉宽、带宽)时,测量误差会产生变化。
假设雷达工作频率为12 GHz,目标运动速度为200 m/s,使用波形1时,距离-多普勒耦合引起的测距误差为48 m;使用波形2时,该项误差为9.6 m。
依据雷达距离跟踪原理,假设雷达是对距离预测值为中心±τ(τ=1/B)波门内的数据进行恒虚警率(CFAR)检测,以确定目标是否存在。当目标运动至9 km,雷达从波形1切换至波形2时,若不考虑随机误差,脉冲压缩处理后的目标回波中心与距离预测值的距离为48-9.6=38.4 m,即目标回波偏离检测波门中心(距离预测值)38.4 m。此时雷达距离波门宽度计算为±60 m,目标仍在距离波门内,距离-多普勒耦合引起的测距误差减小,所测距离发生跳变。
若目标速度过大,将导致真实目标的回波中心不在检测波门内,雷达丢失目标,如图3所示。

图3 波形切换时测距变化示意图
综上所述,波形切换导致距离跳变的本质在于目标运动引起的多普勒频移使接收到的回波信号在频率上出现偏移,从而产生了距离-多普勒耦合误差,不同波形(信号脉宽、带宽)引起的距离-多普勒耦合误差不同,导致雷达波形切换时所测量目标的距离发生跳变。因此,为保持对目标的稳定跟踪,必须对距离-多普勒耦合引起的距离测量误差进行修正。
3 解决方法研究
关于距离-多普勒耦合误差的修正方法,相关文献均有研究,但存在一定不足[11-13]。采用交替发射正负线性调频信号的方式可以直接消除距离-多普勒误差,但需要增加1套发射接收支路,或者增加工作时序设计的工作量。对原始回波信号的多普勒频移进行补偿时,随着目标方位变化,fd不停变化,需要存储大量匹配滤波系数值,占用较大存储空间。
以某雷达为研究对象,其信号处理过程为数字化处理,具有距离回路、速度回路、角度回路以及自动增益控制(AGC)回路。信号处理系统将处理结果发送给上位机。因此,由信号处理系统在发送处理结果前对距离-多普勒耦合误差进行补偿,可以有效避免上述问题。
具体实现方法是:雷达稳定跟踪目标的条件下,利用已经解算出的目标速度和距离信息,按照公式(6)计算距离-多普勒误差,对测距结果进行修正,作为最终的距离信息。该方法在信号处理末端进行,计算量小,易于实现。信号处理工作过程如图4所示。

图4 进行距离-多普勒补偿的信号处理流程图
需要注意的是,修正距离-多普勒耦合引起的测距误差时应考虑调频斜率的正负。当线性调频信号调频斜率k>0时,修正公式为:
(7)
当线性调频信号调频斜率k<0时,修正公式为:
(8)
式中:R′为修正后距离值;R为修正前距离值。
利用合作目标进行试验验证。工作参数设置为:雷达工作频率12 GHz,波形参数选择同表1。设置合作目标速度为2 000 m/s,分别记录目标距离-多普勒耦合修正前和修正后的测量结果,并与目标真值进行比较,结果如图5所示。距离-多普勒耦合误差修正前后误差统计如图6所示。
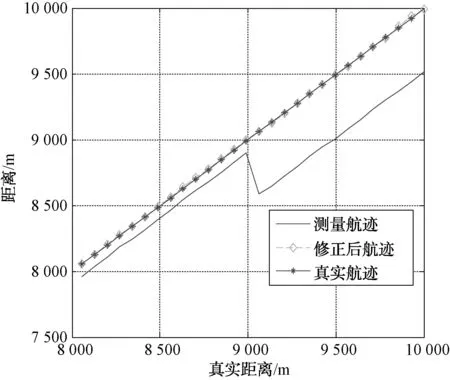
图5 距离-多普勒耦合修正前后的距离误差
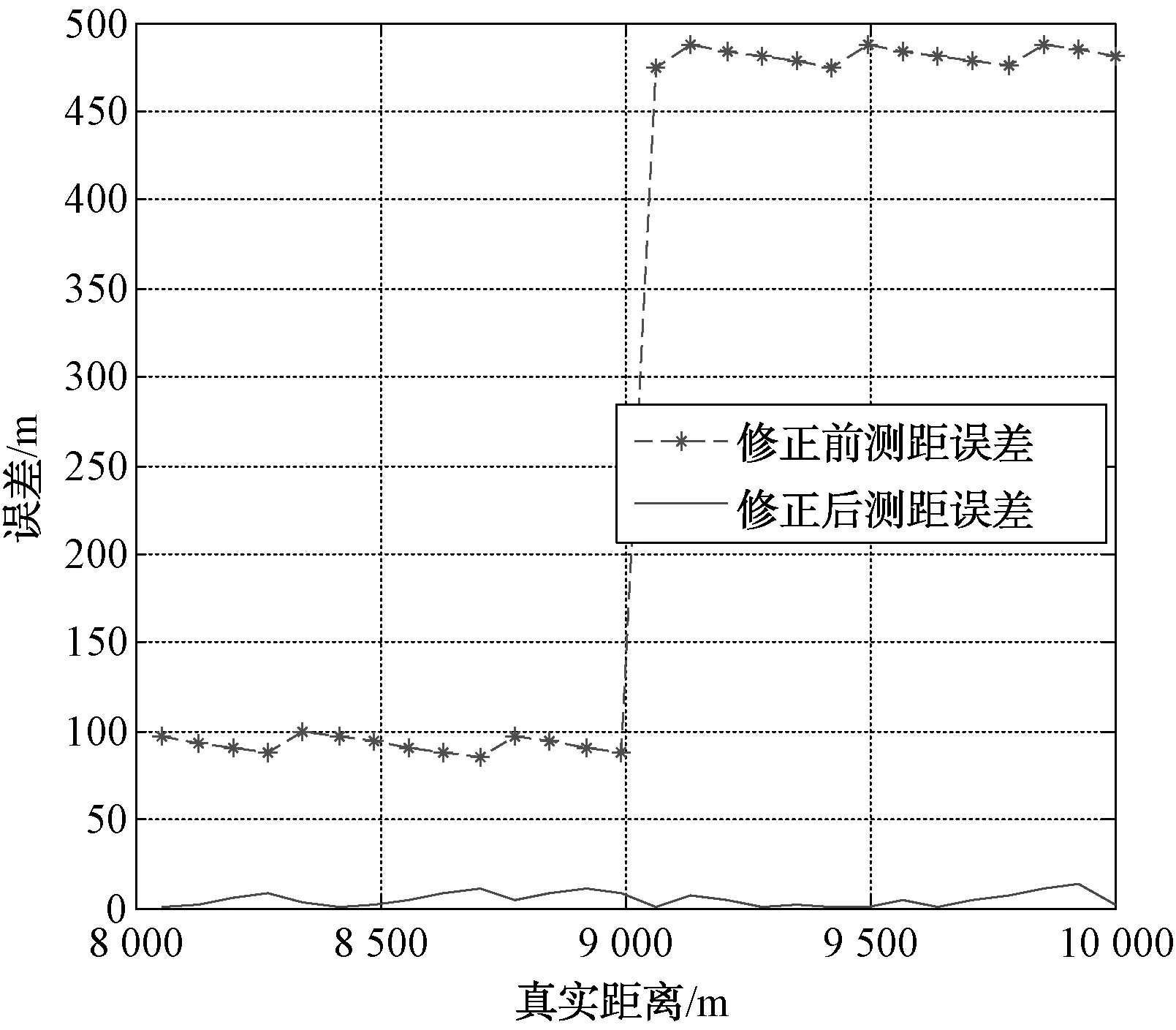
图6 距离-多普勒耦合修正前后误差统计
从图5和图6可以看出,未进行距离-多普勒耦合修正前,距离误差最大可达486 m;进行修正后,距离误差最大为13 m。进行距离-多普勒耦合修正后,波形切换时距离测量值未发生跳变,目标跟踪稳定,且提高了测距精度,证实了该方法的可行性。
4 结束语
本文对采用脉冲压缩体制的雷达在波形切换时距离测量值产生跳变的问题进行了研究分析,导致波形切换时刻距离跳变的根本原因是存在距离-多普勒耦合误差,对距离-多普勒耦合产生的原因及其对脉冲压缩雷达测距的影响进行了研究,提出了一种易于工程实现的距离-多普勒耦合补偿方法,并进行了试验验证,解决了波形切换时距离测量值的跳变问题,减小了测量误差。

