借助几何直观厘清数量关系
冯玉秀
在解决问题的过程中,借助画直观图的方式,将数量关系的精确刻画和空间形式的形象直观密切结合,依托于“形”的支撑来显化数量之间的内在联系,成为解决问题的有效方法之一。因为将数量信息反映在图形上,依托图形能直观地表现数量之间存在的联系,达到化抽象为具体、化隐为显的目的,起着提示获取抽象问题的一些簡单、快捷的解决思路的作用。本文就小学数学教学中,如何培养学生借助“几何直观”厘清数量关系,达到解决问题的目的,谈一些想法。
1.培养学生画图的意识
在数学课堂上,一些学生遇到比较复杂的数量关系,或者是一些纯文字的数学问题时,往往两眼直盯着题目,冥思苦想、一筹莫展。这时可以提醒学生:没有解题思路时,可以反复认真的读题,再根据题目的意思涂一涂、画一画。也许这些涂涂画画会对你有所启示。这里的涂涂画画就是借助几何直观分析问题、解决问题。课堂上,那些有意画图思考的孩子往往在学习中占有优势,抽象能力更胜人一筹。因为示意图画出后,题意就更清楚了,数量关系建构都不在话下。所以所谓的难题也就迎刃而解了。
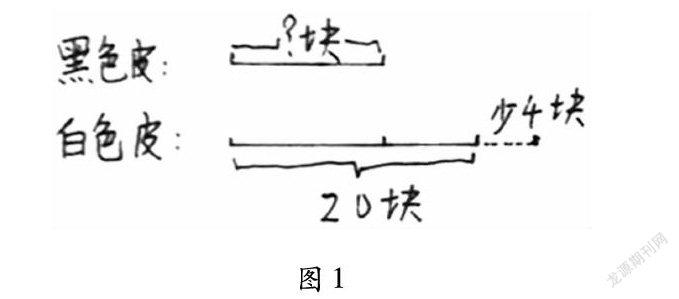
例如,足球上白色的皮都是六边形的,黑色皮都是五边形的。一个足球上白色皮有20块,比黑色皮的2倍少4块。白色皮和黑色皮一共有多少块?学生在做这道题时往往搞不清黑色皮和白色皮块数的关系,所以求黑色皮时会出现以下一些错误:或者或者教学中我这样引导学生画图:首先画什么量?画多长?为什么?再画什么量?又画多长?为什么?先画黑色皮,表示黑色皮的线段长度可以任意画,因为黑色皮是基础量。有了黑色皮才能画白色皮,表示白色皮线段的长度是黑色皮的2倍。(如下图)从图就可以清楚的看出两种量的数量关系:白色皮+4块=黑色皮2。错误也就会大大减少。
我认为,在学生涂涂画画这个过程中,学生在经历合情合理的推导、想象和顿悟;在不断积累知识、积累解决问题的经验和办法;在感受数学学习的策略和思想。
2.教授画图的方法
让“几何直观”促进数学问题解决,是我们数学教学的重要任务之一。我们在教学中要刻意推动“几何直观”,做到让“几何直观”贯穿于我们的数学教学活动之中。在解决问题的过程中,引导学生画图分析,将文字翻译成“图画”。
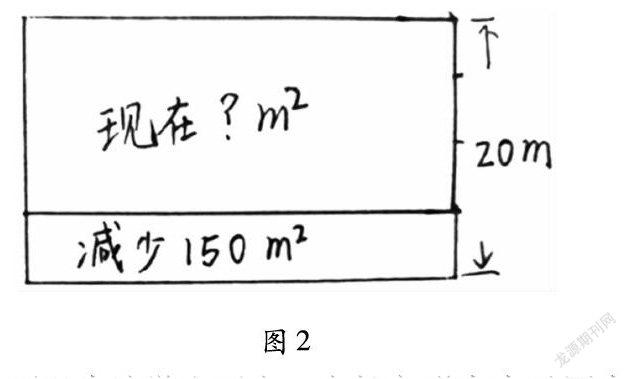
例如,小学数学中经常会有这样的题目“一条公路旁原来有一个宽20米的长方形鱼池。后来因扩建公路,鱼池的宽减少了5米,这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米?”这种纯文字形式呈现的数学问题相对比较抽象,凭空想象很难弄清题意。这时要适时引导学生动手画图,借助图形寻求解决问题的思路。
教学中,可以先让学生画出一个长方形来表示原来的鱼池,然后引导学生思考并表示出宽20米在哪儿?减少的150平方米又在哪儿?要求的问题是图中哪一部分?当学生弄清楚这些问题后,题意自然就一清二楚了。当学生正确解答题目后,教师一定让学生反思画图步骤、画图意义。这样的教学过程,从解决实际问题的需要出发,紧紧围绕利用画图进行直观推理展开,使学生在解决问题的过程中学会了画示意图整理条件和问题的方法,积累了借助图形直观分析数量关系的经验,发展了学生的几何直观能力。
3.亲历画图的过程
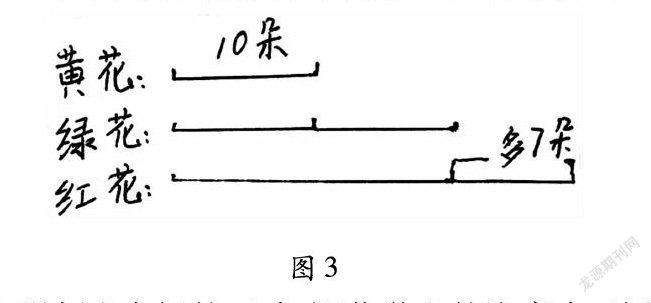
在平时的数学教学中,我们教师采用几何直观教学方法的时候,要加强和学生之间的互动,让学生亲历画图的全过程。比如,在解决这一的题目时“黄花有10朵,绿花的朵数是黄花的2倍,而红花的朵数比绿花多7朵,请同学们告诉教师红花有多少朵?”教师让一位学生在黑板上做出线段图,然后,有些学生发现了一个问题,表示多出的7朵的线段和前面10朵的线段一样长,然后,教师将这表示多出的7朵线段画得短短的一段。学生又表示画的太短了。然后教师让学生思考到底怎样画才是合理的。学生思考后,会发现只要比黄花10朵的线段长度的一半多一些就可以了。教师再根据学生的意见修改线段图。
通过加强师生之间的互动,调节学生的注意力,让学生发现问题、修正线段图,引导学生透过事物表面,发现事物的本质,从而完成具体到抽象的过渡。学生也只有亲历了画图的过程才能真正体会画图意义、掌握画图的方法,从而形成几何直观的能力。才能在以后的解决问题过程中自觉地应用画图来帮助自己解决问题。
当然,“几何直观”是一种策略、一种思想,而不是单纯的技能。很多时候,解决数学问题的思维正是在采用“几何直观”的建构、思考、尝试、表达的过程中得到启发。这对于学生核心素养,培养学生学科能力至关重要。“几何直观”塑造的是学生认识客观世界的思维品质和多元的解释、多元的表达方式。

