高中物理中模型思维能力的培养

童锴

【摘要】  物理是一门以观察、实验为主的学科，物理教学的基本任务是使学生掌握物理学的基础知识和基本技能更重要的是使学生掌握研究问题的方法。而模型的变换对于高中生来说是一个重要的问题，本文中重要从模型变换的障碍和方式两个方面来作一个简单的研究。

【关键词】  模型思维 模型变换 思维定式 表象干扰 等效变换 类比变换

【中图分类号】  G633.7               【文献标识码】  A   【文章编号】  1992-7711（2019）15-131-01

模型就是通过我们对问题现象的分解，利用我们考究得来的机理，吸收一切主要因素，略去一切不主要因素所创造出来的一幅图画。所谓模型思维，就是利用模型达到特定认识目的的思维方式。在物理教学活动中之所以要研究模型思维，是因为它不但是推动物理学进展的重要的思维方式，而且是教好、学好物理课程的重要的思维方式。

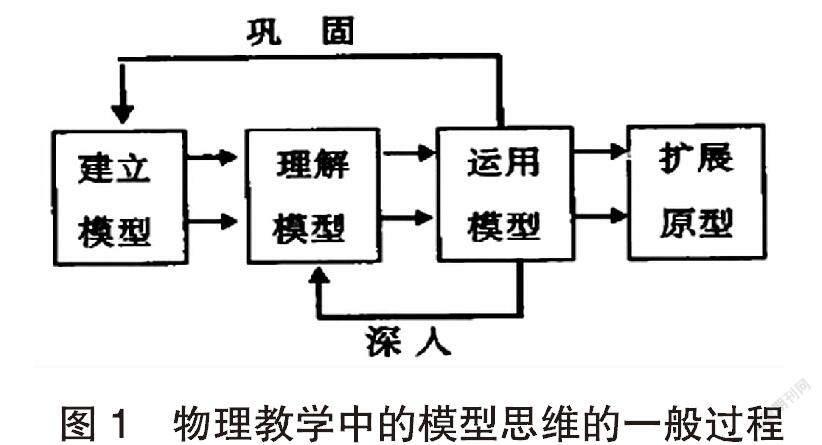
物理教科书中有许多理想化模型，如研究对象的理想化模型有质点、刚体，弹簧振子，单摆，理想气体，匀强电场、点电荷，薄透镜等;物理过程的理想化模型有匀速直线运动，简谐振动，理想气体的等温变化，镜面反射等。物理模型是物理实体的近似反映，实际物体要经过合理的近似处理才能模型化。但是，由于模型突出了事物的主要因素，忽略了次要因素，因此物理模型不但反映了事物的本质特征，而且使研究过程大大简化。因此物理模型教学的一般过程可用下图表示

许多学生反映物理课听起来有趣，做起来（做练习）难。他们的困难，往往不在于记不住某个物理公式，而在于对一个新情景问题不知道该用什么公式。换句话说，就是不善于将一个具体问题转换成某一物理模型，因此，加强中学生模型变换能力的培养对于其模型思维的发展将显得尤为重要。即，模型思维能力的培养重在模型变换能力的培养。

1.模型变换的主要障碍

1.1思维定势

在教学过程中，尤其在建立模型时，教师往往强调了模型的理想化而忽视其可变性，即模型可以灵活变换，广泛运用，使学生在思想上产生模型的绝对化倾向，妨碍了思维的开展。

例l，已知质量是0.99kg的物体M放在光滑圆弧轨道OA的最低点O，质量为m=0.01kg的子弹以100m/s的速度水平击中物体M并留在其中，求物体从开始运动到返回O点所用的时间（圆弧轨道半径为39.2m）。

学生能根据系统碰撞前后动量守恒求出物体获得的速度V。物体获得速度V后沿圆弧轨道的运动是变速曲线运动，题目又未给出弧长或它所对圆心的张角，在中学阶段按常规方法无法求解。但仔细分析物体的受力情况后，不难发现它受重力和轨道的支持力作用完全类似于单摆的受力情况。这就启发我们：能否用单摆模型求解？通过计算知道，物体在圆轨道最高点与最低点的半径夹角，这样，可把物体在圆弧轨道上的运动归结为单摆模型，巧妙地用单摆周期公式求出t=4s。造成学生不会联想到用单摆模型来解的根源在于单摆模型教学中的思维定势，认为单摆总是悬挂着且摆球上只能受到重力和摆线的拉力作用而在最低点附近振动。

1.2表象干扰

学生在分析物理问题时，思维的焦点往往集中在問题的表面现象上，对于陌生的物理模型缺乏辨异识同，无法把知识运用到未知现象中去，即不善于排除表象干扰抓住本质因素，将题中的物理模型与熟悉的物理模型相比较，分析异同并寻找出内在的联系和相同点，建立起熟悉的模型与未知现象的关系。

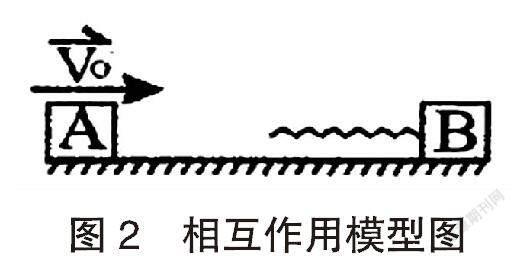
例2.在光滑的水平轨道上有两个半径都是r的小球A和B，质量分别为m和2m，当两球心间的距离大于I（I比2r大得多）时，两球之间无相互作用力：当两球心间的距离等于或小于l时，两球间存在相互作用的恒定斥力F.设A球从远离B球处以速度v0沿两球连心线向原来静止的B球运动。欲使两球不发生接触，v0必须满足什么条件？

该题描述的物理模型与教材中分子球的相互作用，如图2所示，求弹簧的最大势能等，都属于相互作用的问题，所不同的是本题中相互作用的是“恒力”而不是变力。平时用动量守恒和功能关系来解碰撞中压缩过程中的问题训练也不少。学生打不开思路的关键是被题设中的一个抽象的斥力迷惑。若能与熟悉的两物体作完全排弹性碰撞模型类比，并运用其结论，必将触发灵感，启迪思路：两球将接触而未接触时系统损失的动能最大，且损失的动能全部转化为系统的斥力势能，此时刻A、B球应具有相同的速度。

2.模型变换的两种方式

2.1等效变换

等效的思想是物理学研究的基本思路之一，教材中不乏其例，前面例1中介绍的分析方法便是一种等效变换方法。又如：导线电阻为R，做成一个闭合圆环，半径为r，一直导线以速度V运动，环放在磁感应强度为B的习强磁场中，直导线电阻不计，则运动到圆心处的瞬间，直导线中的电流为多少？

当直导线经速度V的运动时，直导线两端会产生感生电动势，由于整个回路是闭合的，故圆环中有感生电流产生。这时，直导线相当于一个电源。这种情况与图所示电路等效，若能作这样等效变换，那么本题就变得简单易解了。

2.2类比变换

物理学中有许多事物或现象之间的关系具有相似性，这就为我们进行类比变换提供了依据。

例3，一长为l的细绳，上端固定，下端拴一质量为m的带电小球，将它置于场强大小为E的水平向右的匀强电场中，当处于平衡时，细线与竖直方向成a角（α≤45°）。如果使偏角由a增大到φ，然后由静止释放，则φ应多大才能使细线到达竖直位置时，小球的速度刚好为零。

本题的原型是重力场中的单摆模型，现在小球不仅受到重力作用，同时还受到电场力作用，若将这两个力合为一个力，则容易判断小球的平衡位置在O点。小球从A点释放后，在A、B之间来回振动的模型若与原型类比，则小球相当于悬挂在一个特殊场中的摆球。由原型的结论推知：小球通过平衡位置O时速度最大，在两振幅位置A、B时速度为零。由于对称性可判定φ=2α.

在模型变换教学中，教师是导游，是引路人，学生则是领略大自然胜境，进而改造自然的主人。这样，简繁有致，逐渐深人，学生的模型变换能力就有效地建立起来。