有理数集的可数性与稠密性应用

祁瑞生，徐大树

（东北大学秦皇岛分校数学与统计学院，河北秦皇岛066000）

1 在数学分析中的应用

1.1 解函数方程的柯西法

函数方程是指含有未知函数的等式，它与代数方程、微分方程不同，并没有普遍的解法，尽管如此，还是有一些经典的方法，如换元法、待定系数法、柯西法等。其中，柯西法基于有理数集的稠密性，是一个重要的求解函数方程的方法。

注1 利用柯西法，还可以求解如下几个经典的函数方程[3]：

注2 例1的结论应用广泛，利用例1的结论可以证明泛函分析中的两个命题。

命题1[2]设V是赋范线性空间，若它的范数则可以在V上定义内积(⋅,⋅)，使得该范数由内积诱导而成。

命题2[2]实赋范线性空间E到E1的连续可加算子必满足齐次性，从而是连续线性算子。

1.2 证明函数不等式

基于有理数集的稠密性，可以证明许多与连续函数有关的命题，利用函数的连续性与海涅定理，可以先研究连续函数在有理点处的性质，进而再由有理数集的稠密性找到有理数数列逼近定义域内任何一个实数，从而得到一般结论。

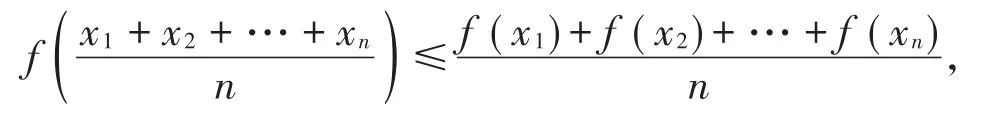
注3 利用与例2证明相似的方法，可以证明：设f(x),g(x)是定义在实数域R上的连续实函数，且对任一有理数r，有则这表明连续函数的取值完全由它在定义域中有理数点处的取值所决定。

注4 例1与例2的证明中都利用了Q在R中的稠密性，即对任一实数r∈R，都存在有理数数列，使得

1.3 构造分析学中的反例

有理数集的可数性与稠密性为构造分析学中的许多反例提供了思路，如有界却黎曼不可积的狄利克雷函数[5]；在无理点连续，而在有理点不连续的黎曼函数[6]。

例3 试构造反例说明以下两个命题均为错误的：

（1）若函数在一点连续，则在该点的某个邻域内每一点都连续。

（2）若函数在一点可导，则在该点的某个邻域内每一点都可导。

解 构造反例如下：令f(x)=x2D(x)，其中D(x)表示狄利克雷函数，即

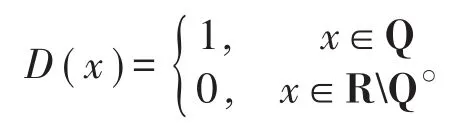
1.4 证明连续函数介值定理的逆定理

定义在连通集上的连续实函数具有介值性，即若f(x)可以取到a和b，则f(x)可以取到a和b之间的任意一个数。反之，具有介值性的函数却未必连续。但利用有理数集的稠密性，可以证明一个介值定理的逆定理。有理数集的稠密性表明任意两个实数之间总是存在一个有理数[7]，利用这一性质，可以证明连续函数介值定理的一个逆定理。

命题3[8]设f(x)是定义在实数集R上的实函数且具有介值性，即对，存在x介于a,b之间，使得f(x)=c。若对任一有理数是闭集，证明：f(x)在R上连续。

证明 用反证法，设x0为f(x)的不连续点，根据海涅定理，存在一个数列满足，但于是存在f(x0)的开邻域使得数列有无限项在该邻域之外，亦即存在的子列使得不失一般性，设由有理数集的稠密性可知存在有理数r使得由介值性可知存在tk介于x0,yk之间，使得故由得，而E是闭集，故x0∈E，所以，这与矛盾。

2 在实分析中的应用

称一维直线E1的子集G为开集，如果它的每个点都是内点。在实分析中，考虑一维直线上有界开集的结构是一个重要的问题，基于有理数集的可数性，证明下面的命题。

命题4[9]一维非空有界开集可以表示成至多可数个互不相交的开区间的并。

证明 设G为一有界开集，可以证明：任取x∈G，存在开区间(a,b)，使得x∈(a,b)，且(a,b)⊂G，a,b∉G[9]。已知G中任意一点x都对应一个开区间(ax,bx)⊂G，当x≠y，对应的开区间(ax,bx),(ay,by)若相交，则必重合。否则，将与ax,ay,bx,by∉G矛盾，从而G可以表示成一些互不相交的开区间的并。由于这些开区间互不相交，由有理数集的稠密性与可数性，可在每个开区间内取一个有理数与这个开区间构成一一对应，这些有理数是至多可数个，从而这些开区间为至多可数个。

3 在点集拓扑中的应用

定义1[10]设X为一个拓扑空间中的点p称为集合A的聚点，如果p任一邻域都包含中的至少一点。A的聚点的全体称为A的导集，记为d(A)。

在拓扑学中有如下经典习题：

例4[10]给R赋予余可数拓扑，即定义R上的拓扑为可数集记Q为全体有理数集合，试求有理数集Q的导集d(Q)。

解 任取x∈R。若x∈Q，下面证明x不是Q的聚点。事实上，取，则可数，所以注意到，从而x不是Q的聚点。若，取，则Bc=Q可数，所以注意到，从而x不是Q的聚点。综上所述，∀x∈R都不是Q的聚点，所以

4 在泛函分析中的应用

先引入度量空间可分性的定义。

定义2[2]设A，B均为度量空间X的子集，如果，则称B在A中稠密。

定义3[2]设X为度量空间，若X存在稠密的可数子集，则称X可分。

有理数集是可数的，从而可以从有理数集出发构造一系列的可数集，例如利用这些构造出的可数集，可以证明一些度量空间的可分性。

利用与例5相似的方法，可以证明下面的例6与例7。

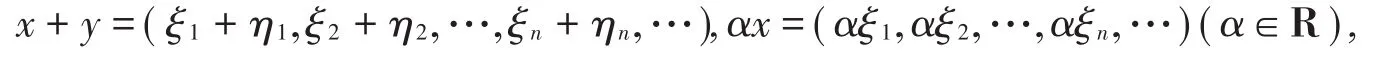
例7 设c为一切收敛实数列构成的集合，在c中定义线性运算如下：其 中在 c 中 定 义 范 数 为其 中 x=设d(x,y)为范数诱导出的度量，即证明c在度量d下可分。

下面的例8在研究可分希尔伯特空间的结构时有着重要的作用。

例8 设V是实内积空间，若V中存在完备的规范正交系，则V可分。

5 结束语

有理数集的可数性与稠密性在本文的例题与命题中得到充分的运用，从有理数集的可数性与稠密性出发，可以将相关的结论推广到更一般的拓扑空间上。