数值分析课程中Lagrange插值法的教学与设计

陈素根

（安庆师范大学数学与计算科学学院，安徽安庆246133）

“数值分析”是高等院校数学类专业的重要基础课程，同时也是很多理工科专业的主要公共课之一，它主要研究计算机求解各种数学问题和模型的数值计算方法及其理论与软件实现[1]。“数值分析”课程是一门具有很强实践性的数学课程，不仅具有数学高度抽象性特点，而且其理论体系构建、算法设计等思维方式也具有鲜明特点，注重数值方法和解决实际问题的工程思想，在意方法的精确性和计算效率之间的平衡[2]。然而，传统的数值分析课程教学中存在一些问题，为此，诸多学者对数值分析课程教学方法及实验教学进行了探究[3-6]。

插值方法是数值分析课程中最基本的内容之一，主要研究用简单函数为各种离散数据建立连续的数学模型代替原有的复杂函数。然而，在教学过程中往往注重插值方法原理的讲解，再加上实验环节不够重视，使得学生不能熟练掌握插值方法，从而严重影响了数值分析课程中后续内容的学习效果以及学生对数值分析课程的学习兴趣。实际上，插值方法在工程外观设计、经济数据分析与处理、图形图像处理等方面都有应用，有广泛的实际应用背景。尝试通过实际问题驱动理论教学并结合实验精心设计加以巩固和提升，不仅有利于学生深刻理解插值方法的原理，而且有利于将理论与实际相结合，切实提高学生的实践能力和创新能力。因此，系统设计插值方法的教学过程对数值分析课程的整体教学有一定的意义。本文针对Lagrange插值方法的理论教学和实验教学进行设计和探讨。

1 Lagrange插值法

在插值函数中，多项式函数由于简单、实用而被广泛使用。多项式插值问题概述如下：给定函数f(x)在n+1个互异节点xi(i=0,1,2,…,n)处的函数值及其导数值

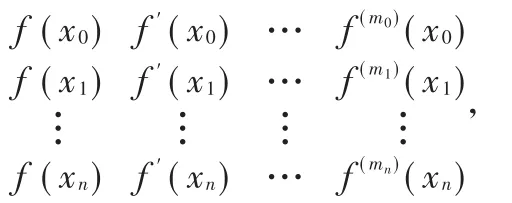
其中mi为自然数，插值条件共有个。插值问题就是求不超过N-1次的代数多项式函数H(x)，使其在上述节点处与函数f(x)有相同的函数值和各阶导数值，即

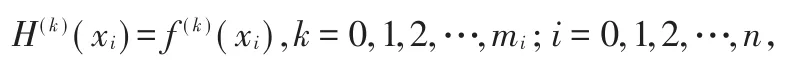
当mi全为零时，即插值条件没有导数插值条件时，上述插值问题即为拉格朗日(Lagrange)插值或牛顿(New ton)插值或样条(Spline)插值；当mi不全为零时，上述插值问题即为埃尔米特(Herm ite)插值。

具体而言，n次Lagrange插值多项式为

其中yj=f(xj)为插值函数值，lj(x)为拉格朗日基函数：

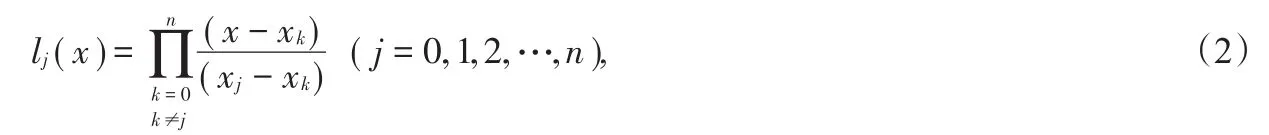
显然，基函数满足条件：

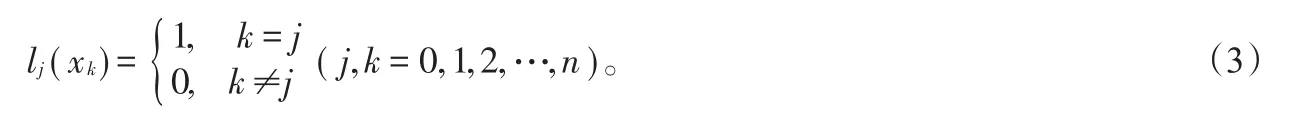
2 Lagrange插值法的理论教学设计

第一步，问题驱动。结合插值法在实际问题中的应用，讲述插值法的提出、发展以及研究现状，让学生了解插值法的应用背景，激发学生学习的兴趣。许多实际问题中都用函数来表示某种内在联系或规律，但不少函数只能通过实验和观测来了解。比如，结合经济数据处理与预测讲解插值问题的提出；结合现代机械工业设计中利用计算机程序控制加工机械零件问题讲解插值函数问题，根据设计可以给出零件外形曲线的某些型值点，利用插值方法计算加工时走刀的方向和步数。通过讲解Lagrange插值方法的发展史，让学生了解该方法的来龙去脉；通过实际问题驱动的方式讲解Lagrange插值在实际问题中的应用，让学生理解该方法的应用背景，让枯燥复杂的理论和原理推导稍微有趣一点，便于学生理解。

第二步，递进式教学。首先，在插值问题提出的基础上，立刻给出多项式插值的存在唯一性定理和插值余项估计定理。此时仅注重结论，不过分追求理论证明，只要求学生明白满足插值条件的多项式是存在唯一的，而且插值效果的好坏是可以用插值余项进行估计的。事实证明，在教学过程中一味强调这里的理论证明过程，让很多学生学习兴趣骤减，直接影响教学效果。其次，教学内容由易到难，从学生们最熟悉的一次函数和二次函数讲起，如：互异的两点唯一确定一条直线，互异的三点唯一确定一条抛物线。这样，让学生感觉到这些内容并不陌生，就不会畏惧新内容的学习。此时，通过对所构造的一次函数和二次函数的化简，得出关于函数值的组合表达式，进一步引出基函数的概念，从而为讲解Lagrange插值问题打好基础。关于Lagrange插值，重点讲清（2）式的构造思想，然后从二次、三次基函数逐渐向高次基函数归纳和推广，并配合Matlab编程绘制基函数的图形，这样学生就可以更好地理解这样构造的多项式为什么就是插值的。在此基础上，结合（1）式讲清楚编程实现的流程图，通过不断增加插值节点的个数，举例让学生体会到Lagrange插值的缺点。最后，分析讨论Lagrange插值的优缺点，顺利过渡到后续内容的讲解。虽然Lagrange插值的公式结构整齐紧凑、理论分析方便，然而在计算中，当插值点增加或减少一个时，所对应的基函数就需要全部重新计算，插值公式也会变化。为克服这些缺点，就需要构造其他插值方法，为讲述New ton插值法的构造做准备。此外，当插值节点个数比较多的时候，构造的Lagrange插值多项式一般次数会很高，利用Matlab绘制插值曲线图形说明该方法的数值不稳定，从而解释高次Lagrange插值的龙格现象，为过渡到分段线性插值问题作铺垫。总之，通过对Lagrange插值方法优缺点的分析，自然过渡到新内容的讲解，结合Matlab绘制图形让算法效果可视化，这种递进式教学设计，有利于学生对Lagrange插值方法全面理解和掌握。

第三步，将科研融入教学。Lagrange插值是常用的插值方法，在工程问题中有重要应用。但其本质是多项式插值，而且高次多项式插值会出现震荡现象。事实上，（1）式可以归结为在多项式函数空间Γ={1,x,x2,…,xn}中构造多项式：

利用插值条件，构造相应的线性方程组，求解出待定系数a0,a1,a2,…,an。简单推导，很容易得出（3）式对应的插值问题转化为求解线性方程组，再将求解出的待定系数a0,a1,a2,…,an代入（3）式即可，

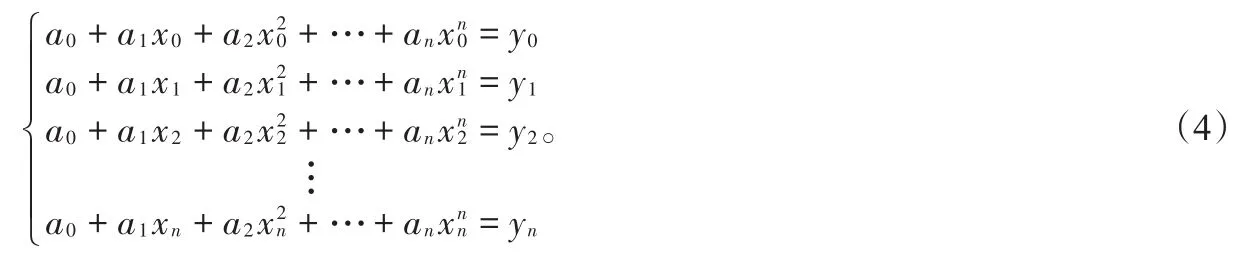
这样，插值问题的存在唯一性问题就转化为线性方程组解的存在唯一性问题，此时再补充讲解理论证明，就更便于学生理解和接受了。下面结合一个具体的例子进行讲解。一方面通过（1）式构造Lagrange插值多项式Ln(x)；另一方面通过（4）式求解待定系数，再带入（3）式得插值多项式Pn(x)，比较Ln(x)和Pn(x)的结果进一步验证多项式插值的唯一性。

例 给定插值节点x=[0,1,2,4];y=[1,9,23,3]，利用（1）式构造Lagrange插值多项式L3(x)和利用（3）式构造插值多项式P3(x)。

解：先利用插值节点构造3次Lagrange基函数如下：

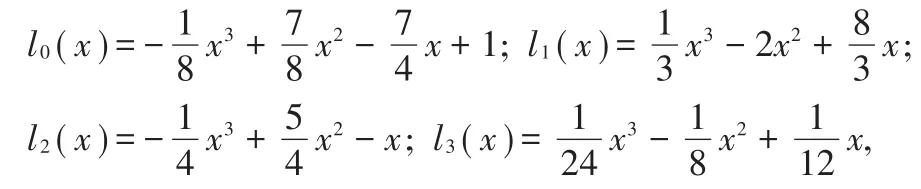
带入（1）式，得3次Lagrange插值多项式L3(x)如下：

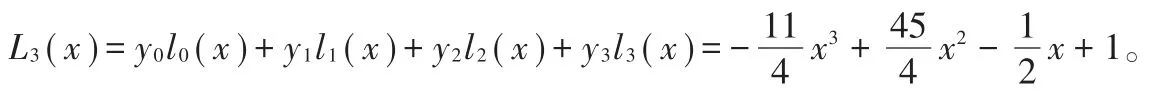
再利用插值条件得到线性方程组如下：

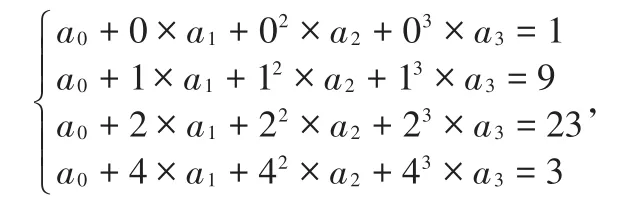
如果仅仅这样就结束课程讲解，就显得意犹未尽，为此进一步讲解插值余项估计问题，从插值余项公式分析为何会出现高次多项式插值的龙格现象，又该如何克服龙格现象？为此，介绍两种改进的Lagrange插值法[7-8]。将基函数（2）式改写如下：

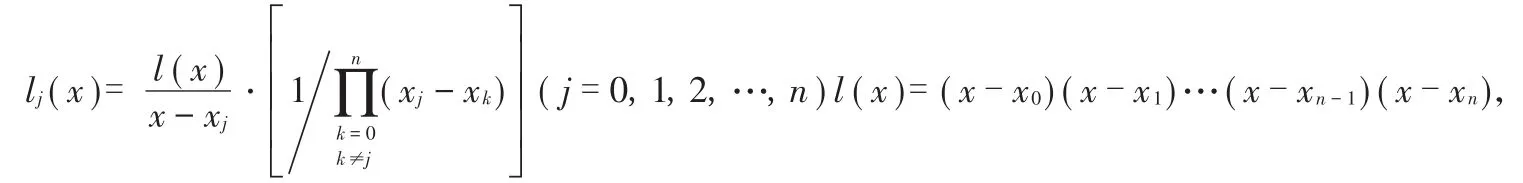
这样就得到了一个改进的Lagrange插值公式，（5）式就是重心Lagrange插值公式（第一型）。它的优点是当插值节点个数增加一个时，将每个wj都除以(xj-xk+1)就可以得到新的重心权wk+1，比重新计算每一个基函数的复杂度降低一个量级。此时，将（5）式用来对g(x)≡1进行插值，可以得到：

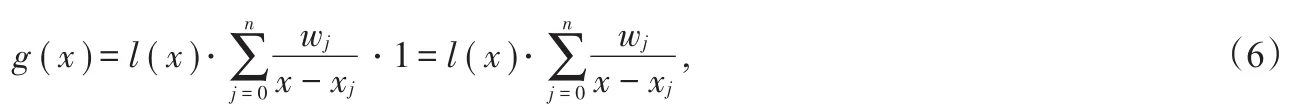
于是，结合（5）式和（6）式，简单计算得：

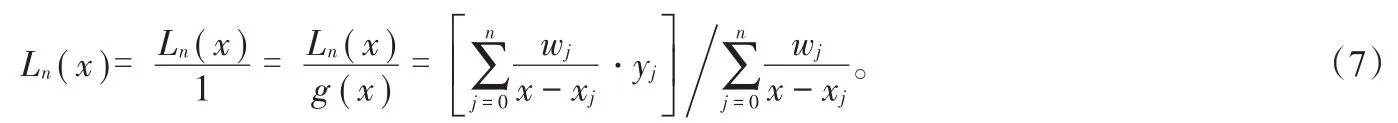
这样就得到了另一个改进的Lagrange插值公式，（7）式就是真正的重心Lagrange插值公式（第二型），它不仅继承了第一型（5）式容易计算的特点，而且在计算中无需再计算l(x)。另外，如果结合切比雪夫节点进行插值的话，可以很好地模拟给定的函数，达到极好的数值稳定性，克服多项式插值的震荡现象。这样不断地拓展Lagrange插值多项式的内涵，层层推进，将科研的思想融入教学过程，同时可以介绍一下如何通过中国知网、谷歌学术等方式查阅参考文献，引导学生主动学习和探索，激发学生参与科研的热情，培养学生的创新能力。除此之外，还可以提出一些问题让学生思考，如：能否在多项式函数空间之外的函数空间构造插值多项式呢？比如在三角函数空间Γ1={1,sin x,cos x,sin2x,cos2x}、代数三角混合函数空间Γ2={1,x,sin x,cos x}或Γ3={1,x,x2,sin x,cos x}等函数空间，正面引导学生在不同函数空间构造插值多项式，鼓励学生动手构造一些新型的插值多项式，尝试解决工程中圆锥曲线精确表示问题是有意义的。总之，将科研的思想融入到教学中，可以培养学生的科研思维和独立思考能力，为今后的科研和学习奠定基础。

3 Lagrange插值法的实验教学设计

很多学校开设数值分析课程中往往比较重视理论的教学，花费较多的时间来讲解插值方法的理论，却忽视了实验教学的开展或者没有认真开展。过多的讲解插值理论，往往会让学生难以理解，从而认为数值分析课程太难，产生放弃学习这门课程的念头。事实上，实验教学可以非常直观的展示插值法的效果，让枯燥的课堂理论教学变得生动有趣。为此，有必要对实验教学过程进行合理的设计。

实验1 Lagrange插值基函数图形的绘制。

实验目标是实现任意次Lagrange基函数图形绘制。考虑到学生实际的编程能力，所以先从二次和三次的Lagrange基函数开始绘制，利用程序1-1可以简单实现二次Lagrange基函数的绘制，效果如图1所示。稍微修改程序1-1就可以实现三次Lagrange基函数的绘制，效果如图2所示。这样让学生感觉挺简单的就可以观察效果，从而主动去动手编程。

程序1-1 二次Lagrange基函数图形绘制

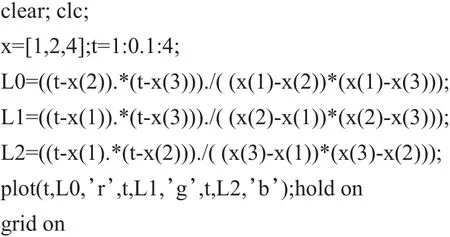
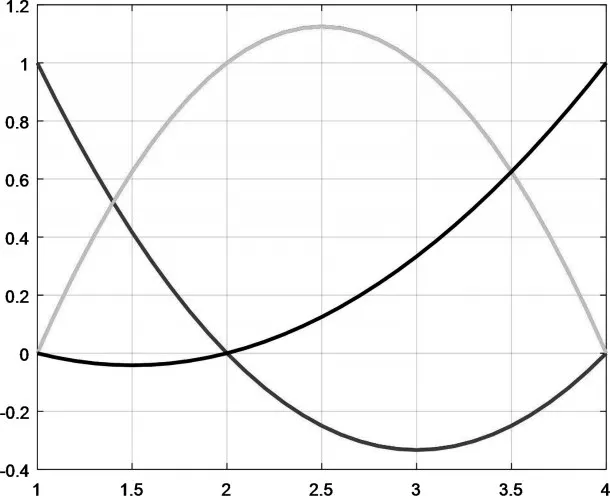
图1 二次Lagrange基函数图形

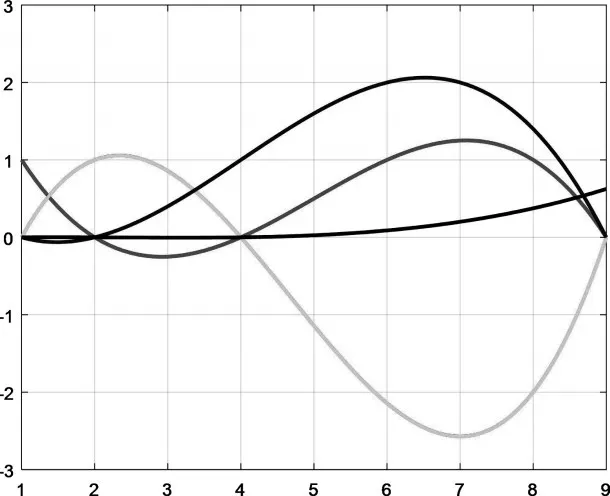
图2 三次Lagrange基函数图形

这些程序非常简单就可以实现，但可以发现一个问题：如果插值节点个数较多时，编写基函数Lj就会变得非常麻烦，显然不能一直这样进行下去。此时，再让学生思考如何绘制任意次Lagrange基函数的图形，通过建立子函数Blending_Function来实现，程序1-2实现了10次Lagrange基函数图形的绘制，图3给出了均匀节点x=[0,1,2,3,4,5,6,7,8,9,10]的10次Lagrange基函数图形，图4给出了非均匀节点x=[0,1,3,4,6,8,9,10,13,14,15]的10次Lagrange基函数图形。这样，只要改变插值节点x的输入，利用程序1-2可以实现任意次基函数图形绘制。通过这种递进式实验设计，由易到难，让学生理解Lagrange基函数的构造方式及其优缺点，培养学生通过函数调用实现编程的能力。同时，在程序实现过程中通过pause命令使得在绘制每一个基函数图形的过程中停顿一会儿，有利于学生观察相应基函数的图形，通过仔细观察基函数的图形来理解高次Lagrange插值为什么会出现龙格现象。

程序1-2 n次Lagrange基函数图形绘制

图3 均匀节点10次Lagrange基函数图形

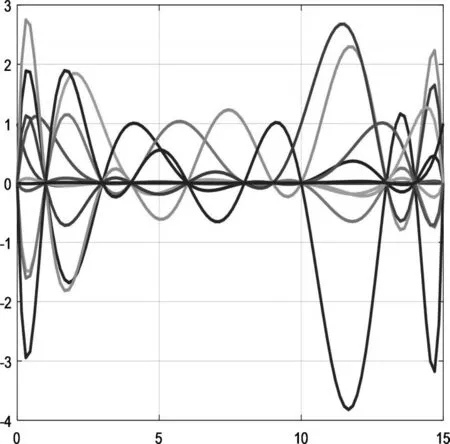
图4 非均匀节点10次Lagrange基函数图形

实验2 Lagrange插值曲线的绘制。

这个实验的目标是实现Lagrange插值曲线绘制。先分析Lagrange插值表达式（1），发现实现图形绘制的主要有两个问题：一个是基函数计算，另一个是求和计算。在此基础上，图5给出了Lagrange插值算法实现的流程图5。

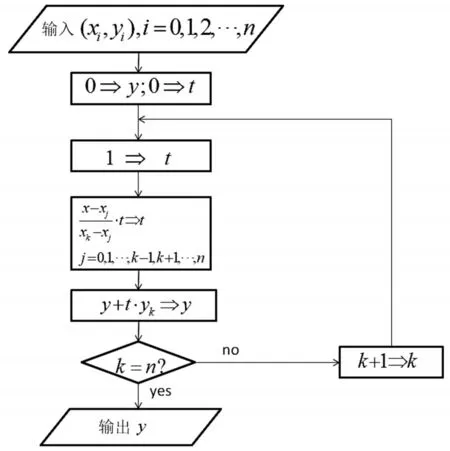
图5 Lagrange插值算法流程图

程序2-1 Lagrange插值曲线绘制

根据流程图，程序2-1实现了Lagrange插值曲线的绘制，然后通过改变插值节点序列x和y的输入，运行程序2-1可以不断实现Lagrange插值曲线的绘制，比较实验结果来观察是否出现震荡现象。图6左图给出了输入x=[0,1,4,9,16,25,36,49,64]，y=[0,1,2,3,4,5,6,7,8]时的实验结果，右图给出了输入时的实验结果。

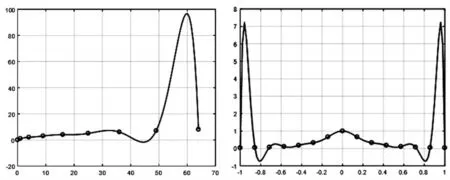
图6 Lagrange插值曲线图形

观察图6结果不难发现，Lagrange插值多项式出现了震荡现象。为此，针对图6右图中的输入函数，选取切比雪夫点，其对应的重心权为取n=14，利用切比雪夫点代替原始输入点x，再利用改进的Lagrange插值公式（7）进行实验，程序2-2实现了插值曲线绘制，图7给出了实验结果。观察实验结果，并与图6中右图进行比较，显然已经没有出现插值的震荡现象了。此时，再次选取n=50，重新利用程序2-2实现50次重心Lagrange插值，图8给出了实验结果，进一步说明了改进的Lagrange插值是可以克服多项式插值震荡现象的。

程序2-2 重心Lagrange插值曲线绘制

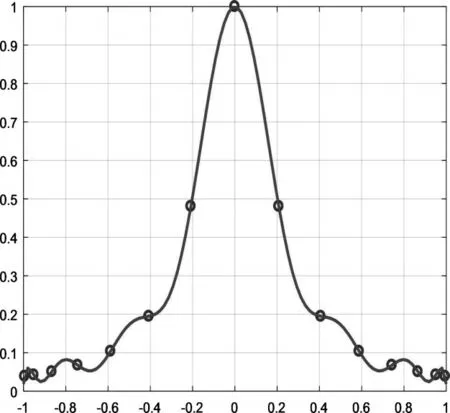
图7 14次重心Lagrange插值曲线图形

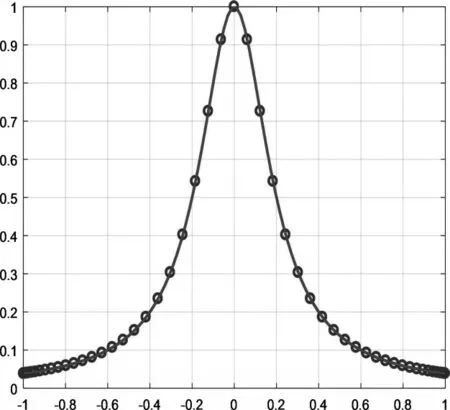
图8 50次重心Lagrange插值曲线图形

4 结束语

数值分析课程是一门具有很强理论性与实践性的课程，理论教学与实验教学必须密切配合才能让学生更容易理解和掌握。通过对Lagrange插值方法的理论教学与实验教学进行精心设计，有利于学生系统掌握Lagrange插值方法的原理和应用背景，不仅为学习数值分析后续内容打下良好基础，而且可以激发学生学习这么课程的学习兴趣，培养学生的动手实践能力和创新能力。