多项式拟合的尺度不变特征变换改进算法

薛理，杨树文，马吉晶，刘燕

(1.兰州交通大学 测绘与地理信息学院，兰州 730070；2.甘肃省地理国情监测工程实验室，兰州 730070)

0 引言

目前，图像匹配算法通常分为两大类[1]。一类是基于像素的匹配算法[2-7]，该类算法根据图像的灰度进行匹配，匹配精度高，但计算量大，而且对图像非线性形变，光照和尺度变化的鲁棒性不强。另一类是基于特征的匹配[8-15]，该类算法需要提取图像上的特征点，然后对特征点进行比较，来实现图像的匹配，计算量相对较少。其中，David Lowe[11-12]于1999年提出尺度不变特征变换(scale-invariant feature transform，SIFT)匹配算法非常具有代表性。由于SIFT算法能够对图像旋转、尺度缩放和亮度变化保持不变性，同时对视角变化、仿射变换、噪声也保持一定程度的稳定性，因此使用较为广泛。Mikolajczyk和Schmid[16]进一步对各种匹配方法进行比较，表明SIFT算法具有非常强的鲁棒性。然而，相关研究表明[17-18]，SIFT算法计算复杂，内存消耗大，当图像较大时算法运行时间较长。为此，学者们对该问题进行了大量卓有成效的研究[19-21]。如Ke和Sukthankar[17]提出的基于尺度不变特征变换的主成分算法(principal components analysis based on representation for local features，PCA-SIFT)，即利用主成分分析归一化权重直方图来代替SIFT算法中平滑直方图，并对SIFT描述符进行降维，从而降低计算量，提高图像匹配速度。Mikolajczyk和Schmid[18]提出的梯度位置方向直方图算法(gradient location and orientation histogram，GLOH)，利用对数极坐标分级结构同心圆来降低算法的复杂性，提高算法效率。刘佳等[19]对图像进行多分辨率小波变换，去除高频成分，采用“回”字形双层方邻窗将特征点邻域区域划分成四部分，建立32 维特征点描述符向量，从而提高匹配精度和效率。程德志等[20]利用准欧氏距离代替欧氏距离作为特征描述符之间的相似性度量来提高SIFT特征匹配效率。

然而，上述改进算法多以照片为研究对象，针对高分辨率遥感影像的研究较少，二者之间在算法精度和效率上存在较大差异。由此，作者通过实验对比分析，发现采用二次多项式能够较为理想地拟合影像直方图；对关键点进行初步筛选时，单一系数筛选较为合适，且最合适的系数为二次多项式的二次项系数；关键点初步筛选占比函数(key-points preliminary filtering proportion function，KPFPF)能够在保证较高的匹配准确率的前提下，明显地提高算法匹配效率。因此，本文提出一种基于高分辨率遥感影像的多项式拟合的SIFT改进算法。

1 算法设计

1.1 SIFT算法简介

SIFT算法主要由4个部分组成：尺度空间极值点检测、关键点精确定位、关键点方向确定和关键点描述符生成。

首先，使用不同的σ(正态分布标准差)对原始影像进行高斯模糊，形成高斯金字塔。然后，每层金字塔中相邻影像相减，形成高斯差分金字塔。其次，将高斯差分影像中每一个像素与周围相邻 8个像素和上下对应9×2 个像素进行对比[12，20]，寻找极值点。

上述检测的极值点为离散空间的极值点，这些极值点位置并不精确，因此需要通过三维二次函数来精确确定极值点的位置，去除低对比度和边缘响应的极值点，形成关键点。

为了使描述符具有旋转不变形，需要给每个关键点分配一个局部方向。首先，统计关键点领域窗口内的像素值梯度和方向[20]。由于距离关键点越远的像素，对关键点的影响越小，因此需要对梯度进行高斯加权。其次，将0～360°平均分成36 分，每份10°，生成方向直方图，以直方图最大值为关键点的主方向。同时为了增加算法的鲁棒性，保留主方向峰值的80%的方向为副方向。

按照关键点的方向对关键点领域区域进行旋转，以确保旋转不变形。然后，选取关键点周围8×8 窗口区域，将该区域分为4×4 个子区域，计算每个子区域8 个方向的梯度，共128 维向量。最后，为了去除光照变化的影响，需要对128 维向量进行归一化处理。

1.2 图像直方图分析

遥感影像直方图能够有效反映图像灰度的分布规律、亮度值分布范围、峰值的位置、均值以及亮度值分布的离散程度等特征。由此，论文通过对高分一号(GF-1)、高分二号(GF-2)、资源三号(ZY-3)和快鸟影像(QB-2)的灰度直方图进行分析，发现直方图大体呈瘦钟形分布，如图1所示(图中横坐标代表像素值，纵坐标代表像素数量)。

图1 影像直方图

1.3 二次多项式拟合直方图

论文采用C#语言和地理空间数据抽象库(geospatial data abstraction library，gdal)，利用编程的方式逐像素地读取遥感影像数据，并将数据归一化到0～255，然后统计0～255中每个像素值的频率，最终生成散点图。

通过实验得出使用二次多项式拟合散点图能较为理想地反应散点图的整体趋势，进而间接反映图像像素值的整体特征，如图2所示，图中红线是拟合曲线。

图2 二次多项式拟合

二次多项式拟合公式如公式(1)所示。

y=a0+a1x+a2x2

(1)

式中：a0、a1、a2为二次多项式的系数；x为像素值；y为像素值数量。

1.4 标准差

标准差能够反应组内个体间的离散程度，因此，利用标准差可以反映遥感图像像素值的整体离散特性。标准差的计算公式为：

(2)

式中：σ’为标准差；n为所有像素的数量；xi为第i个像素的值；μ为像素平均值。

1.5 系数分析

1)系数选取。通过上述分析发现，二次多项式函数和标准差都能够反应局部区域像素值的整体特性。因此，在图像B的所有关键点中寻找图像A中某关键点的匹配点之前，论文采用二次多项式系数和标准差对图像B中所有关键点进行初步筛选，然后，再用关键点128 维向量进行匹配。

为了能更加直观地分析实验结果，对算法的耗时、匹配点数量和匹配正确率[10]进行统计，以曲线图的形式进行显示，如图3～图6所示。正确匹配率如公式(3)所示。

(3)

式中：C代表正确匹配率；cm代表正确匹配的关键点数量；fm代表错误匹配的关键点数量。

图3至图6中时间比代表关键点初步筛选后的算法时间与SIFT算法时间的比值，预选点占比代表关键点初步筛选点的数量占图像B中所有关键点的比率，匹配点数量代表关键点初步筛选后的算法关键点匹配数量，正确率代表正确匹配率。

图3 平移匹配结果

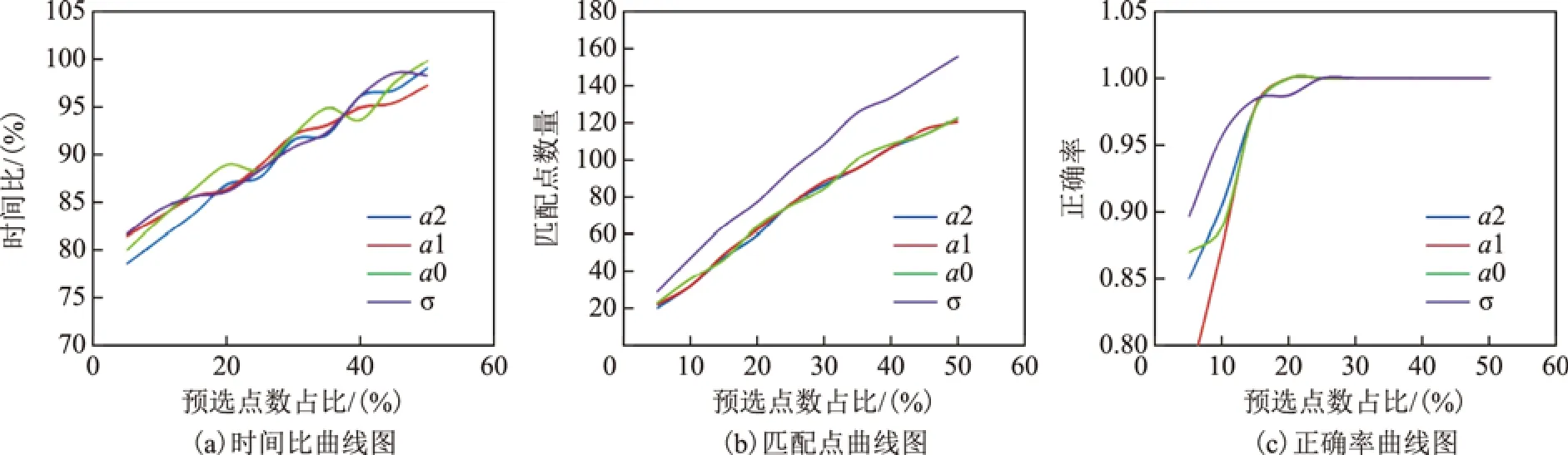
图4 旋转匹配结果

图5 缩放匹配结果

图6 模糊匹配结果

通过分析图3至图6，可以得出以下结论：①平移、旋转和缩放结果的时间比曲线和匹配点曲线大致呈线性分布，正确率曲线大致呈对数分布。②系数a0、a1、a2和σ’的平移、旋转和缩放结果的匹配点相差不大，因此采用多个系数联合对关键点进行初步筛选的方式和单个系数筛选效果类似。③在系数a0、a1、a2和σ’的正确率曲线中，a2正确率收敛到1，预选点占比最大为20%。a1正确率收敛到1，预选点占比最大为25%，a0和σ’的正确率在缩放结果中达不到100%。因此采用系数a2和a1来初步筛选关键点较为合适。④在平移、旋转和缩放结果中，系数a1和a2的时间占比大致相等，然而在模糊结果中a1的时间占比明显大于a2。

综上所述，采用单一系数a2对关键点进行初步筛选较为合适。

2)关键点初步筛选占比分析。虽然上述分析确定了关键点筛选的系数，但是关键点的筛选数量的问题并没有解决，因此接下来主要分析关键点初步筛选的比例。论文选择GF-1、GF-2和QB-2影像中的7张图像，分别对每张图像做平移、旋转、缩放和模糊处理，实验结果如图7所示。

当初步筛选结果的匹配点数量占原算法的1/5左右时，匹配点数量足够，匹配准确率高，同时耗时少。因此以原SIFT算法1/5左右匹配点数来限定初步筛选结果的匹配点数量，来观察初步筛选点占比，即初步筛选关键点占图像B关键点数量的比例。

根据上述标准对图7中的图像进行匹配。对匹配结果进行分析，发现初步筛选关键点占比与图像B关键点数量的相关性较为明显，因此对初步筛选关键点占比与图像B关键点总数进行统计，生成散点图，如图8所示。

图8 初步筛选散点图

图中，横坐标代表图像B关键点数量，纵坐标代表初步筛选关键点占比。从图中可以发现，散点大致呈幂函数分布，因此用幂函数拟合这些散点，拟合曲线如图中红线所示。从图中可以看出拟合效果较为理想，因此关键点占比与图像B关键点数量之间的函数，如公式(4)所示。

y=0.172 5×x-0.129

(4)

式中：x代表图像B关键点的数量;y代表初步筛选关键点占比。

2 算法模型

根据上述原理，本文提出一种基于高分辨率遥感影像的多项式拟合的SIFT改进算法，流程图如图9所示。

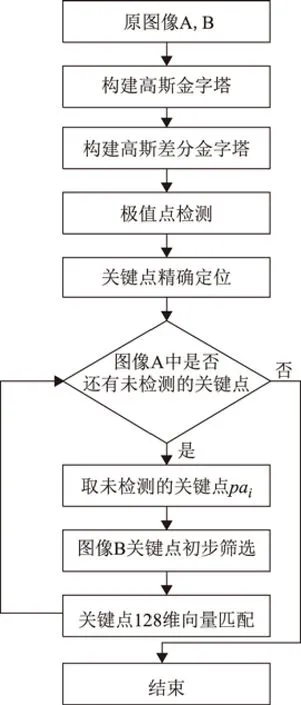
图9 算法流程图

具体步骤如下：

①采用高斯函数对原图像A和B进行模糊，生成高斯金字塔。然后每层金字塔相邻图像相减生成高斯差分金字塔；

②在高斯差分金字塔中寻找极值点，并采用三维二次函数精确定位关键点；

③统计高斯金字塔中每个关键点周围领域窗口的像素值，生成直方图，并利用二次函数进行拟合，获得系数a2；

④取出图像A中的关键点ki，根据初步筛选占比函数，利用系数a2对图像B中的关键点进行初步筛选。然后利用128维向量计算欧式距离最近的2个点，如果次近邻点欧式距离小于最近邻点的0.49倍，则该2个关键点相互匹配，否则ki在图像B中没有相互匹配的关键点。重复上述过程直到图像A中所有关键点遍历一遍，算法结束。

3 实验与分析

实验选取位于甘肃省兰州市的GF-1影像，影像大小为800 像素×600 像素，如图10(a)所示。对该影像进行平移、旋转、缩放和模糊处理，处理结果如图10(b)所示。采用文献[12]提出的SIFT算法和论文改进算法对图像10(a)和图10(b)进行图像匹配，实验结果分别如图10(c)和图10(d)所示。

从图10中容易得出改进算法相互匹配的关键点分布均匀，且关键点之间的距离较远。原SIFT算法关键点较为密集，且存在大量距离较为接近的关键点。

为了验证算法的鲁棒性，本文又分别对GF-2、ZY-3和QB-2进行实验，以GF-2影像为例，实验结果如图11所示。

为了能直观地比较论文改进算法与原算法的匹配精度，统计GF-1和GF-2匹配结果的匹配点数，匹配准确率和算法时间，如表1所示。

从表1容易得出：①GF-1和GF-2的改进算法匹配点数分别占SIFT算法匹配点数的17.1%和22.3%；②改进算法的正确匹配率平均为0.986%，SIFT算法的正确匹配率平均为0.998%，2种算法的正确匹配率大致相等；③GF-1和GF-2的改进算法时间与SIFT算法时间的比值分别为0.551和0.565。

通过上述分析得出：改进算法的匹配点分布均匀，其匹配点数占SIFT算法的1/5左右，改进算法的匹配准确率与原算法大致相等，同时改进算法能够明显加快算法的时间效率。因此改进后的算法能够在保正较高匹配准确率的前提下，明显提高原算法的匹配效率，适用于遥感影像匹配。

图10 GF-1影像匹配结果

表1 关键点匹配结果统计表

4 结束语

本文提出一种SIFT改进算法，该算法能够实现整体粗匹配，局部精匹配相结合的方式对关键点进行匹配，提高了算法效率。由于SIFT算法中关键点描述子计算复杂，导致算法计算量大，耗时长。虽然本文对该算法进行改进，加快了算法效率，但计算时间依然较长。因此在今后的研究中希望分析出一种更为简单的关键点描述子，从而提高算法的实时性和适用性。