中国夜间灯光与建设用地碳排放关系实证分析

，

(1.甘肃农业大学 管理学院，兰州 730070；2.甘肃农业大学 资源与环境学院，兰州 730070)

0 引言

夜间灯光数据已经广泛应用于社会经济因子估算与经济活动监测[1-5]、城镇信息提取[6-8]、自然灾害评估[9-10]以及生态环境评价[10-11]等研究之中。且自Elvidge与Raupach等人发现夜间灯光数据与碳排放存在相关关系以来[12-13]，不少学者通过夜间灯光数据对碳排放进行估算。相关研究按回归模型可分为两大类：一类是传统回归模型，利用最小二乘法对碳排放量进行估算[14-15]；另一类是空间回归模型，由于能源消费碳排放具有显著的空间相关性[16-18]，所以不少学者利用SLM模型或者时空地理加权模型对碳排放进行测算[19-21]。然而，尽管随着研究的深入，夜间灯光数据在估算碳排放方面的潜力不断被发掘，但目前尚无相关研究对二者是否存在关系，若存在关系，又存在何种关系的问题进行探讨，而厘清二者是否真的存在关系，二者存在何种关系是进行碳排放量估算理论基础。

作为反映经济增长与环境压力之间的一种长期关系的库兹涅兹曲线[22]，其始于1955年美国经济学家西蒙·库兹涅茨提出的库兹涅兹曲线理论[23]，而后由格鲁斯曼和克鲁格正式提出[24]。如今已广泛应用于碳排放与城市扩张[25]、经济发展[26-27]、城市化[28-29]之间的关系研究之中，并取得了丰富的成果。另外，不同类型的土地在碳排放过程中的作用不同，建设用地作为人口、建筑、交通、工业和物流的集中地，也是高耗能、高碳排放的集中地。所以建设用地是各类土地中的主要碳源[30]，研究建设用地碳排放有利于实现建设用地的集约利用与科学管控。基于此，本文拟通过库兹涅兹曲线模型对1995年到2015年间全国30个省级行政单位的建设用地碳排放与灯光指数的关系进行实证分析，验证灯光指数与建设用地碳排放量之间是否存在库兹涅兹曲线关系，不仅有利于厘清碳排放与夜间灯光之间的内在关系，更有利于促进建设用地的集约节约利用。

1 研究数据与处理

1.1 灯光指数计算

本文选用的夜间灯光数据为1995—2012年度DMSP/OLS与2012—2015年月度NPP-VIIRS数据，来源于NOAA/NGDC网站。首先，根据曹子阳等[31]的方法处理DMSP/OLS数据，对数据进行裁剪、重投影、重采样、相对辐射校正与连续性校正最终得到1995—2012年之间的中国区域的夜间灯光数据；针对NPP-VIIRS数据存在负值、极高值、不稳定光源以及缺乏可比性与年值数据的缺点，本文利用2012年的DMSP/OLS数据替换NPP-VIIRS月度数据中的负值再求出2012年度NPP-VIIRS均值图像，剩余NPP-VIIRS数据中的负值则由前一年的年度均值图像替换并求出消除负值后该年度的均值图像，之后，利用不变目标区域法进行相对辐射校正，保证各年数据之间的可比性；利用低通滤波消除极高值；最后将各年度均值图像转化为二值图，在图中有光源的地方赋值为1，否则为0，根据不稳定光源不可能同时存在于前后两年间的同一地方这一假设，视前后两年中都等于1的区域为稳定光源区域，消除数据中的不稳定光源。最终，得到1995—2015年的中国区域夜间灯光数据。再根据公式1计算出平均灯光强度ANLI(average night light index，ANLI)作为灯光指数。但是，由于两代夜间灯光数据的分辨率与传感器不同，因此本文采取线性调整的方法(公式2)，即根据两代灯光产品在同一省份、同一时间点(2012年)内的平均灯光强度比例关系对NPP-VIIRS与DMSP/OLS的ANLI指数进行统一。

(1)

式中：ANLI为平均灯光指数；DNi为区域内第i级的灯光亮度；ni为区域内第i级的灯光亮度的像元总数；N为区域内所有的亮值像元总数;Nmax为最大灯光亮度。

(2)

式中：(ANLIcorr)i，t表示经过统一后的i地t年NPP-VIIRS数据的平均灯光强度；ANLIdmsp2012表示2012年DMSP/OLS数据的平均灯光强度总值；ANLIviirs2012表示2012年NPP-VIIRS数据的平均灯光强度总值；(ANLIviirs)i，t表示校正前i地t年的NPP-VIIRS数据的平均灯光强度。由于夜间灯光数据构建的灯光指数可作为城市化水平强度的衡量指标[32]，因此，文中关于灯光指数与建设用地碳排放的分析均从城市化的角度进行。

1.2 建设用地碳排放量测算

本文利用间接估算法测算建设用地碳排放量，用生产生活中能源消耗产生的CO2量来代替建设用地的碳排放量(表1)，根据IPCC提供的方法(式(5))测算出1995年到2015年间全国30个省、直辖市(不包括西藏、澳门、香港与台湾)的建设用地碳排放量，由于行政区划的调整，本文中1997年后的重庆市碳排放量并入四川省。

(3)

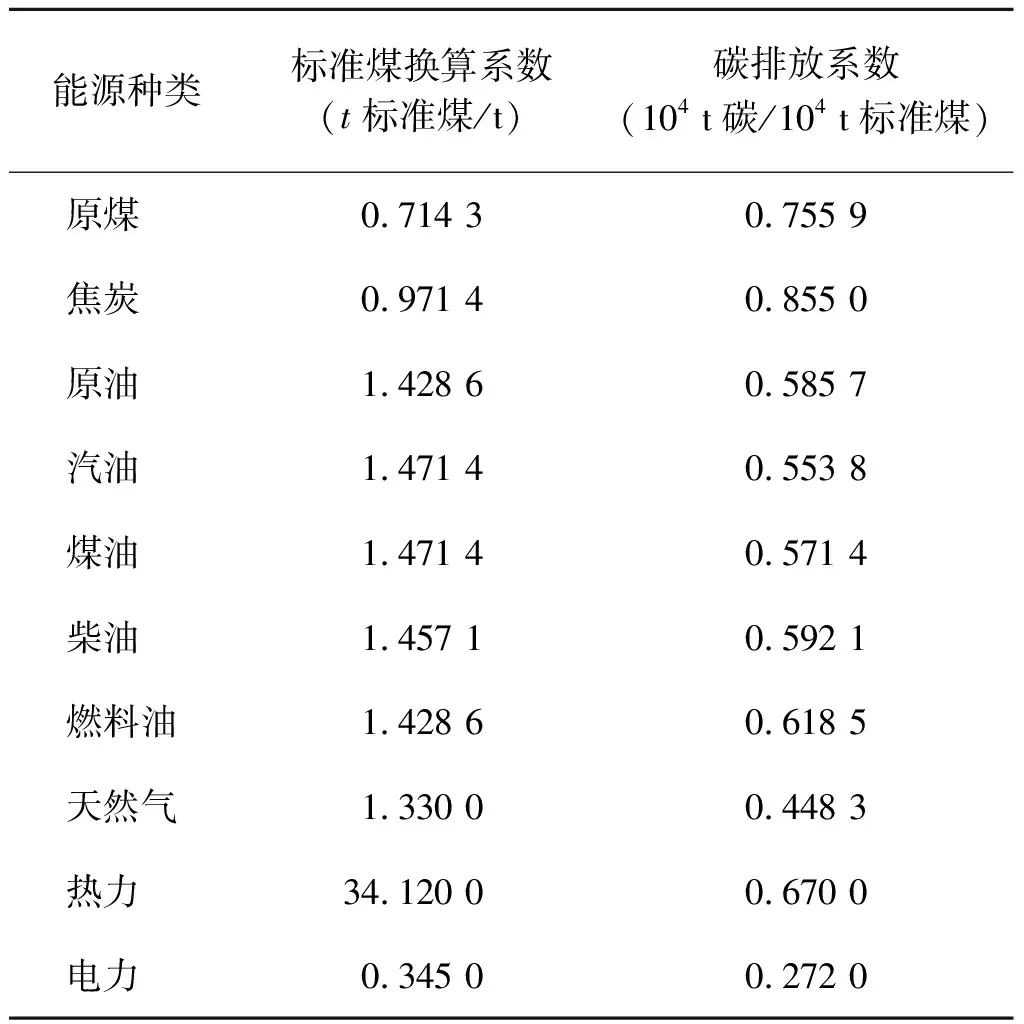
表1 碳排放测算系数表

2 模型构建与检验

当前文献中研究EKC模型主要是利用二次函数或者三次函数进行拟合，不同函数拟合出的曲线形态不同，利用二次函数拟合出的曲线多为倒U型或U型[33-38]。利用三次函数拟合出的曲线多为倒N型或N型[39-41]。但在中国三次函数模型所得的2个Turning Points 无经济意义[42]，因此，本文利用二次函数构建库兹涅兹曲线模型，为了减少异方差的影响，本文对自变量与因变量分别取对数，最终构建出如下模型：

lnCCEit=α+β1，ilnANLIit+β2，i(lnANLIit)2+εit

(4)

式中：lnCCE为建设用地碳排放总量；lnANLIit为灯光指数；α、β为待估计的系数；εit为随机误差项。当β2=0时为直线；当β2<0时为倒U型曲线；当β2>0时为U型曲线。

3 库兹涅兹曲线实证

3.1 单位根检验

一些非平稳的经济时间序列能表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R2，但其结果是没有任何实际意义。为了避免伪回归现象的出现，就要进行单位根检验确定数据是否为平稳数据。本文利用ADF与PP检验对数据进行单位根检验(表2)。通过表3可以发现利用原数据进行单位根检验时，无论是ADF检验还是PP检验中，P值都等于1，说明数据存在单位根为非平稳数据。对数据进行一阶差分后再进行单位根检验，发现在含常数项、含常数项与趋势项以及不含常数项与趋势项3种形式中，所有变量的P值都在0.05水平上显著，通过了ADF检验与PP检验，证明lnCCE、lnANLI与(lnANLI)2都是一阶单整数据。同样地，东中西部的所有变量也为一阶单整数据，但限于篇幅，本文只列出全国检验的结果。

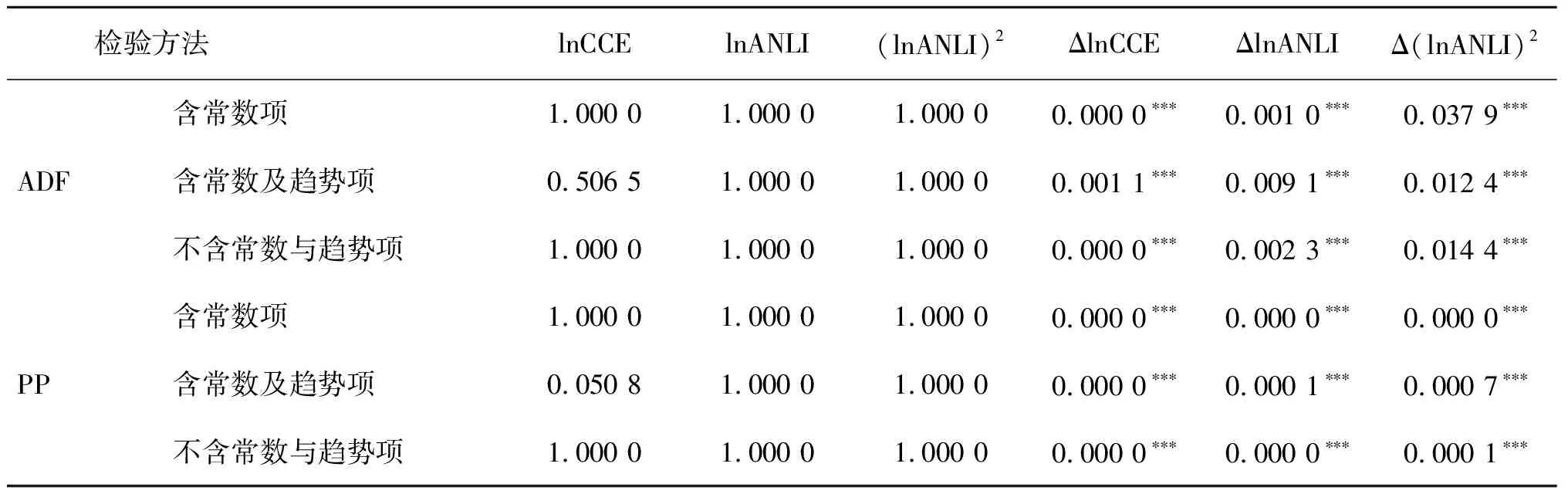
表2 全国单位根检验结果表

3.2 协整检验

由于灯光指数与建设用地碳排放量为非平稳数据，不能直接进行回归，需要通过协整检验判断ANLI指数与建设用地碳排放量之间是否存在长期稳定的关系。本文首先根据SIC与AC的信息量判断协整检验的最佳滞后阶数为4，再利用Kao检验对数据进行协整检验，结果如表3。发现在全国以及东中西部KAO检验的P值都在0.05的水平上显著，说明lnCCE、lnANLI与(lnANLI)2之间存在长期稳定的关系。

表3 协整检验结果表

3.3 格兰杰因果检验

lnANLI与lnCCE之间存在长期稳定的关系，但是，关系的方向性并不清楚，为了明确二者关系的方向性，本文取滞后阶数2、3、4分别对lnANLI与lnCCE做格兰杰因果检验，得到表4。发现在全国以及西部lnANLI与lnCCE既存在双向因果关系也存在lnANLI对lnCCE的单向影响关系，而在东中部只存在lnANLI对lnCCE的单向影响，综合考虑，本文认为在全国以及西部lnANLI与lnCCE为双向因果关系，而在东中部lnANLI与lnCCE为单向因果关系且是lnANLI对lnCCE具有影响。

表4 格兰杰检验结果表

3.4 模型选择与回归

格兰杰因果检验表明，无论是在全国还是在东中西部至少可以保证城市化是建设用地碳排放的Granger原因，因此，可以进行回归分析。回归之前本文利用F检验与Hausman检验确定不同区域中最合适的回归方式(表5)，最后利用构建的二次EKC模型进行回归，得到表6，通过表6发现回归后的调整R2都在0.75以上，最高达到0.92，F值也较大，除了西部区域的β2参数不显著外，其余都比较显著，说明模型回归的结果较为可靠。

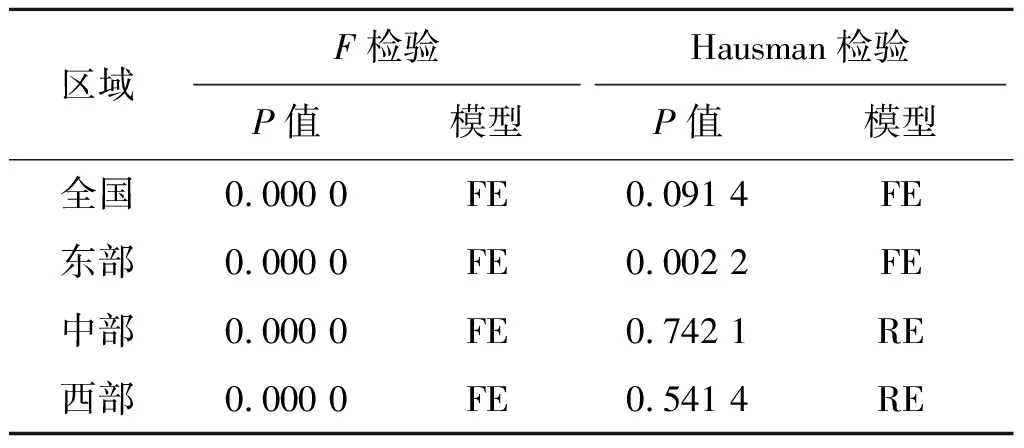
表5 模型选择结果表

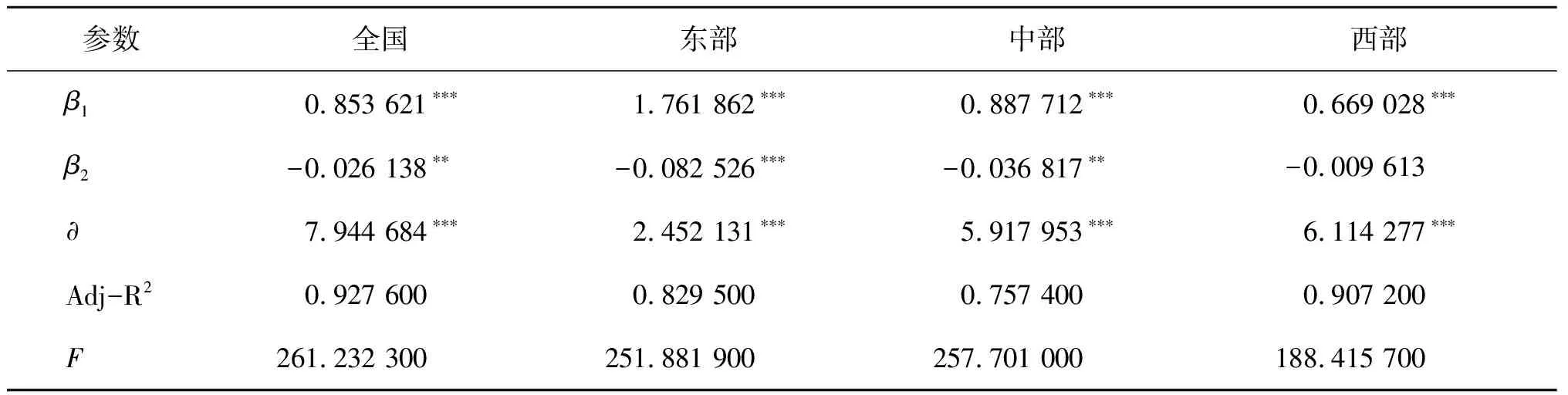
表6 模型回归结果表

4 结果与分析

通过协整检验与格兰杰因果检验发现，ANLI指数与建设用地碳排放量存在着长期稳定的关系，且在全国与西部二者为双向因果关系，说明在全国以及西部城市化会促进建设用地碳排放量的增长，建设用地碳排放量的累积也会促进城市化水平提高[43]；而在东中部为城市化对建设用地碳排放的单向因果关系，意味着在东中部城市化的提高会导致建设用地碳排放量的增长，但并不依赖碳排放的累积。这反映了全国以及西部的城市化水平提高方式较为粗放，其整体的城市化质量低于东中部。

通过回归结果发现，无论是在全国还是东中西部，β1都大于0，β2都小于0，证明了ANLI指数与建设用地碳排放存在着倒U型的曲线关系，也意味着城市化与建设用地碳排放存在倒U型的曲线的关系。因此，在建设用地碳排放拐点到来之前，随着城市化的推进，需要大量建设用地与能源，在这个阶段建设用地碳排放的总量会随着城市化进程的加深而不断增加，此时城市化对建设用地碳排放起着驱动作用。当拐点到来后，尽管社会的发展仍然离不开建设用地的扩张与能源的消耗，但当城市化发展到一定程度时，高耗能的发展模式不可持续，为了保护生态环境、实现绿色发展与低碳发展，倒逼社会不断改善能源消费结构、发展新型能源、提高建设用地的集约节约利用程度，此时，建设用地碳排放的总量也许会依然增加，但是增长的速度与强度会受到城市化的作用而减缓，此时城市化对建设用地碳排放起着抑制作用。

通过表6发现，在其他条件不变的情况下，全国以及东中西部的ANLI指数每增加1单位，建设用地碳排放量会大约增加0.85、1.76、0.88、0.66单位。证明城市化对建设用地碳排放的贡献会随区域变化，其中东部最高、西部最低，中部与全国位于二者之间。为探究造成城市化对碳排放区域差异的原因，本文利用夜间灯光数据与邻域分析法[44]提取了1995年到2015年的全国各省的建设用地面积(Kappa系数达到0.85以上)，并从统计年鉴中获得各省的人口与GDP数据，发现各省的建设用地面积、人口与GDP都呈现出东部>中部>西部的特点(图1～图3)。也即东部的城市化水平每提升1%，会带来比中西部更多的建设用地、人口与GDP，产生更多的碳排放量。同理中部的城市化水平每提升1%所产生的建设用地碳排放量高于西部，而在全国尺度上城市化所带来的建设用地碳排量放则位于东西部之间，略低于中部，也即相较于全国整体水平与西部，东中部拥有更高集约程度的城市化水平。因此，城市化对建设用地碳排放按贡献大小可排列为东部>中部>全国>西部。

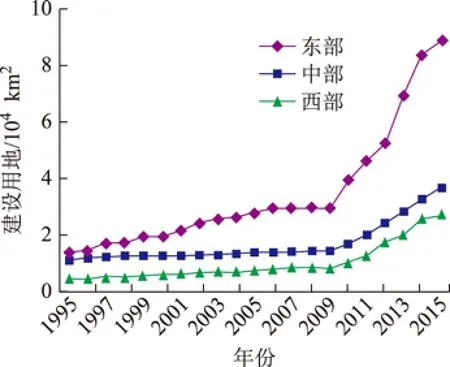
图1 1995—2015中国东中西部建设用地变化趋势

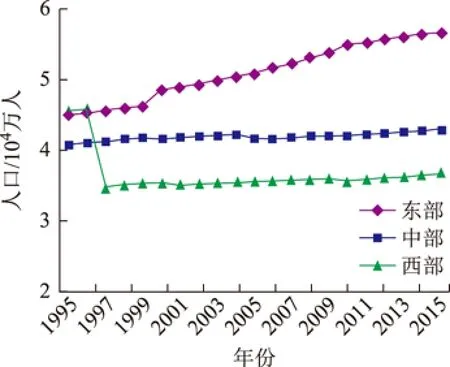
图2 1995—2015中国东中西部人口变化趋势图

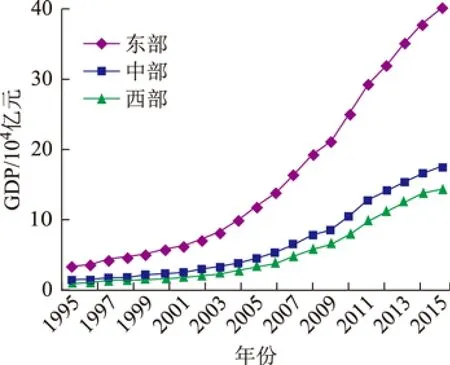
图3 1995—2015中国东中西部GDP变化趋势图

5 结束语

本文通过二次EKC模型与静态面板回归证实了中国区域内夜间灯光与建设用地存在着倒U型曲线的关系，发现了在东中部建设用地碳排放的累积并不是城市化的Granger原因，说明东中部的城市化并不依赖于建设用地碳排放的增长，逐步实现了城市的绿色发展，但从全国以及西部地区来说，城市化的提高仍然依赖于建设用地碳排放的累积。反映了东中部的城市化质量高于全国整体与西部地区的城市化质量，而总地来说我国的城市化发展模式还属于要素驱动，因此，未来需要进一步推动经济转型升级，促使城市化由要素驱动向创新驱动发展的转变，早日实现低碳发展。另外，本文证实了夜间灯光与建设用地碳排放之间存在倒U型的曲线关系，说明随着城市化水平的提高会逐步实现建设用地碳排放强度的降低，然而，这并不意味着建设用地碳排放拐点会自行到来，因此需要政府与公众的共同努力，加快建设用地摊牌拐点的到来。最后，回归结果表明城市化对建设用地碳排放量的贡献具有区域差异性，其中，东部>中部>全国>西部，造成东中部贡献较大的原因是东中部具有更加集约的城市化水平，因此，目前我国不仅需要加快转变经济发展模式，还需要因地制宜地制定减排政策与城市化发展政策，积极构建资源节约型与环境友好型社会。

本文利用EKC曲线模型证实了夜间灯光与建设用地碳排放之间的内在关系，为利用夜间灯光数据估算碳排放提供了一定的理论支持，同时基于遥感数据来探析建设用地与城市化内在关系，相较于以往研究更加客观真实，有一定的理论意义。但是，本文所得结论是基于中国近20年的经济背景下所进行的实证，其他地区或许并不存在倒U型曲线的关系。另外，本文从城市化的视角初步探讨了在中国夜间灯光与建设用地碳排放之间存在着库兹涅兹曲线关系，但如何从城市化的角度深入分析夜间灯光与建设用地碳排放相互影响的内在机理与影响因素是将来需要补充与完善的问题。最后，本文虽然提出了线性调整的方法对DMSP/OLS数据与NPP-VIIRS数据进行统一，但随着时间推移，两代灯光数据的差异会越来越大，因此，该方法只适用于短时间内的调整，而如何获得长时间序列且具有可比性的夜间灯光数据，仍然值得进一步研究。