曲率约束的激光点云全局优化配准算法

马伟丽，2，王健，孙文潇

(1.山东科技大学，山东 青岛 266590；2.山东省水利勘测设计院，济南 250101)

0 引言

在物体表面三维重构[1]中，点云数据配准是最为重要的步骤。使用三维激光扫描技术[2-3]，可以得到被测物体表面点云数据，通过在多个视角下测量的点云数据，然后对多测站数据进行配准，最终获得完整的三维物体模型。点云数据配准精度，对三维物体模型重构和应用有着直接的影响。

目前，国内外提出了很多数据配准的算法，其中使用最为广泛的算法就是1992年Besl等[4]提出的迭代最近点算法(ite-rative closest point，ICP)以及它的改进算法[5-6]。为了使数据配准的结果更加准确，ICP算法使用时必须要满足2个条件：点云之间存在包含关系、点云之间初始位置不可以相差过大。数据配准常用方法有：特征点提取法[7-10]，根据曲率特征、法向量等信息提取特征点，由得到的特征点对完成配准；质心重合法[11]，计算点集的质心，并将2个点集作相对于质心的平移；标志点法[12-13]，人工粘贴标志点，通过标志点配准。上述配准方法，对点云间位姿和噪声程度有严格要求，同时容易陷入局部最优。

针对上述点云数据在配准中存在的问题，本文采用散乱点云建立的曲率信息研究点云的配准方法，在基于曲率特征配准的基础上，引入现在比较成熟的模拟退火法(simulated annealing，SAA)对点云数据拼接误差的参数进行寻优，避免局部最优。因此提出基于随机抽样一致性算法(random sampling consensus，RANSAC)提取曲率特征点，然后用距离最近原则寻找对应点对，最后使用模拟退火法防止陷入局部最优完成最终配准。

1 经典ICP算法

经典ICP算法[14]利用最小二乘最优匹配原理，通过迭代进行点云之间的刚体变换。首先已知两块待配准的重叠点云M和N，其中M为待配准点云，N为参考点云。M点集中的每一点Mi以最小距离原则在N中寻找对应点，对应点构成新的点集。所有对应点对的拼接误差[15]

(1)

式中：Mi为目标点集；Ni为待配准点集；n为匹配点对总数；λ、R、T分别表示点集M与点集N之间刚体变换的缩放参数、旋转参数、平移参数。反复迭代求出满足式(1)且收敛于给定阈值的转换参数，即为ICP算法配准的最终目的。ICP算法过程描述如下：

①寻找对应点对M’、N’；

②计算配准转换参数λ、R、T；

③修正待配准点云M得到新的点云M’；

④计算相邻两次迭代点集的距离差值di，点对匹配均方差收敛于阈值τ，即di-di+1<τ，则停止迭代，否则令i=i+1，并返回步骤①。

2 改进ICP算法

2.1 曲率特征点集的提取

数据配准时，对于待配准点云M和基准点云N，如果对所有点云进行匹配点的搜索，会非常繁琐且浪费时间，同时因为噪声的存在也会对特征点的选取产生影响。本文在进行曲面拟合局部点云时，加入RANSAC算法，以消除噪点的影响，最后利用曲率极值法来提取曲率特征点。

在三维欧几里得空间中，几何体结构的特征主要由曲率和法矢量来描述[16]。曲率是一种不随平移、旋转、缩放变化的特征，该特征可用高斯曲率KG、平均曲率KM、主曲率k进行描述，首先引入曲率度量公式[17]

(2)

(3)

式中：k1代表最大曲率；k2表示最小曲率；α代表度量曲率相似度。通过公式(2)、公式(3)度量曲率相似度，提取出具有相似结构的点云，然后配准2片点云。特征点提取的具体步骤描述如下：

①选任意一点为种子点，选取K领域计算包含的点个数，计算迭代次数L[18]由式(4)得出：

(4)

(5)

式中：A为点云数；a为拟合曲面方程所需最小点个数，在本文中a=6，P为a个点均为有效点的概率；ε是数据的错误率，表示局外点与总数据量之比。

②对点云任意一点，建立邻域点集合，设曲面方程[19]为

(6)

在K邻域内随机选取a个点，计算Qij的初始参数。

④重复步骤②～③，直到循环次数达L次，找到最大局内点，由参数曲面方程解出最优参数Qij。

(7)

(8)

⑥由求得的高斯曲率与平均曲率可直接求解主曲率

(9)

(10)

⑦判断该点主曲率k1或k2在对应的主方向上是否为极值，若为极值，则保留该点，进行下一个种子点判断。重复步骤⑦～⑧，直到遍历完所有的数据。

⑧曲率极值越大特征越明显。为曲率极值设定一个阈值ω，大于该设置阈值则保留曲率特征点，反之删除。选取曲率特征点集流程图如图1所示。

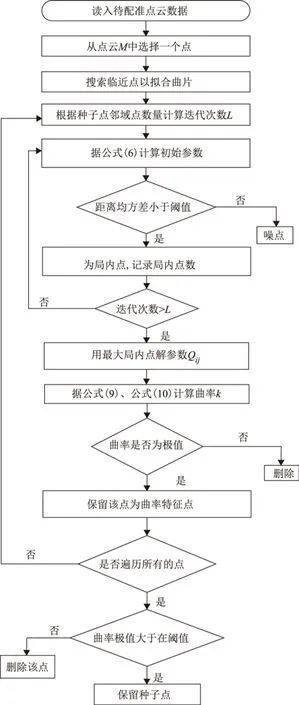
图1 选取曲率特征点集流程图

2.2 获取全局最优转换参数

配准的过程即是求解待配准点云到基准点云的缩放参数λ、刚性旋转R和平移T的过程。待配准点云M中的A点和基准点云N中的B点，表示的是地球表面物体的同一个点，可以通过缩放、旋转和平移变换把A点和B点重合在一起。A点坐标XA，YA，ZA，B点坐标XB，YB，ZB，转换的公式为：

(11)

在实际测量中，点云的采集不可避免带入噪声，虽然根据曲率特征选取特征点，以距离最近为判断依据获得相对应的特征点对，但是点云间数据没有绝对的一一对应关系，因此引入模拟退火法，得到使目标函数最小的最优转换参数λ、R、T，避免配准时出现局部最优解。目标函数的形式多样化，本文使用拼接误差公式(1)作为目标函数。

在1953年，Metropolis[20]等率先提出了模拟退火法。模拟退火法是一种非线性反演，能够避免使反演陷入局部极大值，是一个不断寻优的过程。在此过程中，拟合度随迭代次数的增加呈现一种跳跃起伏的现象，但总体的趋势是变小或变大，然而正是由于模拟退火允许拟合误差变大或拟合度变小，进而使得模型从局部的最优值中跳出来，最终得到全局的最优化模型。因此引入模拟退火法，在点云拼接过程中以拼接误差Eλ，R，T为目标函数，进行优化求解。

在模拟退火法的迭代过程中，要求温度随着迭代次数的增加而缓慢降低，由冷却进度表控制温度t的逐步下降，同时依概率接受恶化解。接受概率参数是关于温度t的函数，随着t不断的降低，接受概率也不断降低，直到最后不再接受任何恶化解。本文采用双曲下降型[21]退火方案。模拟退火法寻找转换参数的最优具体解步骤：

①初始化目标函数模型参数λ0、R0、T0，确定参数变化范围，选择初始温度t0=1°。

②计算目标函数值E0λ0，R0，T0。

③对当前模型参数进行扰动，产生新的模型参数λ1、R1、T1。

④计算新模型参数下的目标函数值E1(λ1，R1，T1)。

⑤计算目标函数差ΔE，ΔE=E1-E0。

⑥判断新模型参数是否接受，依Metropolis准则[22]为判断依据：若ΔE<0则接受；若ΔE>0，则新模型参数以概率P进行接受。

P=exp-ΔE′/t

(12)

式中：t为温度。

⑦接受新的模型参数时，设置λ0=λ1，R0=R1，T0=T1。

⑧在温度t下重复一定次数的扰动接受。

⑨降温t

tG=t0αG1/a

(13)

式中：t0为初始温度；G为迭代次数；α为给定常数，本文α=1。

⑩重复步骤③至⑨，直到收敛条件满足。

2.3 改进ICP算法流程

改进配准点云的ICP算法步骤如下：

①读取需要配准的2个点云：待配准点云M，基准点云N。

②利用RANSAC算法的二次曲面法对其K邻域进行曲面拟合。

③根据结合式(9)、公式(10)计算该点主曲率k1、k2，并判断是否为曲率极值点，遍历所有点云数据，并删除小于阈值μ的曲率特征点，得到基准点集M’。

④根据②、③计算待配准点云数据的曲率特征点，得到待配准点集N’。

⑤令为M’0、N’0迭代运算初始点集

⑥以距离最近为依据，查询特征点对(M’0、N’0)。

⑦根据步骤⑥获得的对应点集使用四元数法计算，获取缩放参数λ、旋转参数R、平移参数T。

⑧使用步骤⑥获得的λ、R、T对点云M利用公式(11)进行变换，得到新的点云。

⑨依模拟退火法判断是否为全局最优，既公式(1)全局最小，是则保留，否则重复⑤至⑧直到拼接误差为全局最优，最终完成配准，算法流程图如图2所示。

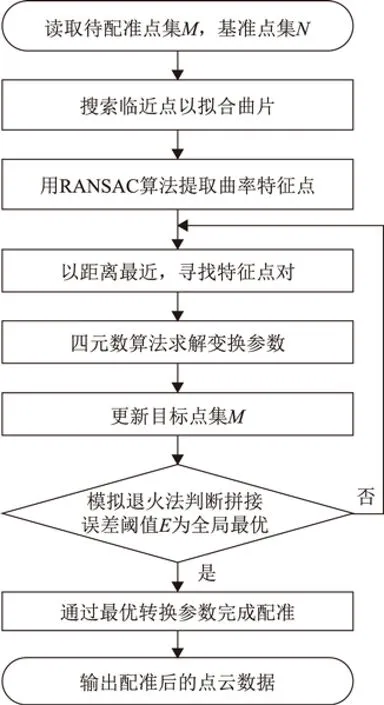
图2 算法流程图

3 实验验证与结果分析

为了验证本文算法的正确性、有效性和实用性，进行以下2组实验。实验数据采用斯坦福大学的Horse点云模型和Trimble TX8扫描仪采集某教学楼点云数据进行数据配准实验。所选用的2组数据都有十多种点云视角数据，在每组数据中随机选取2种视角进行配准，并与经典ICP算法进行比较。本文算法是在经典ICP算法基础上进行的改进，算法中加入了噪声点的剔除和避免出现局部最优，使其相对于经典ICP算法针对部分重叠点云的配准问题得到较好的结果。实验在Matlab 2010b软件环境下编程实现。

3.1 实验一

图3 Horse点云配准结果

为验证本文方法的正确性，本文对所选用斯坦福大学的Horse点云数据进行配准，并将本文方法与经典ICP算法配准结果进行比较。图3为Horse点云配准结果图，红色点云为基准数据，绿色点云为待配准数据，其中图3(b)为经典ICP算法配准结果，图3(c)为本文所提改进算法配准结果。

从图3可以直观地看出采用经典ICP算法配准结果较差，两站点云不能很好地贴合在一起，虽然两站点云有一部分可以配准在一起，但是仍有大量点云数据配准失败；而本文所提算法配准结果较好，经计算对应特征点对距离中误差为2.7×10-3mm。虽然本文所提算法会增加配准时间，但配准结果可以体现出本文所改进的算法可以很好地克服经典ICP算法容易陷入局部最优解的情况。

3.2 实验二

为验证本文算法的通用性和实用性，选取Trimble TX8扫描仪采集某教学楼的点云数据为实例进行验证。所选用的某教学楼点云数据有十多站点云视角，在实验数据中随机选取两站数据进行配准，并与经典ICP算法进行比较。图4为两站点云配准前后对比图，红色点云为待配准点云M，绿色点云为基准点云N。未配准的两站数据如图4(a)所示，用本文算法配准后点云数据如图4(b)所示。

图4 整体点云配准前后对比图

本文为验证该方法的稳定性和避免局部最优，采用2种算法对某教学楼的2个不同视角的点云进行配准。图5为2种算法局部配准结果图，其中图5(a)为ICP经典算法的精确配准图，图5(b)为为本文算法的精确配准图。

图5 2种方法局部配准结果

从图5可以直观地看出利用经典ICP算法配准后，待配准数据和基准点云数据之间有倾斜、错层现象。本文所提算法使两站点云数据相互重合优于经典ICP算法。因此，利用本文算法可以更为精准地进行配准，同时稳健性更强。

为定量描述本文方法的配准效果，在配准后的点云数据中选取房屋角点作为特征点，计算配准后对应角点的距离，绘制距离误差图，如图6所示。在获取到的点云数据中，很难找到2个对应的点数据表示真实物体的角点，本文利用平面拟合获取待评价角点周围的3个平面信息，进而通过3个面相交得到角点坐标。

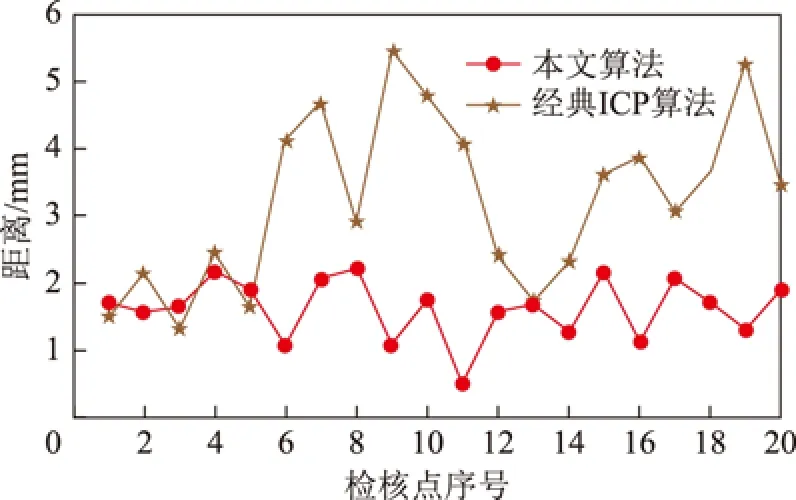
图6 配准后对应角点距离残差

从图6可以清晰看出利用经典ICP算法配准后，大部分检核点的配准误差在2 mm左右，但有部分检核点配准误差大于5 mm，这是由于通过经典ICP算法进行配准，出现局部最优情况而产生影响。本文算法在提取的特征点时加入结合RANSAC算法，从而去除噪声的影响提取特征点，同时利用模拟退火算法得到最优的转换参数，使配准误差优于2.5 mm，且误差分布较均匀。实验配准图和实验获得的对比数据，充分表明本文所提配准方法比经典ICP算法更稳定、精度更高。

4 结束语

在多视角测得散乱点云数据的情况下，利用经典的ICP算法得到的配准结果稳定性不高，容易陷入局部最优。针对这一问题，本文在经典ICP算法的基础上，引入了一种模拟退火算法寻找全局最优的配准方法。该方法的核心思想是结合RANSAC算法剔除粗差点从而达到稳健的效果，采用模拟退火算法避免点云配准陷入局部最优使得拼接误差最小，得到全局最优完成数据精确的配准。实验结果表明，本文数据配准算法提高了配准的稳定性和配准精度，能够满足多视角点云数据的配准要求，验证了本文提出算法的可行性。