基于DMSP/OLS数据的长江经济带城市用地空间分异特征

，3

(1.兰州交通大学 测绘与地理信息学院，兰州 730070；2.甘肃省地理国情监测工程实验室，兰州 730070；3.中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室，北京 100101；4.华北理工大学 矿业工程学院，河北 唐山 063009)

0 引言

按照诺瑟姆城市化发展规律曲线(S型曲线)，中国的城市化正处于发展的加速阶段(acceleration stage，城市化水平30%～70%)，发展速度和规模在人类历史上前所未有。1978—2016年人口城镇化率从17.92%增加到57.35%，城镇人口从1.72亿增至7.93亿元[1]，城市人口数量剧增，一方面促进城市化进程，加快人才的聚集；另一方面带来的诸如城市交通拥挤、环境污染等问题不断塑造和改变着城市空间结构与形态。长江经济带作为世界上人口最多、城市体系最为完整的流域经济带，同时也是推动中国区域发展格局由“T”字型战略转变为适应新常态下“H”型空间战略格局的重要支撑带[2]，其城镇化的健康发展对中国城镇化的整体发展起着至关重要的引领作用。因此，作为未来社会经济发展中最具活力和潜力的核心增长极点，如何及时准确地获取长江经济带城市扩张信息，对于优化城市空间布局、引导城市精明增长、评估城市可持续发展具有重要意义。城镇化的相关研究从数据源上可以分为两大类：基于统计数据的研究[3-4]和基于中高分辨率卫星遥感数据(Landsat TM/ETM+)的研究[5-6]，其中统计数据处理过程虽然相对简单，但缺乏足够的空间信息，难以满足城镇用地时空格局研究的需要，而Landsat TM/ETM+等中高分辨率遥感数据虽能较为准确地表达空间信息，但需要投入大量的时间和人力来提取一个大区域的城市信息，无法及时有效地研究城市的时空动态。夜间灯光遥感图像为大尺度的城镇化研究提供了一种新的数据手段，由于能直观的表达人类活动，受到国内外学者的广泛关注，其应用领域涉及到经济发展[7-8]、人口密度[9]、能源消费[10]、城市发展[11-12]等各个方面。然而从目前有关的研究来看，尚无法支撑起不断增长的现实需求。当前，针对城市的研究在内容上多集中于城市空间扩展研究，如卓莉等[13]基于夜间灯光强度的时间变化特征对城市用地空间扩展类型进行分类；王利伟等[14]基于夜间灯光数据对城市空间扩张格局进行研究；Zhang等[15]分析了中国30个主要城市的城市扩张过程；在方法上多采用阈值法、突变检测法[16]、辅助数据比较法[17]；在研究区域上多为全国[18]或东部沿海发达地区及城市群，如Wang等[19]利用夜间灯光数据监测长三角城市群的演变；Su等[20]基于夜间灯光数据分析珠江三角城市群城市建成区的变化；Hu等[21]基于夜间光数据分析京津冀城市群的发展模式。

综上所述，基于DMSP/OLS的城市化研究逐渐成为研究热点，综合分析：一是现有的研究多集中在整个中国、东部沿海地区或重点城市扩展较多，鲜有针对流域尺度的研究；二是现有对城市的研究，缺乏对城市范围的识别，其提取的城市灯光数据多存在乡镇、农村聚落等干扰的现象。由于存在干扰灯光碎片的影响，城市的建成区范围就会被扩大而导致提取的城市面积误差率较高；三是现有研究多是从单一尺度对研究对象的扩张动态进行分析，而忽视了多尺度下城市空间的相互作用关系。在此背景下，本文以长江经济带为研究主体，运用可以有效剔除郊区灯光数据的支持向量机的机器学习方法，通过城市扩张强度、城市扩张方向和城市扩张形态进一步刻画多尺度下长江经济带城市扩展的时空特征。研究结果试图为流域城市化进程提供初步趋势判断，对流域城市协同发展具有一定科学参考价值。

1 数据来源与处理

研究数据来源主要包含3个方面：①DMSP/OLS夜间灯光数据，本研究采用美国国家地球物理数据中心(National Geophysical Data Center，NGDC)发布的第4版全球夜间灯光栅格数据作为基础数据(http：//www.ngdc.noaa.gov)，影像分辨率为1 km。夜间灯光数据的时间跨度较长，在采集过程中使用了6颗卫星收集数据，部分年份(1994，1997—2007)有2个卫星同时服役，共收集了34期影像，其中稳定灯光影像包括城市、乡镇的灯光及其他场所的持久光源且剔除了月光云及油气燃烧等偶然噪声的影响，有利于分析城市、城镇等的灯光。夜间灯光影像的DN(digital number)值取值范围为0～63。由于受卫星之间轨道参数、技术设备差异等的影响，不同传感器采集的数据不具有连续性和可比性，为了使噪声和差异最小化，需要对原始夜间灯光数据进行预处理。本文借鉴Liu等人[17]提供的二阶回归模型进行夜间稳定灯光数据的校准，以实验性的方式校准年度夜间灯光产品，以匹配F162006年的复合材料，并获得年度复合材料回归模型的系数。校准之后使用1992、1997、2002、2007与2012年的校正夜间灯光数据。最后，将夜间灯光图像重新投影到阿尔伯特等积投影中，重新采样到1 km。②基础地理信息数据，矢量地图数据主要来源于国家基础地理信息中心发布的1∶400万比例尺的国家、省级、市级的矢量行政界线。本文以研究区域矢量界线为掩膜对灯光数据进行提取，并利用分级出来的行政区划矢量数据，分尺度统计研究区间的城市建成区灯光亮度值，从而建立长江经济带时空数据属性库。③NDVI(normalized difference vegetation index)数据，本研究采用中国科学院计算机网络信息中心国际科学数据镜像网站发布的NDVI数据，选取MODIS (moderate-resolution imaging spectroradiometer)中国NDVI月合成产品中的每年的5—9月产品经过最大值合成(maximum value composites，MVC)生成所选年份的最大NDVI图像，然后结合预处理后的DMSP/OLS数据参与城镇信息的提取。

2 研究方法

2.1 支持向量机分类法

支持向量机分类法(support vector machine，SVM)是一种较新的基于统计学习理论的机器学习方法，在遥感影像分类研究中具有较强的优势。它以结构风险最小化为准则，选择最有利于分类器性能的分类样本在机器学习过程中有效的训练分类器，由于其优良的学习及分类性能，从而规避了传统基于夜间灯光数据提取城市建成区的阈值选取难题，且具有较高的提取精度。SVM起源于20世纪60年代Vapnik等人设计的最优超平面，在90年代并进一步结合Kernel学习法演变成非线性识别函数。最优超平面不但要求把类别准确分开，而且还要求分离间隔最大化。假设由两类别组成的大小为m的训练样本集。

A=xi，yi|x∈RN，y∈(±1)，i=1，2，…，m

(1)

对于线性情况，求解最优超平面的问题可以转换为如下二次规划问题，最优识别函为

(2)

式中：α为Lagrange算子；h为分类阈值。线性不可转化时，需要引入非负的松弛变量ξi(i=1，2，…，m)和错分惩罚因子C，求得的最优识别函数与上式相同。

对于非线性情况，需将原始特征向量通过非线性函数F(x)映射到高维线性特征空间，在该高维线性特征空间中构造最优超平面，并得到最优识别函数

(3)

本文采用Cao等提出的基于SVM的区域生长法[22]，通过结合NDVI确定城镇与非城镇样本，将选取的城镇和非城镇样本生成ROI(region of interest)文件，使用径向基核函数(radial basis function，RBF)对城镇与非城镇训练样本进行SVM算法分类，最后结合NDVI对分类后的图像进行判别，提取长江经济带城市建成区的信息。

2.2 扩张强度指数

为了便于比较不同研究时段内城市扩张的强弱，本文采用城市扩张强度指数(urban expansion intensity index，UEII)，表示不同时段城市扩张的空间分布，公式如下：

从波形图中也可通过对比得出在螺栓松动的情况下，由螺栓松动而引起的两联件之间的自由度增加，从而导致工件在振动时受到被联件的冲击作用，导致其振动波形呈现不规则性。是引起实验过程中相位差读数变化较大的主要原因。

(4)

式中：UEII表示时间跨度在t和t+i年之间空间范围城市建成区的扩张强度；UDNt+i和UDNt分别表示在t+i和t年城市建成区的面积；SDN表示空间范围内的总面积。通过考虑长江经济带上中下游不同区位的城市发展水平，计算UEII的3个空间尺度：整个长江经济带，长江经济带上中下游及核心城市。

2.3 标准差椭圆方法

标准差椭圆方法(standard deviational ellipse，SDE)能够精确地揭示地理要素空间分布的整体特征。SDE基于研究对象的空间位置和空间结构从全局性角度定量解释地理要素空间分布的中心性、方向性、展布性等特征，揭示地理要素的空间分布及时空演化过程。该方法被广泛地用于城市问题、经济空间格局等各个领域。标准差椭圆的参数主要包括椭圆重心、方位角、标准差椭圆长短轴，具体参数公式详见参考文献[23]。

3 结果与分析

3.1 流域城市用地扩张的空间分布特征

1)用地空间形态分布特征。1992、1997、2002、2007和2012年5个时段长江经济带的DMSP灯光空间分布图可以看出(图1)，以长江干流为轴线，形成明显的点-轴亮度空间特征，灯光密集区主要分布于下游长三角城市群、中游城市群与上游成渝城市群，其中，以上海为中心的长三角地区灯光亮度最高，最为集中，中西部省份灯光较明显的有武汉、长沙、成都、重庆、昆明等几大省会型城市。总体来说，长江经济带灯光分布与人口总量和密度空间耦合明显，从东部沿海向西部呈阶梯状减少。进一步通过SVM分类法将提取后的核心城市影像进行分析，长江上游地区的成都、重庆、昆明、贵阳多表现为主-副双核心的扩张模式，呈现明显的中心-外围格局，其中成都、重庆市的年均扩张速度最快，分别为40.63%、31.11%；长江中游地区的武汉、长沙、南昌均以主城区为中心快速发展，呈现典型的圈层扩展模式，虽然武汉市的年均扩张速度最小(12.87%)，但在1992—2012年的扩展中其建成区面积的总量始终保持着与长沙和南昌市总量之和对等的水平；长江下游地区的上海、南京、杭州、合肥均表现为多中心向外扩展，其年均扩张速度分别为10.43%、12.31%、42.08%和21.61%，年均扩张速度最小的上海市，因其土地面积有限和高基数，到2012年其建成区面积占上海市土地总面积的80%左右。

2)用地空间面积分异特征。研究采用SVM分类法从夜间灯光栅格数据中提取1992—2012年长江经济带城市建成区，并对不同尺度下研究区间内的建成区面积进行动态分析(表1)。研究发现长江经济带城市建成区在1992—2012年间保持持续增长，年均面积变化速度为31.41%，其城市建成区的面积从9 615 km2扩张到70 007 km2。从建成区面积变化的流域空间梯度差异上分析，1992年长江下游地区的建成区面积最大，其建成区面积约占长江流域总建成区面积的60.71%，中游次之，上游建成区面积最小。在1992—2012年的发展过程中，三大区域建成区面积都呈现不断升高的总体趋势，但不同区域建成区面积变化差异明显。上游和中游建成区面积都有相当稳定的扩大趋势，但增加幅度不同，上游的上升幅度明显高于中游，尤其到2002年之后，上游地区的总建成区面积超过中游并呈现强势上升的态势，下游地区的总建成区面积则不断上升且始终为三大区域面积总量最大。到2012年长江流域上中下游建成区面积年均增长速度分别为35.99%、17.34%和35.37%，达到了13 181 km2、9 694 km2和47 132 km2。

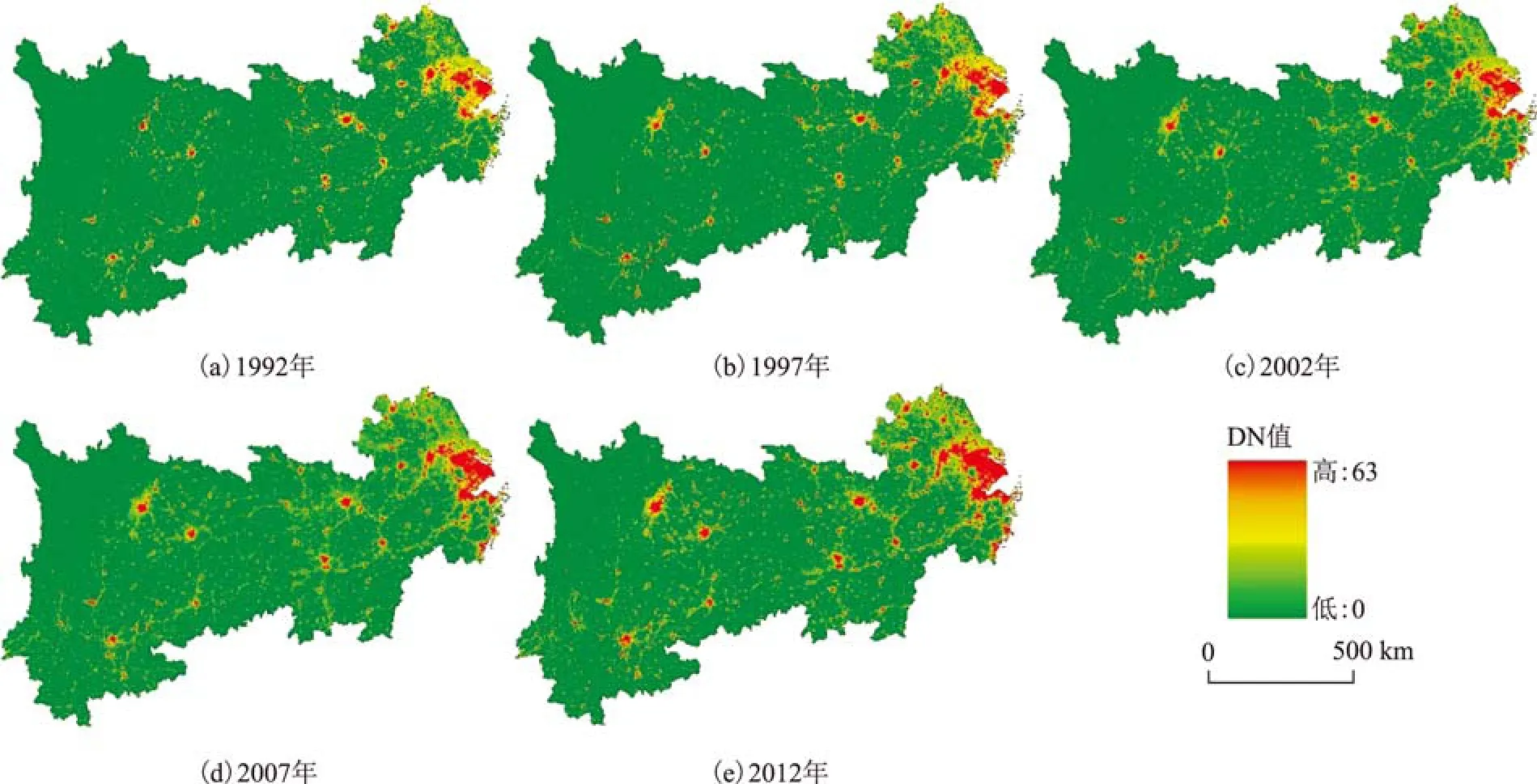
图1 长江经济带灯光空间分布变化图

表1 1992—2012年流域用地空间面积变化

3.2 流域城市用地扩张的时序演变特征

1)扩张强度时间演变特征。本文采用扩张强度指数计算3个空间尺度下的扩张强度，即长江经济带、上中下游地区和核心城市。首先从长江经济带及上中下游地区的城市扩张强度上可以发现(图2)：(1)长江经济带的扩张强度呈现“先升高-后降低-再升高”的趋势，1992—2002年长江经济带的城市扩张强度指数从0.08增加到0.15；2002—2007年出现小低谷下降到0.12；2007—2012年长江经济带的城市扩张达到高峰期，扩张强度指数达到0.35，是上一阶段的3倍左右，长江经济带城市迅速发展。(2)长江下游地区的城市扩张强度在1992—2012年均高于长江经济带扩张强度变化值，且在2007—2012年达到了最高值0.45；而长江上游及中游地区的城市扩张强度与长江经济带的走势是一致的且始终处于长江经济带扩张强度值之下。由于上中下游地区城市的区位条件、发展基础各不相同，其城市扩张随时间的扩张强度也各不相同，但总体上都在2007—2012年达到了峰值，分别为0.29、0.19、0.45。

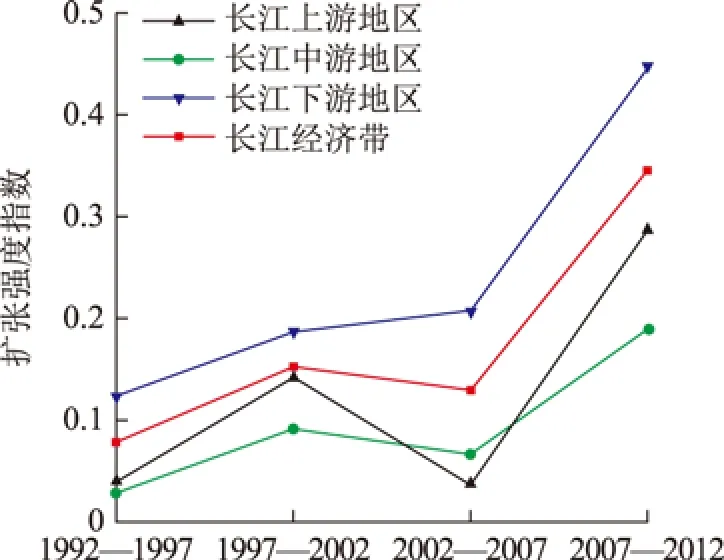
图2 经济带及上中下游地区城市扩张强度的变化

从长江流域上中下游核心城市扩张强度变化值来看(图3)，1992—1997年核心城市扩张强度在0.10之上的城市，上游地区只有昆明市，中游地区只有武汉市，而下游地区有3个，分别是上海市、南京市和杭州市，值得注意的是在1992—1997年上海市的城市扩张强度已远远超过其他城市的0.10左右，达到了0.60。2007—2012年城市扩张强度大于0.30的城市，上游地区除了昆明市之外还增加了成都和重庆两市且成都市的扩张强度达到0.63，成都市在此期间得到了迅速发展，中游地区也仅有武汉市，下游地区除上海、南京和杭州三市之外，合肥市也在其列。

图3 不同时期核心城市扩张强度的变化

从核心城市扩张强度的变化幅度来看，可以分为2种类型的变化走势，即“波动上升”和“波动下降”。其中“波动上升”是指研究期末比研究期初的扩张强度高，这种类型的城市数量居多，其中包含长江上游的所有城市、长江中游的所有城市和长江下游的南京、杭州和合肥。值得注意的是南京和合肥市的扩张强度呈现持续上升的走势，以南京市为例，其城市扩张强度从0.16持续上升到0.52。而“波动下降”是指研究期末比研究期初的扩张强度低，这种类型的城市数量较少，只有上海市，其城市扩展强度从0.60下降到0.47。虽然上海市的扩张强度在走低，但其扩张强度在长江流域所有城市中均处于较高水平。总体来看，不同区域城市扩张强度与其区域内关键节点城市扩张强度存在很大关联性。从上游地区来看，2002—2007年成都、昆明市的扩张强度变化值分别从0.38降低到0.16和从0.14降低到0.02，波动幅度均在2倍之上，上游地区的扩张强度受其影响在2002—2007年下降的幅度也较大。从中游地区来看，2007—2012年长沙、南昌市的扩张强度比2002—2007年的低，而武汉市的扩张强度则从0.19提高到0.43，中游地区的整体扩张强度也从0.06提高到0.19，表明武汉市对中游地区的影响较大。下游地区的城市扩张强度在20年间持续上升且始终处于长江经济带的变化曲线之上，结合上海市及其他区域内节点城市扩张强度值可知，这更多的受下游地区的长三角城市群所影响，以上海为核心的长三角城市群作为长江经济带的“龙头”将继续发挥显著作用。

2)扩张方向时间演变特征。本文通过标准差椭圆的面积变化大小和重心移动距离，分析长江经济带城市规模在空间上的集中程度和时间上的方向变化趋势(图4)。标准差椭圆的时空变化显示，1992—2012年长江经济带夜间灯光标准差椭圆分布范围由61.96 km2增大到76.52 km2，增长率为23.49%，椭圆短轴和长轴均呈现不同幅度的增长且长轴增长量较大，其重心经历了“东-西南-东北-西南”的变动过程(表2)，大致分为3个阶段：(1)1992—2002年长江经济带夜间灯光标准差椭圆分布范围由61.96 km2增大到75.63 km2，增长率为22.06%，空间上呈现扩张的趋势，其重心偏东南移动，移动距离28.68 km，这一时期属于市场经济发展初期，在对外开放政策的影响下，东部沿海地区发展迅速，推动长江经济带椭圆及重心向东南偏移。(2)2002—2007年，长江经济带夜间灯光标准差椭圆分布范围由75.63 km2缩减到69.11 km2，增长率为-8.62%，空间上呈收缩的趋势，其重心偏东北移动，移动距离54.38 km，这可能是由于2003年“非典”事件对实体经济造成严重的负面影响，导致资源为躲避危机而四处转移，空间分布零散而呈现收缩之势。(3)2007—2012年，这一阶段夜间灯光标准差椭圆分布范围由69.11 km2增大到76.52 km2，增长率为10.71%，空间上呈扩张趋势，且重心开始偏西南移动，移动距离43.22 km，在“西部大开发”和“中部崛起”利好政策以及中西部城市群战略的联动下，长江上中游地区的城市(成都、重庆、武汉等)发展速度加快，推动长江经济带重心偏西南移动。

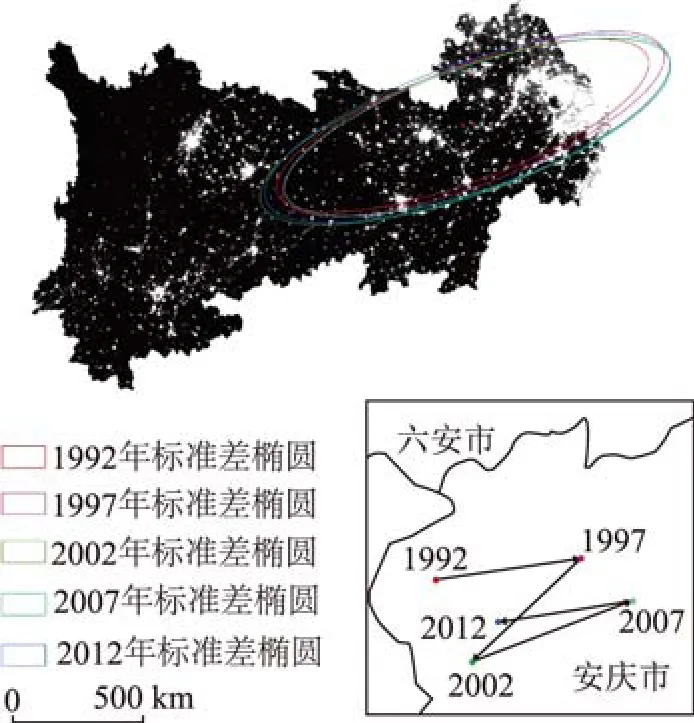
图4 1992—2012年长江经济带标准差椭圆及其重心变动

表2 长江经济带标准差椭圆变化

4 结束语

本文以长江经济带作为研究区，选取长时间序列的DMSP/OLS NTL图像来分析不同空间尺度下长江经济带城市的时空扩张。得到以下主要结论：

①长江经济带灯光的总体分布与人口相似，从东部沿海向西部呈阶梯状减少。不同区域的核心城市呈现不同的扩展模式，上游地区的城市多表现为 “主-副”双核心的扩展模式，中游地区呈现典型的圈层扩展模式，下游地区表现为多中心向外扩展。

②1992—2012年长江流域主要城市呈现快速扩张，建成区面积由1992年的9 615 km2扩张到2012年的70 007 km2，年均扩张速度为31.41%。流域的时空扩张以上海为龙头，呈现“上游-下游-中游”递减的扩张格局，3个区域扩张速度分别为35.99%，35.37%和17.34%。

③标准差椭圆分析表明长江流域城市总体灯光重心位于安徽省安庆市，且在1992—2012年期间呈现往复移动的现象。夜间灯光标准差椭圆分布范围由61.96 km2增大到76.52 km2，椭圆长轴增长幅度明显大于短轴增长幅度，具有明显的东西轴向性，重心坐标偏东南移动23.75 km，表明推动长江经济带城市空间演进的主要力量以东西方向的城市增长为主且下游的城市对其主导性较强。

④扩张强度分析表明长江流域城市扩张强度总体呈现波动上升趋势，2002—2007年长江经济带及上中游地区呈现下降趋势，核心城市扩张强度解析表明上游地区的成都、重庆、昆明市，中游地区的武汉市表现不同幅度的下降；下游地区扩张强度指数则从0.12持续上升到0.45，长三角城市群对其影响最大，以上海为核心的长三角城市群作为长江经济带的“龙头”将继续发挥显著作用。

科学识别城市的扩展信息，准确掌握其空间变化特征及规律，对于优化城市空间、评估城市可持续发展具有重要意义。SVM分类法不仅可以从大城市和小城镇的斑块中识别出城市的范围，而且可以有效地防止郊区的一些碎片被包含在城市中而提取出来，达到很好的提取效果。本文通过一系列数据处理方法校准NTL图像，并结合NDVI数据采用SVM分类法来提取1992—2012年经济带城市的扩展信息，成功用于分析经济带时空变化规律的研究。然而NTL图像中的DN值在城市化的初期阶段可以有效地表达相应地区的城市化发展水平，但随着时间的演进，通过DN值的变化来反映高度发达城市的发展水平是有一定难度的，未来采用更高精度的夜光图像是研究探索的重点。