领悟优化 化繁为简

○方艳霞

人教版小学数学四年级下册第一单元《四则运算》中涉及到这样一个例题：

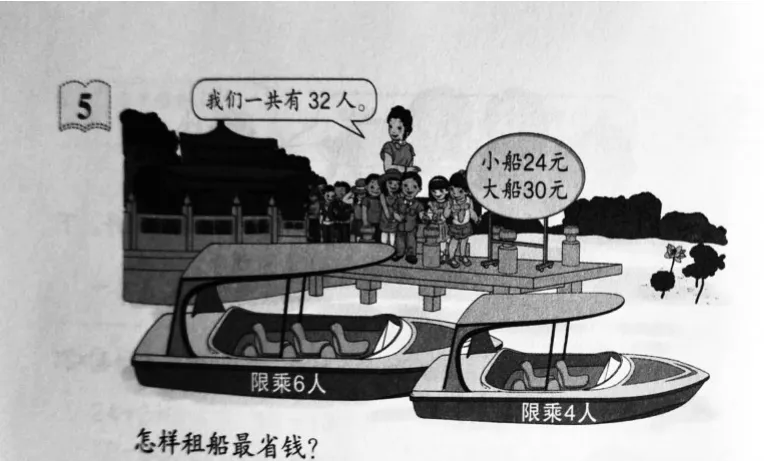
仔细观察情境图，请学生分析图上信息并用语言描述提炼出的相关信息。

师：想一想，我们在几年级的时候接触过类似的优化方案的题型？还记得我们是用什么方法解决的吗？

生：在三年级上册《测量》这一单元学习过这样的题型，我们是用列表法一一列举的。

师：好的，我们就用学过的方法来解决这个问题。

方案①②③④⑤⑥⑦大船6条5条4条3条2条1条0条小船0条1条2条4条5条7条8条租金180元174元168元186元180元198元192元

师：用列表法列举的好处就是可以很全面很有序地列出租船方案，不容易重复、遗漏，并能从中找到最优方案；但是这种方法也有缺点，就是题目中数目较大时，这样列举就很繁琐。

小组讨论：仔细观察这个表格，根据租金栏讨论一下，怎样租船相对便宜，看一看我们能不能找到一种简单的解决问题的方法？

学生在讨论的过程中会发现：只要所租船的座位数与租船的人数相等（也就是没有空余座位）时，租金就会比有空座位的便宜。

师：满足这个条件的有③⑤⑦三种方案，继续观察这三种方案中租金最便宜的还要满足什么条件？

生：租大船越多租金就越便宜。

师：这是为什么呢？

生：因为租大船单价便宜。

师：也就是说我们如果想找到最便宜的租船方案，就必须遵循两个原则：尽量坐单价便宜的船，租船人数与所租船的座位相等。根据以上原则，各小组试着想一想解决这个问题的步骤。

小组汇报解决问题的方法和思路：

第一步：大船的单价：30÷6=5（元）小船的单价：24÷4=6（元）

要先求出每条船的单价，这样就能知道租哪种船便宜了。

第二步：32÷6=5（条）……2（人）

5条大船1条小船 ：5×30+1×24=174（元）

因为租大船便宜，所以尽量让所有人坐大船，不过因为每条大船限乘6人，所以最后剩下的两个人只能再租一条小船了。

师：可是对照上面表格这也不是省钱的方案呀？

生：因为小船上有两个空余的座位，所以我们在尽量租大船的前提下，还要考虑怎么样做没有空余座位。（ ）×6+（ ）×4=32（人）

第三步：我们发现少租一条大船多租一条小船，租船人数和所租船座位正好相等。

4条大船2条小船：4×30+2×24=168（元）

好的数学教育应从学习者的生活经验和已有的知识背景出发，教师用已有的知识做铺垫，在教学中让学生自己弄清题意，理清已知信息数据和要解决的问题，把学习和思考的主动权交给学生，让学生有自主学习的时间和空间。学生在小组中充分交流自己的方案，借助集体的智慧对现实数据进行分析，在各种方案的比较分析中，最终发现最省钱的解决问题的方案，认识最佳方案选取的技巧以及该知识点在生活中的重要性。这样不仅使学生加深对最佳方案的理解并提高思考能力，而且让学生切实感受问题的现实性，充分感受到最佳方案的获取就在自己的身边。

《义务教育数学课程标准（2011年版）》强调：数学学习中，学生要全员参与。这里的参与并不是简单的行动上的参与，而是思维的参与。小组交流之前教师一定说明所要讨论的问题，这样学生不仅避免了合作学习流于形式，而且每个学生都围绕问题有自己的解决办法，在合作交流的基础上形成解决问题的步骤和方法，先求什么？再求什么？最后求什么？并且能够清楚每一步所求的题意。学生在交流中思维得到碰撞，在碰撞中提升数学思考力。这样的课学生明白的不只是一个知识点，而是一个整体，一个结构，一个思维方式。这也是我们一直追寻的简约而灵动的课堂。