基于误差空间的航天器姿态反步容错控制*
韩 宇,樊 炜,曹 涛
(1. 上海航天控制技术研究所·上海·201109;2.上海市空间智能控制技术重点实验室·上海·201109;3.上海卫星工程研究所·上海·201109)
0 引 言
姿态容错控制是指在航天器发生故障的情况下仍能保持航天器姿态稳定的控制方法,其对于在复杂环境下工作的航天器[1]而言具有重要意义,亦有众多学者在这一领域开展了研究。例如,文献[2]针对飞轮故障的情况,基于线性变参数系统设计了鲁棒容错控制方法;文献[3]设计了PID迭代学习容错控制律,可以解决连续时变的故障系统;文献[4]针对使用单框架控制力矩陀螺群的刚性航天器被动容错控制问题开展了研究,基于滑模控制理论解决了这一问题;文献[5]同样采用积分滑模的控制策略,解决了执行器故障的刚体航天器的姿态稳定问题;文献[6]对近年来的航天器姿态容错控制方法进行了总结,主要包括基于自适应理论的容错控制方法[7-11],基于滑模理论的容错控制方法[12-14],以及基于控制分配的容错控制方法[15-17]。目前而言,航天器的容错控制方法已具有针对外界干扰、参数不确定性、执行器故障等情况开展的分析及解决方案,但较少考虑了执行器安装误差等情况,且仍需进一步解决航天器在故障突发情况下的姿态快速回转机动能力,以及保持航天器高指向精度的问题。
Lyapunov方程一直是设计姿态控制律时判断系统稳定性的重要手段,而如何选取一个合适的Lyapunov函数一直是控制领域一个重要的讨论内容[18-19]。利用系统机械能的变化来定义Lyapunov函数,从而进一步得到全局稳定的控制律的方法,首先由Koditschek在文献[19]中提出。Lyapunov方程应包括系统的动能部分(与航天器角速度变化相关)及势能部分(与航天器姿态变化相关),其中势能部分可以基于误差空间的几何关系或刚体系统的能量损耗而求得。例如,文献[20]就是基于势能的最大值设计了全局稳定的反馈姿态控制律。文献[18]考虑了一种基于几何学的姿态控制方法,利用基于姿态四元数误差的二范数求得了系统势能的变化。然而,这两种方法都不是几何方法中最短路径的选择。本文通过误差空间拓扑所得的误差函数来描述势能误差,从几何层面上看,这是描述势能误差的最短路径选择。因此,在航天器发生故障的情况下,本文所提出的控制方法可以迅速调整增益,使得系统姿态误差迅速收敛至零,从而有效提高航天器在故障突发情况下的姿态快速回转机动能力。
1 航天器姿态动力学模型
1.1 姿态运动学与动力学模型
对于工作姿态为对地定向的三轴稳定航天器(假设其数学模型为刚体)而言,通常以轨道坐标系为参考坐标系,航天器的绝对角速度矢量ω∈R3。当取航天器质心C为参考点时,J为航天器转动惯量矩阵,则航天器的姿态动力学方程可表示为
(1)
式(1)中,τ∈Rn为所有执行机构产生的执行力矩,n为执行机构的个数,D∈R3×n为执行机构的安装矩阵,Td∈R3表示航天器所受外部干扰力矩。
以四元数来描述姿态,则航天器的姿态运动学方程可表述为
(2)
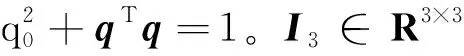
1.2 飞轮安装偏差模型
本文采用三正装一斜装的反作用飞轮组作为执行机构[21],执行机构的个数n=4,D∈R3×4。考虑到反作用飞轮制造与装配过程中机械精度、物理工艺技术的约束,发射过程中强冲击与振动,以及环境干扰力矩的影响,其安装构型往往与标称构型存在一定偏差,如图1所示。

(a)标称执行机构配置
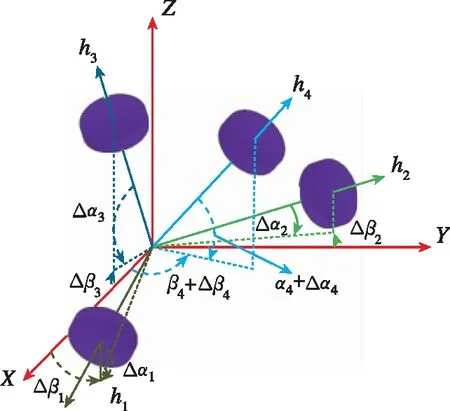
(b)存在安装偏差的执行机构配置图1 执行机构配置结构图Fig.1 Configuration of actuators in spacecraft
基于此,对执行机构安装偏差进行建模,则有如下形式
(3)
定义ΔD∈R3×4为安装矩阵的偏差或不确定性项。由于αi(i=1,2,3,4)、βi(i=1,2,3,4)均为小量,可以近似为cosαi≈1、cosβi≈1、sinαi≈αi及sinβi≈βi,则航天器执行机构的安装矩阵可写为
D=D0+ΔD
(4)
式(4)中,
(5)
ΔD=
(6)
1.3 飞轮故障模型
在卫星作业过程中,飞轮的消耗极大,其不仅需要长期运转,而且还会受到摩擦力矩和空间环境等众多因素的影响。常见的反作用飞轮故障有以下4种:①反作用力矩降低;②对控制信号无响应;③输出力矩叠加偏差;④反作用力矩不确定。根据以上4种故障形式,可以对反作用飞轮进行建模,单个飞轮的输出力矩可写为
(7)
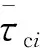
综上,根据飞轮安装偏差模型和飞轮故障模型,能够得出飞轮的实际输出力矩模型为
(8)
e3e4}表示4个飞轮的乘性故障。
1.4 问题描述
结合飞轮的安装偏差及故障模型,航天器姿态动力学方程可表示为
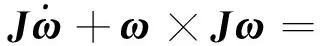

(9)
式(9)中,g(t)为航天器执行器实际力矩的乘性系数,后文用Tg表示;f(t)为航天器执行器实际力矩的加性偏差,后文用Tf表示。乘性系数矩阵可表示为
(10)
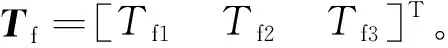
2 反步容错控制方法
2.1 航天器反步容错控制方法
由上文,航天器的系统动力学方程可简写为
(11)

(12)
(13)
式(12)和式(13)中,c1>0、c2>0均为给定正实数,H(q0)为与q0相关的函数,且满足
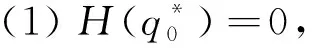

证明:控制器设计分为两步完成。
定义如下变量
z1=q
(14)
z2=ω-ua
(15)
式(15)中,ua为待设计的虚拟控制律,其定义将在后文给出。
第一步:选取与q0相关的Lyapunov函数
V1=2c1H(q0)
(16)
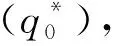
(17)
此时,选取相应的虚拟控制律ua为
(18)
则式(17)变为
(19)
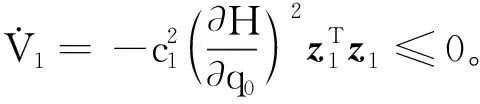
第二步,对于定义变量z2的微分,有
(20)
选取新的Lyapunov函数为
(21)
对V2求导有
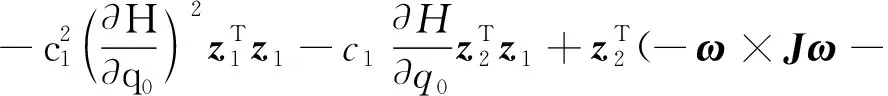
(22)
当考虑容错控制策略为
(23)
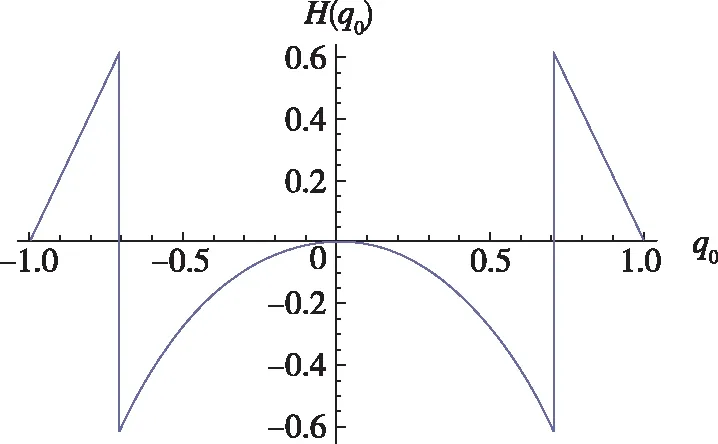
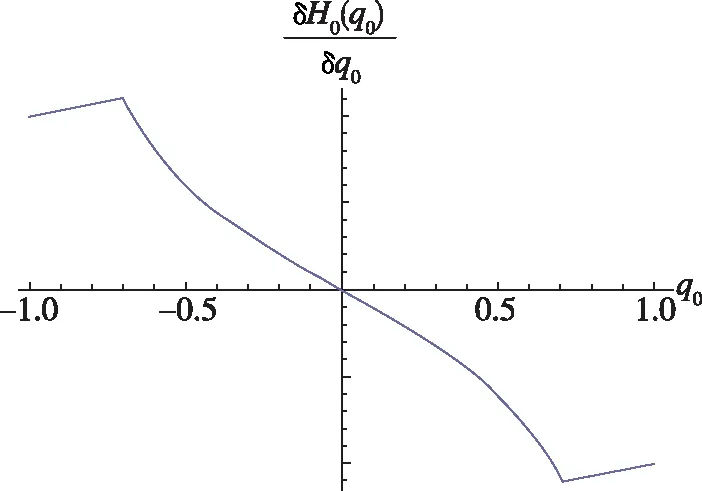
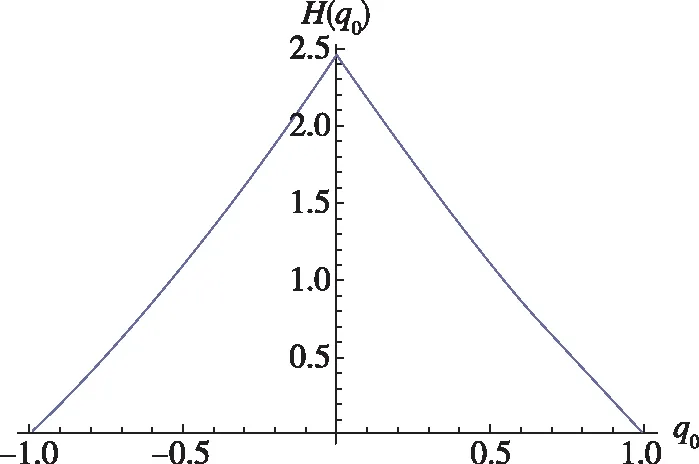
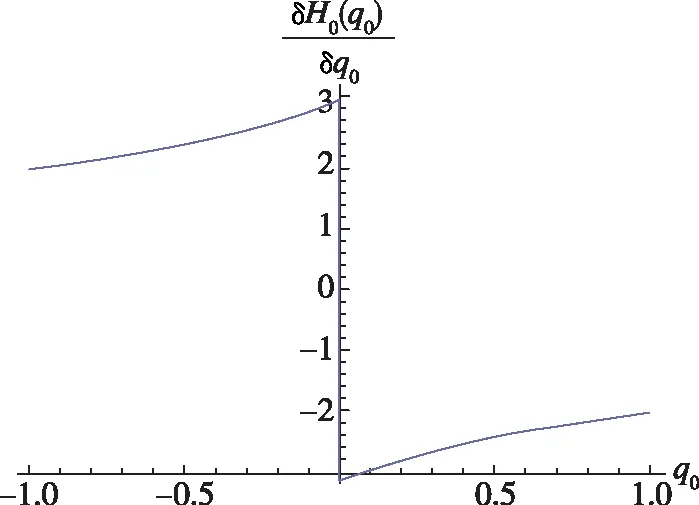
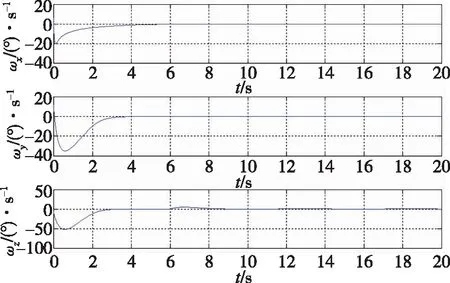
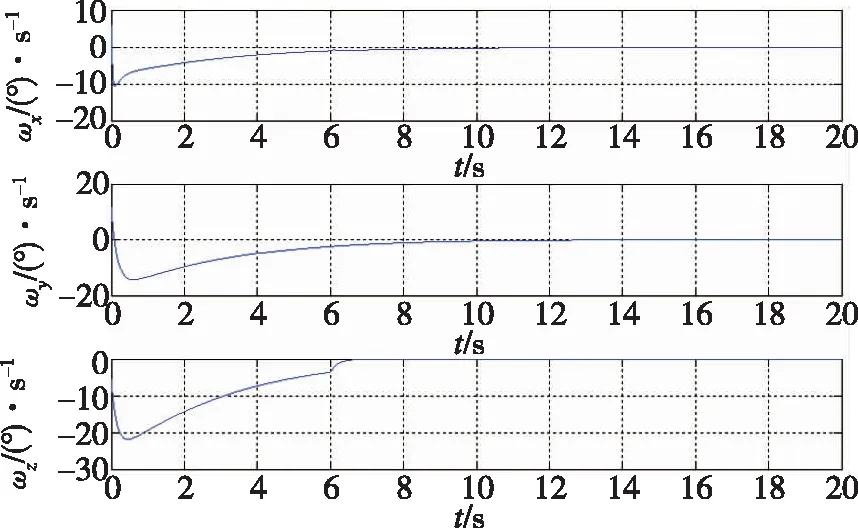
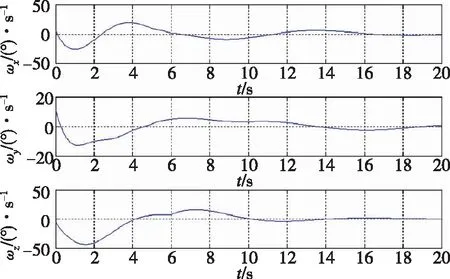
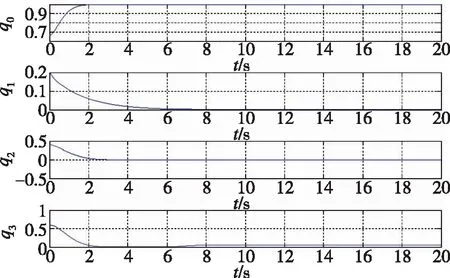
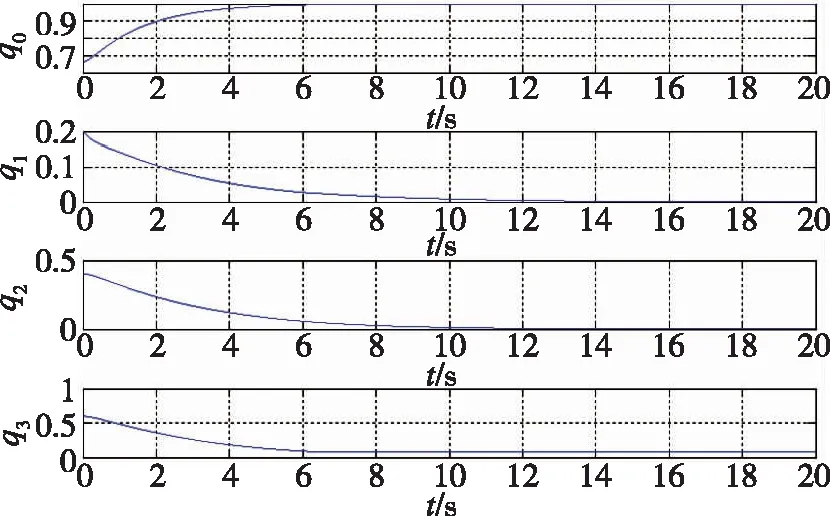
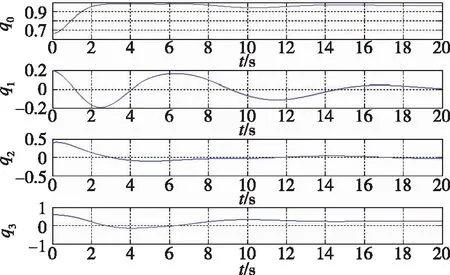
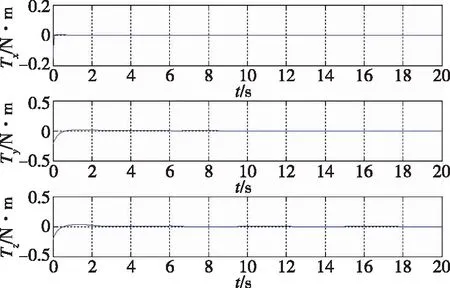
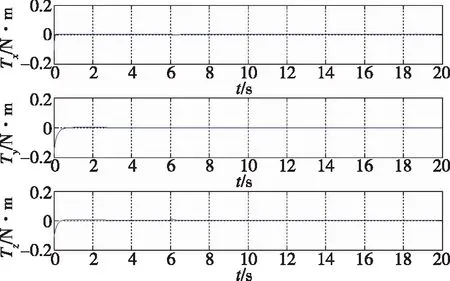
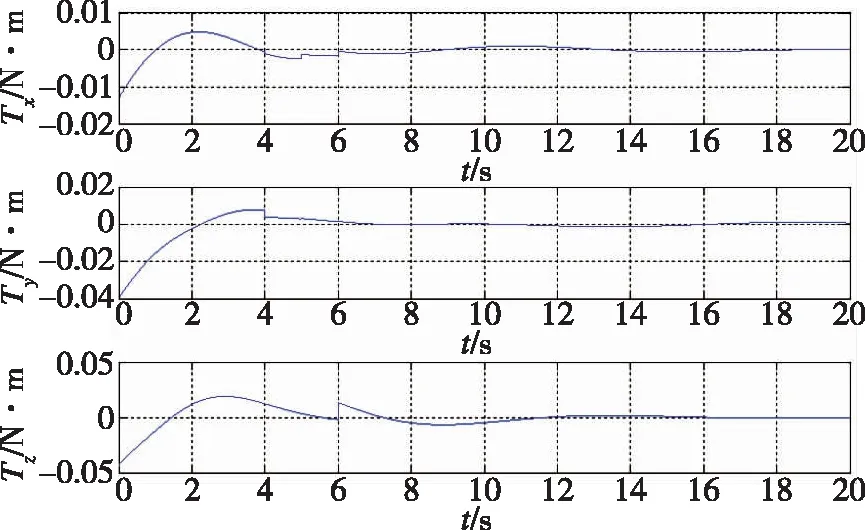
式(23)中,c2为正实数,e为正实数,且满足0 (24) 将式(24)代入式(22)中,可得 (25) 式(25)中,矩阵R1可写为 (26) 由不等式可得 (27) 式(27)中,κ=min{1,c1}。 假设1:由于干扰力矩Td是有界的,则可以合理地推测存在正常数dmax,满足 (28) 式(28)中,参数ρ≥1为给定正常数。 代入式(27),则可知Lyapunov函数V2的导数有界如式 ≤0 (29) 则闭环系统渐近稳定。 备注:定理1所给出的控制方法存在与q0相关的函数H(q0)尚未给出,但不影响对该系统稳定性的论证。换言之,只要函数H(q0)满足条件(1)、(2)、(3),则该闭环控制系统是渐近稳定的。对H(q0)的论证将在下一节给出。 表1 文献中常用的H(q0)的选取方法 由表 1可以看出,很多方法是基于误差空间函数的衍生来描述势能损耗的。例如,编号(1)就考虑了一种基于几何学的姿态控制方法,其势能部分的构造是基于姿态四元数误差的二范数;编号(4)则直接基于四元数误差矢量求得。然而,这两种构造方法都不是几何构型中路径最短的选择。空间误差的消除方法主要为平衡误差方法,从几何层面上看,方向余弦矩阵是描述航天器姿态最直接的手段,可以快速地平衡和消除空间误差。通过对方向余弦矩阵进行变体考虑,虚拟控制律为 (30) 则有 (31) 对式(31)进行积分,可得 (32) 等价于 (33) 也等价于 (34) 式(34)中,符号函数sgn的定义为 (35) (a)H(q0)的曲线 (b) 的曲线图2 H(q0)的曲线及其对q0的导数Fig.2 Function H(q0) and its derivative to q0 (36) 将其对q0求导可得 (37) H(q0)函数(36)及其导数的图像如图 3中所 (a)H(q0)的曲线 (b) 的曲线图3 H(q0)的曲线及其对q0的导数Fig.3 Function H(q0) and its derivative to q0 (38) (39) 式(39)中,c1>0、c2>0均为给定正实数,则闭环系统全局稳定。 已由前文证毕。 为了验证该方法对执行机构安装偏差及故障的处理能力,假设飞轮的故障及安装偏差为: ①X轴飞轮在5s后输出力矩降低,e1(t)=0.6,安装偏差α1=10°,β1=12°; ②Y轴飞轮在4~20s之间输出力矩降低,e2(t)=0.5,安装偏差α2=8°,β2=15°; 分别采用控制律如定理二(即式(38)和式(39),下称控制方法一)、控制律如定理一(即式(12)和(13),其中H(q0)=1-q0,下称控制方法二)以及PD控制(下称控制方法三)3种控制方法对上文的卫星系统进行数值仿真,以比较说明本文所提出的控制方法对存在飞轮偏差及故障的卫星的姿态控制能力,以及不同的H(q0)对控制方法的影响。 (a)由控制方法一仿真所得的角速度曲线 (b)由控制方法二仿真所得的角速度曲线 (c)由控制方法三仿真所得的角速度曲线图4 由三种控制方法仿真所得的角速度曲线Fig.4 Angular velocity of three control methods (a)由控制方法一仿真所得的四元数曲线 (b)由控制方法二仿真所得的四元数曲线 (c)由控制方法三仿真所得的四元数曲线图5 由三种控制方法仿真所得的四元数曲线Fig.5 Quaternion of three control methods (a)由控制方法一仿真所得的飞轮输出力矩曲线 (b)由控制方法二仿真所得的飞轮输出力矩曲线 (c)由控制方法三仿真所得的飞轮输出力矩曲线图6 由三种控制方法仿真所得的飞轮输出力矩曲线Fig.6 Control torque of three control methods 由仿真结果可以看出,在考虑飞轮存在安装误差及故障的情况下,传统的PID控制难以维持航天器系统姿态的稳定。本文所提出的反步容错控制方法如定理一(即式(12)和(13)),无关于H(q0),在飞轮存在安装误差及故障的情况下能够有效实现容错控制,确保航天器姿态的稳定性。选择不同的H(q0),对系统达到稳定状态的时间会有较大影响,这是由误差空间中势能损耗的平衡路径决定的。当用基于方向余弦的矩阵来描述航天器势能损耗(即选择H(q0)如式(36)所示)时,系统仅需6s即可达到稳定,而用基于四元数误差的二范数描述势能(即H(q0)=1-q0)时,系统需要12s才可达到稳定。在相同条件下,基于方向余弦矩阵所建立的控制方法的调节时间快了1倍。提高控制方法的调节时间,可以确保航天器在突发故障的情况下具备快速机动能力,从而提高系统的安全性。 (1)本文提出了一种航天器姿态反步容错控制方法,以飞轮作为航天器执行机构,在考虑飞轮存在安装偏差及存在反作用力矩降低、对控制信号无响应、输出力矩叠加偏差、反作用力矩等不确定故障的情况下,仍能够保证航天器姿态的稳定性,具有良好的容错能力和鲁棒性; (2)针对反步容错控制方法的误差空间收敛能力开展了进一步讨论,基于方向余弦矩阵来描述航天器势能损耗,能够提高控制方法误差收敛的效率,从而保证航天器在存在较大初始姿态偏差或突发性故障的情况下,具备姿态快速回转的机动能力,进而提高系统的安全性。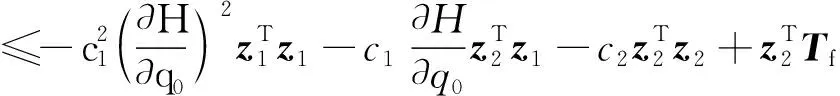
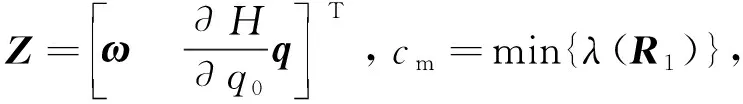
2.2 基于误差空间定义H(q0)函数


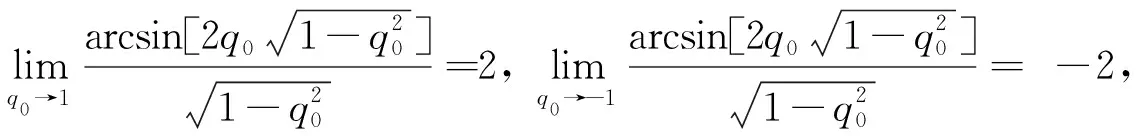
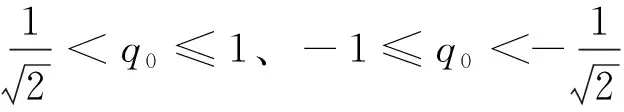
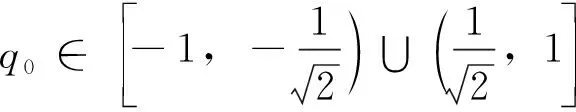

3 仿真分析
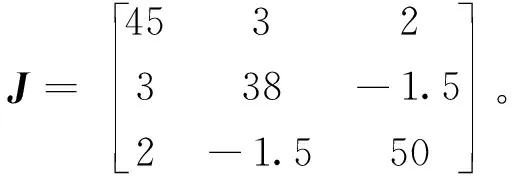
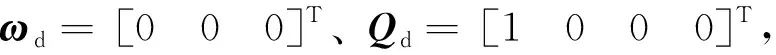
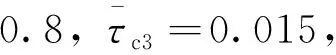
4 结 论

