吊舱平台微电机转子系统的分岔特性分析*
江乐果,王一波,焦 彤,胡百振,孟祥福
( 1.上海航天控制技术研究所·上海·201109; 2. 中国航天科技集团有限公司红外探测技术研发中心·上海·201109)
0 引 言
在现代战争中,精确制导武器在局部战争中对于各国夺取主动权起到了至关重要的作用。由于在制导精度、灵敏度及抗干扰能力等方面的突出优点,红外探测技术已经成为了国内外一个重要的研究方向,其中光电吊舱承担着制导系统的关键作用。吊舱平台随动系统的作用是保持探测器的稳定,通过在视场内搜索、捕获及跟踪目标,为末段制导提供弹体的位姿信息。
在弹体主发动机工作过程中,高速弹旋制约着制导系统的探测性能,通过微电机转子系统的消旋作用,为光学探测器提供可靠的工作平台保障。当制导系统跟踪目标时,红外探测器将目标视线与光轴的偏差角信息提供给控制电路,从而产生相应的控制电流并输送至力矩器。在力矩作用下,陀螺平台转子轴向目标方向进动,形成闭合回路,实现对目标的实时跟踪。因此,微型电机转子系统的稳定特性将影响到整个吊舱平台的跟踪性能,通过分析平台的非线性动态特性,对弹体制导精度的提高有着十分重要的作用。
1 框架式稳定平台的非线性动力学模型
吊舱平台电机转子系统通过一对滚动轴承支承转子及稳定平台,其构成了刚性转子系统模型,吊舱平台微电机转子模型如图1所示。在模型当中,需综合考虑转子组件的质量不平衡、滚动轴承的内部游隙等要素对系统的非线性影响。轴承外圈刚性固定支承在制导框架系统上,内圈与转子轴固联在一起,钢球在套圈滚道间做纯滚动。

图1 光电吊舱平台微电机转子系统模型图Fig.1 Model diagram of micro-motor rotor system of optoelectronic pod platform
1.1 电机转子轴承的非线性接触力
由滚动轴承的运动学理论可知,假设滚动体通过保持架等距离分布在内、外圈滚道之间,并在滚道内做纯滚动,如图2所示。在忽略润滑油膜影响的前提下,滚动体的中心角速度wcage=wrotorRi/(Ri+Re)。其中,wrotor为吊舱平台的转子角速度,吊舱平台角速度可转换为转速nrotor,换算关系为:nrotor=wrotor/(2π);Re为外圈滚道半径;Ri为内圈滚道半径。

图2 滚动轴承非线性接触模型示意图Fig.2 Schematic diagram of nonlinear contact model of rolling bearing
由Hertz 接触理论可知,滚动体与内外滚道的局部弹性接触力F与弹性接触变形量相关,轴承的x和y方向上的接触力分别为
(1)
式(1)中,Fx和Fy分别表示滚动体与滚道间的弹性恢复力在水平和垂直两个方向上的分量,x和y分别表示轴承内圈质心点在水平方向和垂直方向上的位移,θi为第i个滚动体的方位角,Kc为球与滚道的接触刚度,γ0表示轴承的径向间隙。其中,(Δ)+表示括号内的值为非负,即当Δ≤0时,轴承中第i个滚动体未处于载荷区内,对应的滚动体与滚道间的弹性接触变形为0。
根据Hertz接触理论,点接触类型的两物体的接触刚度可表示为
(2)
式(2)中,E为材料的弹性模量,μ为材料的泊松比,∑ρ为接触点的曲率和,δ*为接触变形系数。
因此,滚动体与滚道间的接触刚度可表示为
(3)
式中,ke表示滚动体与外圈的接触刚度,ki表示滚动体与内圈的接触刚度。
第i个滚动体的方位角θi可表示为
建设绿色矿山、发展绿色矿业是矿业行业当前的必然选择和唯一选择,是矿业行业落实新发展理念的具体行动。建设绿色矿山,大力发展循环经济,协调矿山资源环境之间的关系,是树立起良好形象、实现转型升级的重要方式。
(4)
其中,Nb为滚动体的个数,t为转子运行时间。
光电吊舱微电机转子系统的动力学方程为
Fr+Meewcage2cos(wcaget)
Meewcage2sin(wcaget)
(5)
式中,Me为转子系统质量,C为转子系统阻尼系数,Fr为作用在转子上的恒定径向载荷,e为转子系统不平衡偏心距。
1.2 转子非线性分岔与混沌理论
1.2.1 分岔
分岔是带有参数的动力系统随着参数的变化,做出的相应的定性行为和定量行为。
定义:考虑含有参数的常微分方程组
其中,J是开集,x是状态变量,u是分岔参数。当u连续地变动,如果系统的定性行为发生突然变化,则系统在uo处将发生分岔,uo∈J。该系统的定性或定量行为随参数u的变化而变化的图形即为分岔图。
1.2.2 混沌
混沌运动是一种不稳定有限定常运动,为全局压缩和局部不稳定的运动。混沌的复杂性一般可通过时间历程图、相图、庞加莱(Poincaré)截面法等特征表现出来,利用一定的理论方法可解析证明系统的混沌特性。
设∑⊂Rn是某一n-1维超曲面的一部分,若对于任意的x⊂∑,∑的法向量n(x)满足与向量场f(x,u)的无切条件
nT(x)·f(x,u)≠0
则称∑是向量场f(x,u)的Poincaré截面。可根据Poincaré截面的情况来判断系统的运动特性,当截面上有一个不动点时,系统处于1周期运动;当截面上有n个不动点时,系统为n周期运动态;当Poincaré截面出现一封闭曲线时,系统为拟周期运动;当截面上为有界无穷的点集合时,系统为混沌态。
2 转速对吊舱电机转子系统的影响分析
根据文中1.1节的内容对转子系统的非线性模型进行了分析,着重考虑了转速对吊舱电机转子系统的影响,探讨出了不同转速变化范围下的转子系统稳定性影响,从而在设计中可避免混沌分叉效应对吊舱平台跟踪精度及稳定性的影响。在满足光电吊舱稳定平台启动力矩使用要求的前提下,以某型号微型电机球轴承为例进行了分析,其特征参数为:滚动体数Nb=8;外圈沟道半径Re=2.25mm;内圈沟道半径Ri=3.75mm;阻尼C=50.0Ns/m;径向游隙γ0=5μm;吊舱平台系统的质量Mplatform=0.15kg。
吊舱平台的稳定性会随着微型电机转子系统的转速而发生变化,从而影响到安装在稳定平台上的光电探测系统的跟踪稳定性。在吊舱电机转子系统承受的探测器平台等的系统质量及等效阻尼确定的情况下,将电机控制转子的转速作为变量参数(取值范围为:500r/min~15000r/min)可研究微型电机在从低速启转至高速转动的过程中,系统的稳定响应状态。通过对式(5)的动力学方程进行求解,可得到转子系统的位移、速度等参数随转速变化的Poincaré 图及分岔图。图3为框架平台转子系统的中心在x方向上的位移-转速分岔图,图3给出了不同转速下转子中心的 Poincaré 图和质心轨迹图。
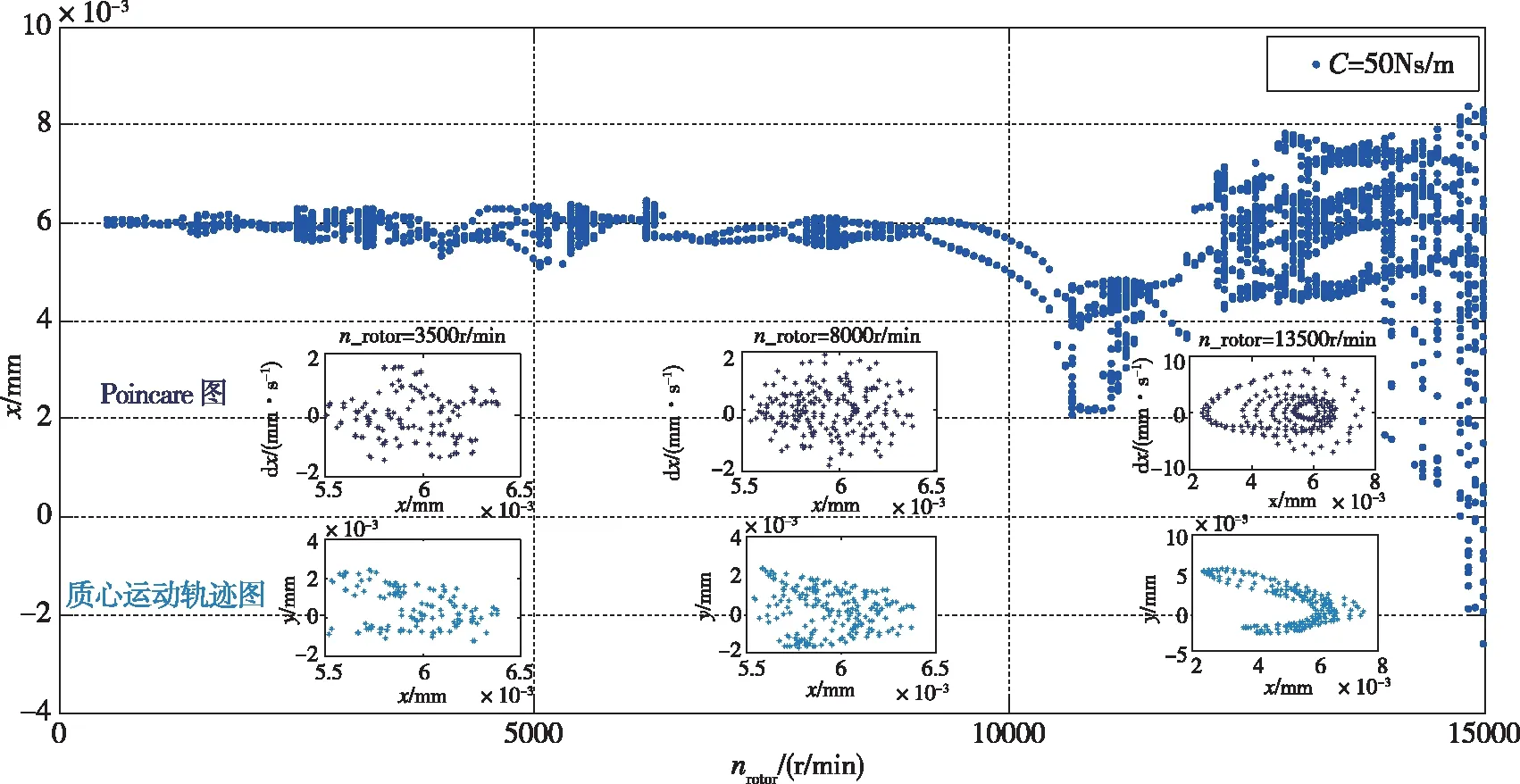
图3 x方向上的位移转速分岔图Fig.3 The bifurcation diagram of displacement and rotational speed in the x direction
从图3可见,在转速变化过程中,吊舱平台系统的运动十分复杂,系统经历了多周期运动、拟周期和混沌态交替变化的过程。在500r/min≤nrotor≤2500r/min时,系统处于多周期运动状态;在2500r/min≤nrotor≤6500r/min时,系统处于小范围混沌态响应状态;在7000r/min≤nrotor≤11000r/min时,系统进入到拟周期态;当11000r/min≤nrotor≤12500r/min时,系统进入到多周期态;当进一步提高转速时,转速12500r/min≤nrotor≤15000r/min时,系统进入多周期及混沌态交替混合区,对探测器对目标的稳定跟踪造成了较大影响。
(a)当nrotor=3500r/min时,x方向上的Poincaré截面图中的动点无规则分散在速率为±2000μm/s的小范围内,转子的质心轨迹在水平x和垂直y方向的跳动范围分别为(-0.5μm,0.5μm)和(-1.5μm,2.5μm),表明系统处于多周期运动态。
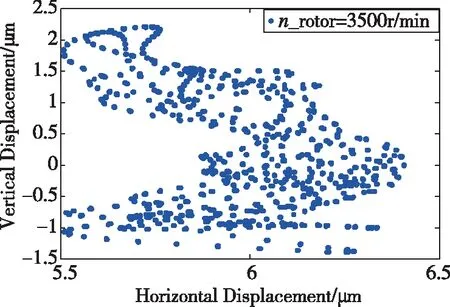
图4 nrotor=3500r/min时的质心运动轨迹图Fig.4 Centroid motion trajectory diagram at nrotor=3500r/min

图6 nrotor=3500r/min时的水平x方向时域图Fig.6 Time-domain diagram in the x direction at nrotor=3500r/min

图7 nrotor=3500r/min时的垂直y方向时域图Fig.7 Time-domain diagram in the y direction at nrotor=3500r/min
(b)当转子速度nrotor=8000r/min时,由Poincaré图和质心轨迹图可知,转子质心在小范围内运动。Poincaré图的变化呈现出发散的趋势,系统运动呈现出轻微向外发散的过程,系统处于窄范围混沌态。

图8 nrotor=8000r/min时的质心运动轨迹图Fig.8 Centroid motion trajectory diagram at nrotor=8000r/min

图9 nrotor=8000r/min时的Poincaré图Fig.9 Poincaré diagram at nrotor=8000r/min
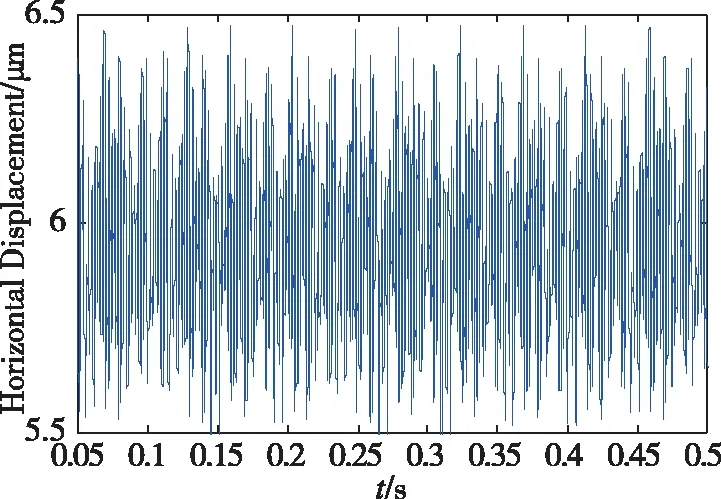
图10 nrotor=8000r/min时的水平x方向时域图Fig.10 Time-domain diagram in the x direction at nrotor=8000r/min

图11 nrotor=8000r/min时的垂直y方向时域图Fig.11 Time-domain diagram in the y direction at nrotor=8000r/min
(c)当转速nrotor=13500r/min时,Poincaré图形成了一个明晰的多重封闭曲线,这表明平台转子系统处于一个多周期状态,转子质心也做近似规则的运动。水平x和垂直y方向的时域图表明系统长时间处于低幅值跳动状态,在其余工作时间内有规则地跳动到较大幅值区域。

图12 nrotor=13500r/min时的质心运动轨迹图Fig.12 Centroid motion trajectory diagram at nrotor=13500r/min

图13 nrotor=13500r/min时的Poincaré图Fig.13 Poincaré diagram at nrotor=13500r/min
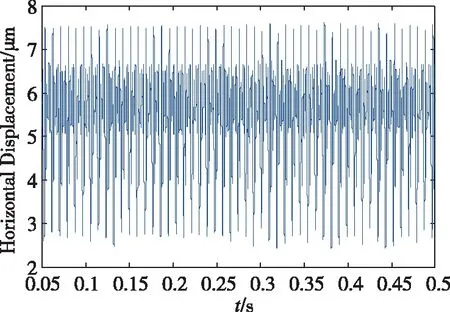
图14 nrotor=13500r/min时的水平x方向时域图Fig.14 Time-domain diagram in the x direction at nrotor=13500r/min

图15 nrotor=13500r/min时的垂直y方向时域图Fig.15 Time-domain diagram in the y direction at nrotor=13500r/min
3 结 论
随着转子转速的变化,光电吊舱平台电机转子系统的响应可能会出现周期、拟周期、分岔和混沌的振动状态。在转子系统的动力学分析中,滚动轴承的接触刚度、径向游隙、不平衡质量和滚动体的个数等参数都会影响整个稳定平台系统的非线性动态特性。在对红外光电吊舱系统进行设计的过程中,需要充分考虑微型电机转子系统的非线性分岔特性。通过调整轴承转子的内部刚度特性,使转子系统尽量避开混沌分岔工作的转速范围,进而可确保制导系统的探测精度。

