低渗油藏空气泡沫驱提高采收率潜力评价新模型

张 冰，金 志，白慧芳，王成俊.

(1.陕西延长石油(集团)有限责任公司销售公司，陕西西安 710075；2.陕西延长石油(集团)有限责任公司研究院，陕西西安 710075)

空气泡沫驱创造性地将空气驱和泡沫驱有机地结合起来，它综合了泡沫驱与空气驱的优点，成本很低(国外现场试验资料报道注入成本 0.018美元/m3)，增油效果明显，空气泡沫驱提高采收率技术尤其适用于非均质强的低渗透油藏。从目前矿场试验和应用的效果来看，延长油田、胜利油田、百色油田、中原油田等先后在低渗油藏实施了空气泡沫驱[1-10]，并取得了一定效果，证明了该技术在低渗透油藏中具有良好的适应性和应用潜力。公开报道的低渗油藏空气泡沫驱潜力评价方法计算要求数据量大，计算过程复杂，计算时间耗费过长，不利于研究人员和现场工程师快速掌握和评价[11-14]。因此，为了快速预测待实施空气泡沫驱区块的提高采收率的潜力，建立一套计算快速、计算结果可靠的潜力评价方法十分必要。

1 潜力评价数学模型

1.1 基础评价模型

空气泡沫驱油过程和水驱油近似，泡沫溶液进入含油区，不能将油全部驱替出去，是一个非活塞驱油过程。通过贝克莱-列维尔特驱油理论方程定量描述这一过程，在此基础上，用一维驱替数学模拟计算代替二维平面驱替数学模拟计算，使模型相对简化，从而建立出相对准确、易于求解的空气泡沫驱潜力评价基础模型。

1.1.1 模型的假设条件

(1)油藏属于多孔介质，不考虑上覆岩层压力等因素对油藏的压缩；

(2)不考虑外来力对储层流体的压缩；

(3)油水渗流为稳态渗流；

(4)油藏含有2个以上储层，各储层渗透率不同，存在明显的非均质性；

(5)不考虑重力和毛管力。

1.1.2 贝克莱-列维尔特模型[15]

(4)

其中，Sw、tD、Fw和xD分别为含水饱和度(小数)、无因次时间、水相分流量(小数)和无因次距离。

其中，无因次距离xD用下式计算：

(5)

其中：xD、P、φ、A和S分别为无因次距离、流管孔隙体积(m3)、孔隙度(小数)、渗流面积(m2)和渗流距离(m)。

tD为无因次时间，公式(6)计算：

(6)

其中，tD、t、ΔQ和PV分别为无因次时间、渗流时间(s)、0到t时间累积总流量(m3/s)和流管孔隙体积(m3)。

其中流管的孔隙体积用用下式计算：

(7)

1.1.3 分流量模型

(1)

其中，fi、Qi和Qt分别为i相的分流量(小数)、i相的流量(m3/s)和总流量(m3/s)。

i相的相对分流量用λri表示，公式如下：

(2)

其中，Kri和μi分别为i相相对渗透率(小数)和i相黏度(MPa·s)。

总相对分流量以λrt代表，公式如下：

(3)

其中，Kri、μi和N分别为i相相对渗透率(小数)、i相黏度(MPa·s)和通过渗流截面的相数(整数)。

1.2 基础评价模型的修正

基础评价模型没有考虑低渗油藏特有的渗流特征和空气泡沫驱油机理。因此，通过引入低渗储层启动压力梯度、应力敏感系数及泡沫吸附、界面张力效应和流动减小因子(半衰期、遇油消泡)等影响因素对基础模型进行修正。

1.2.1 考虑黏性指进和纵向非均质性影响的计算模型

由于低渗油藏储层非均质性[16]导致在空气泡沫驱过程中，存在黏性指进现象，因此，本文通过引入系数K对采收率进行修正。

(8)

其中，K代表Koval系数、H代表非均质性系数；原油黏度和注入泡沫黏度分别以μo和μs代表(MPa·s)。

1.2.2 考虑低渗储层启动压力梯度和应力敏感的计算模型

考虑应力敏感与启动压力梯度的影响，通过引入介质变形系数[17-18]和启动压力梯度，修正渗流方程，并嵌入提高采收率计算模型中，进而达到对产量和注入量进行修正[19]。

(9)

其中，pi、pw分别为地层孔隙压力和井底流体压力(MPa)；由于应力敏感导致介质变形，以系数αk代表(MPa-1)；q为空气泡沫驱过程中油井单井日产量(m3/d)；μo为原油黏度(MPa·s)；Ki为未发生介质变形的初始渗透率(10-3μm2)；h为有效地层厚度(m)；rw为油井的半径(cm)；re为设定油藏的边界(cm)；由于低渗油藏存在启动压力梯度，以G代表(MPa/m)。

1.2.3 考虑泡沫吸附的计算模型

通过引入吸附模型[20](美国能源局)，将注入泡沫浓度、性质和岩石相关性质考虑其中，从而定量表征空气泡沫驱油过程中的吸附效应，从而实现对采收率进行修正。

(10)

其中，DS为泡沫和储层岩石发生吸附效应后吸附浓度之比；As为黏土矿物所占整个储层的比例(一般采用默认值，0.33)；Cs、φ分别为泡沫液注入时的浓度和储层的孔隙度；ρswf和ρrock分别为储层岩石的密度(g/cm3，默认值为2.68)和泡沫溶液注入时的密度(g/cm3，默认值为1)；体积浓度，无单位。

1.2.4 考虑泡沫的界面张力效应对相渗变化的计算模型

空气泡沫驱过程中，由于起泡剂是表面活性剂，有降低油水界面张力的作用，从而提高驱油效率，因此，本文引入Schechter计算模型[21]定量表征界面张力效应。

(11)

其中，σos、σminos、σmaxos分别为瞬间油与泡沫间的界面张力、最小的油与泡沫间界面张力和最大油、泡沫间的界面张力(mN/m)；Cσos、Cσminos、Cσmaxos分别为泡沫液的瞬间注入浓度、最小的油与泡沫间界面张力时的注入泡沫液的浓度和最大油、泡沫间的界面张力时注入泡沫液的浓度；es为特定值，一般设定为1。

油水相对渗透率会因界面张力的变化而发生变化，本文利用修正的Todd-Longstaff方法计算修改相对渗透率。

(12)

(13)

Soros=Sor·F

(14)

Kr=F·Krow+(1-F)Krws

(15)

其中，F为修正后相渗系数；σref为设定的界面张力(mN/m)；Soros为空气泡沫驱后的残余油的饱和度；Sor为空气泡沫驱前的残余油的饱和度；Kr为空气泡沫驱时油相相对渗透率(10-3μm2)；Krow为注水开发时油相相对渗透率；Krws为空气泡沫驱过程中混相时油相相对渗透率。

1.2.5 考虑泡沫半衰期等因素的计算模型

空气泡沫驱过程中，泡沫遇水气泡，遇油消泡，泡沫存在半衰期，而泡沫具有降低油水流度比的作用，从而抑制气窜，因此，引入流度减小因子表征这一机理。

(16)

(17)

(18)

(19)

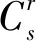
2 模型的可靠性验证与应用

利用评价模型对油田进行南泥湾新窑区油藏进行模拟评价，参考延长油田空气泡沫驱提高采收率方法实际实施参数，即日注入量40 m3，注入浓度0.005%，注入段塞比0.25，累计注入量1PV为输入参数；通过潜力评价模型计算采收率的结果与商用软件Eclipse的计算结果进行对比，两者结果非常接近，误差在5%以内(图1)，因此，潜力评级计算模型的结果是可靠的。区别在于，商用软件采用的有限差分方法，并考虑了毛管效应等因素的影响，而新模型将启动压力梯度和应力敏感系数考虑其中，使数值偏小，但计算速度快于商用软件，ECLIPSE运算时间为1分钟，新模块运行计算时间仅为5秒，计算速度明显加快，如果应用于多个区块的潜力评价，时间优势更为明显。因此，在低渗油藏空气泡沫驱提高采收率潜力评价时，需考虑低渗油藏特有的渗流特征，否则结果会偏大。

图1 空气泡沫驱提高采收率潜力评价结果对比Fig.1 Comparison of evaluation results of air foam flooding enhanced oil recovery potential

应用新模型和ECLIPSE软件分别计算延长油田待评价6个区块空气泡沫驱提高采收率潜力评价值，这6个区块油藏参数见表1，计算结果见表2。

从表2计算可以看出，空气泡沫驱提高采收率幅度均超过了5%，表明6个区块空气泡沫驱提高采收率潜力是巨大的，是可以开展现场试验的，而且因为油藏储层物性较好、含油饱和度较高、地层能量更为充足，且水驱效果较好的区块，采收率提高幅度会更大，更适合开展空气泡沫驱。

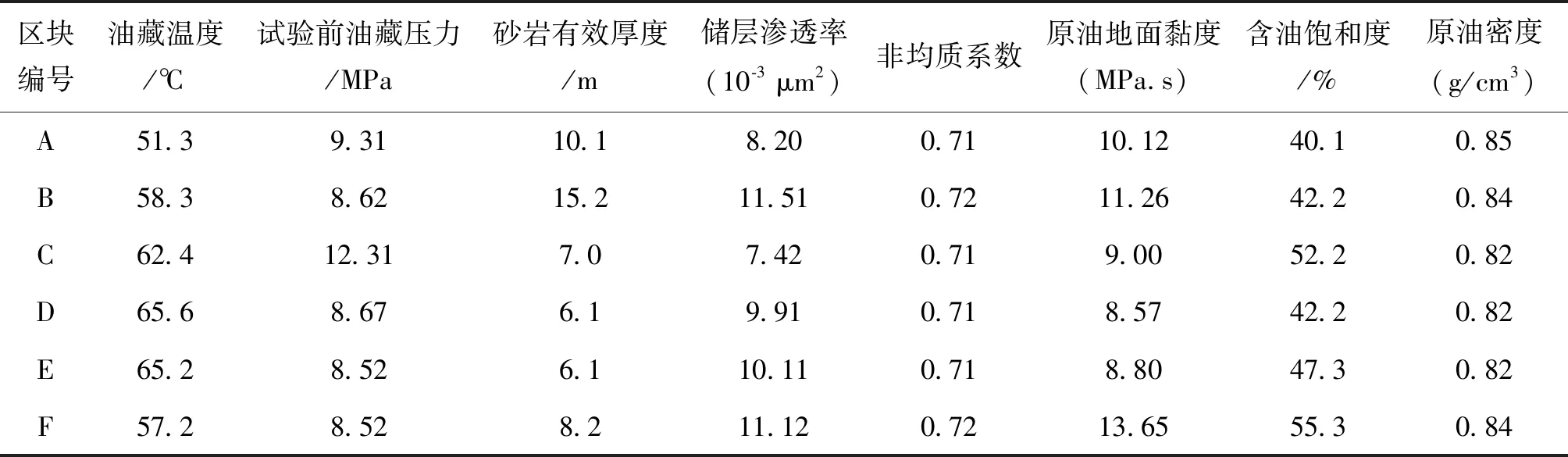
表1 待评价6个区块油藏参数(引用要加说明)Table 1 Reservoir parameters of six blocks to be evaluated

表2 6个典型区块空气泡沫驱潜力评价结果Table 2 Evaluation results of air foam flooding potential in six typical blocks

3 结论

(1)新模型综合考虑低渗油藏渗流特征(启动压力梯度、应力敏感)和空位泡沫驱油机理(降低油水界面张力、吸附、半衰期)等，将部分渗流特征简化，以一维代替二维，使计算过程简化，计算速度较商用软件快10倍以上。

(2)分别用空气泡沫驱潜力评价模型和商业数值模拟软件Eclipse对南泥湾新窑区油藏进行空气泡沫驱潜力评价，结果新模型计算速度远大于Eclipse，并且计算结果基本一致，误差在5%以内，表明新模型可靠程度高，可以应用于现场。

(3)通过模型的应用结果显示，延长油田6口典型区块空气泡沫驱提高采收率潜力是巨大的，超过了5%。随着空气泡沫驱在低渗油藏的推广，空气泡沫驱提高采收率潜力评价方法能够很好地为矿场应用提供参考。