含水率变化对西安地区深基坑土钉支护稳定性的可靠度影响研究

张宏刚

(1.中煤科工集团西安研究院有限公司 工程地质研究所， 陕西 西安 710077；2.西安理工大学 岩土工程研究所， 陕西 西安 710048)

西安是我国黄土分布最广的地区之一，随着城市基础建设规模的不断扩大，出现了大量典型的超深、超大基坑，而基坑支护首当其冲，土钉支护以其施工效率高、工艺简单、可靠性好、造价低等优点而被大量应用。工程实践表明，约30%的支护工程变形破坏都不同程度与水有关[1-2]，而黄土是具有多孔、多相、松散、结构性强[3]的典型属性，与水作用后其物理力学参数将产生显著变化，该变化进而诱使和导致土钉支护结构产生各种破坏模式，因此黄土的工程效应已成为支护工程设计与稳定性评价的热点问题。

国内外学者关于含水率对土体强度的影响做了一定的研究工作。孙强[4]在文中指出地下水影响了土体与支护结构的受力状态，引起土体与支护强度的降低。叱干晓敏[5]在文中认为含水率变化对边坡安全系数影响显著，随含水率的增加,安全系数变化速率均逐渐减小。盛维高等[6]在文中建立了非饱和土含水率与强度的关系式，并用其分析了某高边坡的稳定性，提出把含水率作为边坡稳定分析的重要参数。成立芹[7]在文中分析了地下水渗流对基坑稳定性影响，求得了地下水渗流对基坑稳定性影响规律。廖红建等[8]在文中利用改进的直剪仪进行一系列不同含水率的土体和混凝土试块复合体的剪切试验，研究了混凝土桩土复合体的剪切应力-应变关系，得出了强度指标与含水率的变化规律。柴寿喜等[9]在文中对三种含水率下稻草加筋土的相关试验研究得出随含水率的增加，加筋土的强度降低，抗变形能力减弱。张宏刚等[10]在文中分析探讨了土体含水率变化对土钉支护失效模式的影响以及稳定性变化规律。

郭震山[11]在文中得出了随降雨历时增加，湿润锋线不断向黄土坡体内部推进，非饱和区基质吸力减小，边坡安全系数降低。高帅等[12]在文中研究了泾阳县某边坡原状黄土在不同含水率、不同固结围压下的强度和变形特性，得出黏聚力随着含水率的增大显著降低而内摩擦角所受影响较小。周学[13]在文中研究得出了成都地铁场站基坑膨胀土抗剪强度指标以及膨胀力的变异性对基坑支护结构抗倾覆稳定可靠性指标β的影响规律。郭林坪等[14]在文中对土工试验数据的统计规律做了深入分析，详细研究了天津滨海新区黏性土物性指标之间及其与力学指标间的相关关系，给出了指标之间的经验关系式。屈若枫等[15]在文中分析了武汉地区深厚淤泥质土物理力学参数及其指标间的相关性，提出天然密度、干密度、液限、塑限、饱和度等服从正态分布。张秀丽[16]在文中归纳出黏聚力、内摩擦角与含水率呈二次抛物线关系，得到了考虑含水量和干密度影响的压实黄土抗剪强度计算公式。

基坑支护的稳定评价前人虽做了一定的相关研究工作，但多数仍依据传统的极限平衡理论，采用稳定系数判定基坑支护工程的稳定性。传统理论方法从一定程度上虽然能够判定基坑支护工程整体的稳定性，但由于岩土体材料自身具有变异性强、随机性大、强度指标受控因素多、岩土计算模型过于简化等问题，常使支护工程的计算与设计依据不充分而偏于保守。为克服传统评价方法的不足，较系统的评价支护工程的稳定性，岩土工程界已开始应用可靠度理论分析岩土支护工程稳定性。

曹净等[17]在文中采用改进响应面法研究土层抗剪强度指标c、φ间的互相关性对基坑支护结构可靠度的影响做了分析，认为相关性对可靠指标有显著影响。吴坤铭等[18]在文中以可靠度理论为基础采用一阶可靠度分析方法进行了基坑土钉支护可靠度计算，把计算参数视为随机变量，考虑参数变异性对基坑土钉支护可靠度的影响。何渊[19]在文中对深基坑土钉支护结构稳定性的可靠度与模糊可靠度做了研究。李健等[20]在文中得出了锚杆支护结构可靠度指标β与锚杆参数的相关关系，认为锚杆直径与间排距对支护结构的可靠性影响最大。李典庆等[21]在文中提出边坡系统失效概率随锚杆握裹层厚度的增加而减小，随注浆体水灰比的增加而增大；吴振君等[22]在文中对边坡可靠指标在临界滑面上的不同位置上的敏感性做了分析与尝试。许梦国等[23]在文中提出了基坑支护系统稳定性的可靠度模型，并对其做了验证分析。王建华[24]在文中运用Monte-Carlo法计算了基坑支护体系的可靠性指标与失效概率。张琳等[25]在文中提出了支护体系可靠性的目标值。廖瑛[26]在文中采用JC法计算了基坑稳定可靠指标，得出了在多元失稳模式下基坑支护结构失稳的概率范围。

支护工程稳定的可靠度研究仅在隧道、矿井巷道支护中有少量报道，而将土工试验与可靠性理论相结合研究黄土地区基坑支护稳定可靠度的研究鲜有报道。本文以西安一深基坑土钉支护工程为例，分析探讨含水率对基坑土体强度指标和各失效模式可靠度的影响规律，尝试为西安黄土区土钉支护结构的稳定性评价提供一种参考依据。

1 试验与工程概况

1.1 试样制备

试验用土取自西安仁厚庄某安置楼基坑场地，试验前经测其饱和含水率为31.8%，干密度为1.59 g/cm3，液限为28.59%，塑限为19.35%，塑性指数9.24，液性指数为0.45，土样直径为39.1 mm，高度80 mm。制样前先对取回的黄土过筛，之后将其含水率统一调配至12%，并保湿密封保存48 h，最后将试样含水率分别增湿至12%、15%、18%、21%、24%、27%、30%七个等级，为使试样内部水分均匀吸收，采用分时段点滴水分，每级含水率下制标准样5个。

1.2 试验方案

增湿配制成7级含水率的重塑土样，进行不固结不排水(UU)三轴压缩试验，根据土体赋存的地质条件，试验围压分别设为100 kPa、200 kPa、300 kPa。

试验剪切速度设为0.276 mm/min，启动电动机，合上离合器，开始试验。试样每产生0.2 mm变形量，测力计和百分表记录一次数据，当测力计读数出现峰值时，剪切进行到轴向应变为15%时，认为试验结束。加载过程中记录量力环读数，计算主应力差。

1.3 工程概况

该土钉支护工程位于西安市仁厚庄，是多栋高层建筑的基础工程部分，基坑深7.15 m，坡度系数为0.2，从上至下共布设4排土钉。地表以下75 m范围内的岩土勘察表明：勘察区内地基土由上至下分别是填土(0.40 m～4.20 m)、黄土(0.70 m～11.90 m)、古土壤(14.8 m～17.20 m)、粉质黏土(10.50 m～75.00 m)，经现场试验测定各土层含水率分别为18.5%、23.6%、19.4%、24.1%，稳定水位在地表以下2.60 m～4.20 m范围内。基坑开挖支护过程中频受降雨及地下水变化影响，现场监测显示土钉墙多处出现局部土体垮落、墙体变形现象。

1.4 试验结果及分析

通过三轴压缩试验读取量力环的数据，根据摩尔-库仑破坏标准，做出土体在3种围压下的应力摩尔圆，得出7种含水率下土体强度指标，强度指标与含水率曲线关系如图1、图2所示。

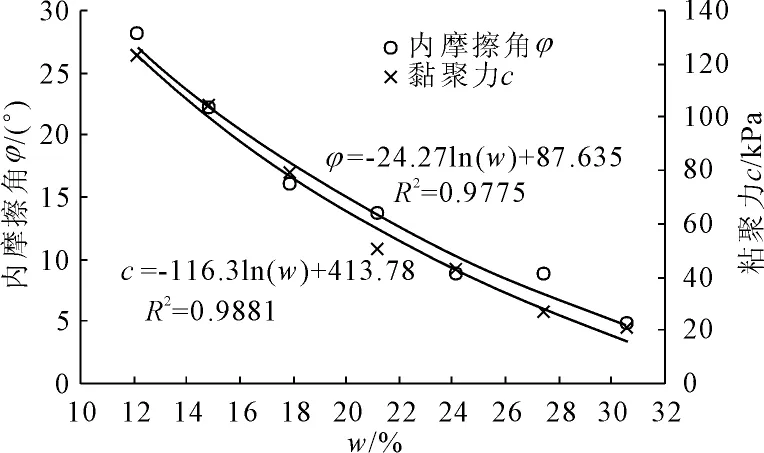
图1 黏聚力、内摩擦角与含水率曲线关系

图2重度与含水率曲线关系

由试验结果可知：随着含水率的增加，黏聚力c与内摩擦角φ的大小在不断降低；含水率约在24%之前时c，φ值的衰减幅度非常显著，之后c，φ值衰减趋向平缓。黏聚力c降低幅度明显大于内摩擦角φ，说明含水率变化对黏聚力的弱化程度要明显强于对内摩擦角的影响，进一步说明黏聚力c对水的敏感程度要强于内摩擦角φ。

通过上述试验数据分析，发现西安黄土的水敏性很强烈，黄土体参数c、φ、γ随含水率的增加出现了不同程度的衰减。主要原因在于黄土遇水作用后其内部结构产生损伤和破坏，承担抗力的微观结构与骨架在逐渐损伤和累积，进而导致周围骨架连接力在不断降低，同时由于骨架颗粒间的接触面在水分的浸渗下，使黄土内含有的像蒙脱石等亲水物质不断溶解、分解，水膜的楔入进一步弱化土颗粒间的连接强度，在较小压力下这些接触点或产生断裂或产生错动，结构连接不断遭受破损，强度逐渐降低；由曲线不难发现，试样含水率约在24%前强度衰减比较快，原因是在24%前土体的微细观结构已遭大部分破坏，含水率在24%之后残余未损的结构对水的敏感性已明显减弱，表现为强度衰减缓慢。

2 可靠度理论简介

结构在规定的条件与时间内完成预定功能的能力谓之可靠性，在规定的条件与时间内完成预定功能的概率谓之可靠度，用Pr表示，未完成预定功能的概率谓之失效概率，用Pf表示。将影响结构功能可靠性的因素可归纳为荷载R与抗力Q两随机变量，每个随机变量可用应力、应变、变形、渗流、黏聚力、内摩擦角、重度等基本随机变量表示。

建立功能函数：

Z=g(R，Q)=R-Q

(1)

功能函数为一随机变量，表示为：

Z=g(X1，X2，…，Xn)

(2)

可靠度分析方法主要有中心点法、一次二阶矩法，二次二阶矩法，二次四阶矩、蒙特卡洛法、响应面法等。考虑到一次二阶矩法中各随机变量间是独立的正态随机变量且功能函数为多为非线性，同时计算结果相对比较精确，结合岩土工程的特点，本次土钉支护可靠度计算采用一次二阶矩法。

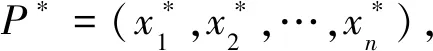
(3)

在随机变量X空间，式(3)对应的极限状态面为过P*处的极限状态面的切平面。根据统计学理论，Z的均值与标准差分别为μz和σz，分别表示为：

功能函数的均值为

(4)

标准方差为：

(5)

(6)

将式(4)、式(5)代入式(6)，得可靠度指标β：

(7)

由于上述验算点P*是假设的，故而在求取可靠度β之前先要确定P*的坐标值，然后采用迭代求解β。

P*=μXi+βσXicosθXi

(8)

3 土钉支护结构可靠度计算与分析

根据可靠性理论，结合土钉墙的岩土工程特点，土钉支护结构稳定性的可靠性理论分析可分为以下步骤：(1) 确定各基本随机变量；(2) 确定随机变量空间分布；(3) 确定土钉支护失效模式；(4) 确定极限状态建立极限状态方程；(5) 求解可靠指标。

3.1 随机变量与失效模式确定

大量实践表明土钉支护结构的稳定性与其赋存的岩土环境密切相关，与土钉自身因素的影响相对较小。而这种岩土环境的一系列变化均可引起基坑支护结构的强烈的响应，因此掌握土体工程性质变化规律，才能为土钉支护设计提供可靠的依据。在土体的诸多参数中，主要有含水率w、孔隙率、重度、液塑限、压缩系数、黏聚力以及内摩擦角等，而工程界普遍认为对土钉支护结构影响最大的是黏聚力c以及内摩擦角φ，重度γ影响甚微，同时认为黏性土的c，φ值均服从正态分布或对数正态分布，重度γ及含水率w服从正态分布，只有极少数服从威布尔分布[27]。本文通过前节试验与概率理论对西安黄土性质的关键参数随含水率变化特征作概率分析，结果见表1。

张宏刚等[28]在文中将深基坑失效模式分为两类7种分别是：坑底隆起失稳、基坑边坡失稳、坑底被动压力区踢脚失稳、坑底管涌失稳、时空效应认识不足引起的失稳、支护结构或构件失稳、支护结构踢脚失稳，此7种失效模式并不是相互独立的，而是相互耦合关联的。对于黄土地区的土钉支护主要以内部失稳、滑移失稳、倾覆失稳以及坑底土承载力不足的失效模式为主，而其余失稳模式出现相对较少，因此本文仅对黄土地区常见的四种失效模式进行可靠性分析。

表1 含水率变化时土体指标统计分析表

3.2 功能函数的建立

根据可靠性的极限状态理论，土钉支护结构失效达到概率极限状态时,令功能函数Z=R-S=0，从而建立极限状态方程，各失效模式的极限状态方程如下：

(1) 内部失稳极限状态方程

根据土钉内部失稳的机理与验算方式可知，土钉支护内部失效时的极限状态方程写为：

(9)

Tnj=πdnj∑qsiklni

(10)

在上述公式中，根据规范土钉支护内部稳定达到极限状态时Ks取1.3，式中m为滑动体内布置的土钉数；n为滑体划分的条数；wi是第i分条土的自重，滑裂面若赋存于黏土或粉土中时，按上覆土层的饱和土重度考虑；滑裂面若赋存于砂土或碎石类土中时，按上覆土层的浮重度考虑；γk取1.3；γ0是基坑侧壁重要系数；bi是第i分条宽度，m；cik、φik分别是第i分条滑裂面处土体固结不排水时的黏聚力，kPa与内摩擦角(°)的标准值；θi为第i分条滑裂面处切线与水平面的夹角；αi为土钉与水平的夹角；Li为第i分条滑裂面处弧长；lni为第j根土钉在圆弧滑裂面外穿越第i层稳定土钉内长度；Tnj为第j根土钉在圆弧滑裂面外锚固体端部与混凝土面层连接处的极限抗拔力；dnj为第j根土钉锚固体的直径，m；qsik为土钉与锚固体间粘结强度，kPa[29]。

(2) 滑移失稳极限状态方程

Z=R-S=(W+qB)Sxtanφ+cBSx-KHEax=0

(11)

根据规范土钉支护滑移失稳的极限状态时，上述公式中KH取1.40，式中各变量意义同式(1)、式(2)，其余如下：Eax为简化土墙后主动土压力水平分力；Sx为土钉间的水平间距；W为土钉支护沿基坑单位长度自重；B为土钉支护墙体平均厚度，m；c为墙底土层黏聚力标准值；q为地面均布荷载[29]。

(3) 倾覆失稳极限状态方程

(12)

根据规范土钉支护滑移失稳的极限状态时，上述公式中KQ取1.50，式中各变量意义同式(1)—式(3)，其余如下：H为基坑深度，m；H0为坑壁主动土压力区深度，m。

(4) 坑底土体承载力不足的极限状态方程

(13)

3.3 可靠指标计算

根据3.2节建立的土钉支护结构极限状态方程，采用可靠性理论，借助数学计算软件MATLAB7.0求解的可靠指标如表2所示。

土钉支护结构稳定性的可靠指标随含水率的变化如图3所示。

图3可靠指标与含水率曲线关系

(1) 在相同含水率下，土钉支护结构各失效模式的失效概率与可靠指标大小不一样；含水率在21%以下时各失效模式产生的概率相对较低。

表2 含水率变化时的各失效模式的可靠指标β计算结果

(2) 含水率达到21%左右时，土钉支护结构的失效概率开始增加，且失效的顺序性开始变的明显，失效顺序表现为：坑底土体承载力不足失效>倾覆失效>内部失效>滑移失效。当含水率增加到约30%时，土钉支护已经全部失效，且失效顺序又产生变化，表现为：坑底土体承载力不足失效>倾覆失效>内部失效>滑移失效；说明随含水率的变化土钉支护结构的失效模式是一动态变化过程。

(3) 通过数据回归分析，土钉支护结构各失稳模式的可靠指标与含水率满足对数函数关系，见式(7)。

β=-Aln(w)+B

(14)

式中：A、B均为与含水率有关的系数。

3.4 实例验证

本文通过对西安仁厚庄园项目的深基坑支护工程为例，支护工程具体设计见1.3节。经实例计算分析，认为当含水率达到21%左右时，土钉支护结构就开始逐渐发生各种模式的失效。高谦对支护工程的概率失效做了探索和研究，建议可靠度β取2.70；《建筑结构设计统一标准》对临时结构的β也建议取2.70，此时所对应的失效概率为3.5×10-3；美国LRFD对临时结构的β建议取2.50，其对应的失效概率为6.2×10-3；参考国内外关于β的建议与规定，依据式(14)中含水率与可靠指标的关系，根据可靠指标反算出含水率，计算结果见表3。

表3 不同可靠指标β对应的含水率

当土钉支护结构在工作期间如果遇到强降雨入渗或者地下管道渗水时，土钉墙可能失稳，为保证土钉墙工作的稳定性，有必要在土钉墙失效前对基坑土体中含水率变化做出预警。在综合参考前人研究成果基础上，结合黄土地区土钉支护工程成功经验，提出预警含水率，当基坑土体的含水率增加到使土钉墙不能正常工作时所具有的含水率称为报警含水率；把报警含水率所对应的可靠指标β称为临界可靠βcr，报警含水率所对应的失效概率称为临界失效概率Pcr。

根据上述定义，结合试验研究与计算分析，本文将西安仁厚庄地区土钉墙失效的报警含水率定为20.62%，临界可靠度β取3.07，对应的失效概率为5.36×10-3，即为0.536%，本文最终确定的临近可靠度和国内外规范与实践中给出的界限比较接近，说明可靠性理论分析黄土地区土钉支护的稳定性具有较好的工程实用性。在土钉支护时，可在土钉墙内布设水分传感器实现对土体含水率的实时控制，实现基坑支护稳定性的科学管控。

4 结 论

(1) 随含水率的增加，黏聚力c与内摩擦角φ均呈衰减趋势且较符合对数函数关系；含水率约在24%之前时c，φ值降幅非常显著，之后c，φ值降低趋向平缓。黏聚力降幅明显大于内摩擦角，表明含水率变化对黏聚力的弱化作用要显著的强于对内摩擦角的弱化，也说明了黏聚力对水的敏感性强于内摩擦角。

(2) 在室内试验基础上，通过可靠性理论分析，得出土体含水率增至21%左右时，土钉支护结构开始产生失效且各失效模式产生时具有显著的顺序性，分别为坑底土体承载力不足失效、倾覆失效、内部失效、滑移失效；当含水率增至约30%时，土钉支护全部失效，且失效顺序又产生新的变化；最后得出了可靠指标与含水率的函数关系β=-Aln(w)+B。

(3) 通过分析和实例验证提出了报警含水率和临界可靠度的定义，并将西安地区土钉墙失效的报警含水率定为20.62%，对应的临界可靠度β为3.07，失效概率为5.36×10-3。