基于统计模型的高心墙堆石坝沉降变形研究

张 艺，迟世春，周雄雄

(1.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 建设工程学部 水利工程学院工程抗震研究所， 辽宁 大连 116024)

土石坝是使用最广泛的坝型，中国的百米级土石坝工程从鲁布革土质心墙堆石坝开始，1980年以前中国百级的土石坝仅有3座[1]，随后一批具有代表性的工程相继完成，主要有坝高154 m的小浪底斜心墙堆石坝，233 m的水布垭面板坝，261.5 m的糯扎渡心墙堆石等等；目前，我国高土石坝的发展已向300 m级高度研发和建设，在建314 m高的双江口心墙堆石坝将成为世界上最高的土质心墙堆石坝[2-3]。

随着大坝的数量和高度不断增加，土石坝工程的安全问题也愈发重要，除地震破坏和溃坝失稳等问题，坝体内部水压力过大、后期流变和湿化[4]导致的变形也是不可忽略的安全问题。土石料作为典型的岩土材料不仅有较强的非线性，而且具有蠕变特性，坝体在竣工蓄水后还将持续发生变形，很多学者对此做了相应研究[5-7]。为及时掌握土石坝运行状况，通常在土石坝内部和表面设置相应安全监测点，实时全面监控，并对不同部位的观测点进行数据整理和分析，直观了解大坝的运行状态，进一步掌握土石坝的工作规律，并及时发现存在的隐患，从而保证大坝运行安全。

大坝变形研究的主要方法有回归分析、有限元数值分析法[8]、时间序列分析法[9]、频谱分析法[10]、小波分析法[11]和时空自回归[12]等等。我国的大坝监测工作始于20世纪50年代初期，80年代开始利用统计方法分析原型观测资料。经过前人的不断研究总结，认为统计回归分析模型具有力学解释清晰、适应性广、可靠度高等优点，吴中如[13]将分析统计模型归纳为3种，分别为统计模型、确定性模型或混合模型，并讨论了土石坝沉降影响因子的选择和表达形式。然而，单独测点的沉降模型不能描绘大坝的整体形态，对不同因素耦合影响也无法清晰描述。本文分别选取大坝心墙、下游堆石体和表面的测点，使用统一沉降模型解释沉降中主要因素的共同影响。

本文利用原型观测资料，分析土石坝影响沉降的因素与沉降量间的关系，讨论在沉降模型中上游水位、填筑高度和时效因素等影响，最后采用回归分析方法对某高心墙堆石坝典型剖面上的测点观测数据进行拟合，得到沉降模型，探讨各影响分量与沉降量的占比，并实现对该土石坝沉降的预测。

1 统计模型的建立

在原型观测中，一般来说沉降值最大，因此变形监测统计模型都以沉降模型为主。沉降受诸多因素影响，如地形地质条件、水文气候条件、施工工序与质量等，使得大坝在建设和运行中的情况较为复杂，大坝的沉降规律难以简单描述。在统计模型中较难全部考虑上述因素，本文就填筑分量、蓄水分量和时效分量做讨论。

1.1 模型的选择

1.2.2 水压分量

沉降模型中共有八个参数，分别为a1，a2，a3，b1，b2，b3，c1，c2分别为填筑、水压和时效分量的回归系数。

根据土石坝变形机理和以上分量的综合考虑，选择填筑、蓄水和流变这三个主要的影响因素建立沉降模型：

δ=δd+δh+δθ

(1)

式中：δ为沉降总量；δd为填筑分量；δh为水压分量；δθ为时效分量。

素养考查分析：这是一道数学应用题，综合考查了组合学、概率论、导函数、函数的单调性、函数的最值、数学期望等基本知识，以及运用组合公式、求函数的导函数，判断函数单调性、计算数学期望等基本技能．

1.2 模型因子的选择

其中：δH为水压分量；Hi为自观测日上游水位变化；bi为水位回归系数。

除上述各因素外，还需要综合考虑电动机运行的可靠性，备品备件的通用性、安装维修的难易程度、以及产品价格、运行费用和维修费用等各项经济指标，达到安全运行和节约能源的目的.

在施工期因为坝体填筑高度不断增加，自重引起的有效应力显著增大，导致填筑初期孔隙体积较大的部位孔隙迅速缩小、强度低于挤压应力的颗粒发生破碎、颗粒间相互滑移、重排产生瞬时变形，这一过程使得沉降快速增大。沈长松根据坝工理论和以往的经验[14]将填筑分量表示为：

(2)

其中：δd为填筑分量；hd为测点以上填筑增加高度；ai为填筑回归系数。

选择的模型必须满足大坝沉降的整体变形规律，反映沉降过程特性，较好拟合沉降过程中的数值，同时要注意模型的实用性。

在上游水位不断上升过程中，水压力、浮力和上游堆石料的湿化变形将影响坝体的沉降，坝体的沉降与上游水深变化的次方关系有关，吴中如等[13]总结水压分量可以表示为：

(3)

1.2.1 填筑分量

1.2.3 时效分量

计算完毕后，比较竣工和设计标高差异值。其中在公式（2）中的可以直接作为实际施工立模标高。正向分析法主要是按照实际施工的步骤顺序进行桥梁施工数据的分析测算，合理解决了传统的倒装分析法不可避免的桥梁连续施工混凝土收缩不变的计算问题[3]。假设在实际计算过程中，桥梁施工单位在第一阶段应力并没有通过，也可以及时进行调整。此外，正向分析法可以充分考虑设计资料和相应施工方案，对桥梁结构工程、施工工作以及后续的工程监管融为一体，保证监管工作的现实性和针对性。

堆石体由大量堆石颗粒组成，具有较明显的流变特性，已有学者针对蠕变模型进行相关研究[15-17]。刘正云等[18]将由固结引起的时效分量归纳为直线形式、双曲函数形式、对数函数形式、指数形式、复合函数形式，具体表达如下：

(4～9)

通过分析坝顶表面视准线监测数据，经过拟合分析，将时效分量选为双曲线形式。沉降模型可表达为：

鉴于东海2号机组于1978年投运，原子能电力已于2017年11月向规制委提交延寿申请。要想让这份申请获得批准，该公司必须在2018年11月底这一法定截止日之前获得规制委对下述两份计划的批准：安全强化措施详细执行计划和延寿改造详细计划。

(10)

本文研究参考的大坝位于云南地区，常年气候温度适宜，可忽略温度分量的影响。坝体上下游堆石料和反滤料施工时不受降雨影响，心墙在旱季施工避免防渗料经水，因此也不考虑降雨带来的沉降变形。

大坝填筑量大，施工时间长，在施工期包含两次蓄水过程，所以施工阶段沉降同时包含填筑分量、水压分量和时效分量，运行阶段沉降主要受水位和流变影响。

再看欧阳修。欧阳修早年也是范仲淹的崇信者，曾为范仲淹而写了《与高司谏书》那样笔锋锐利的作品，也曾经为了范仲淹而与丈人胥偃产生裂痕。据《长编》记载：

我院体育教学一直紧随素质教育的步伐改革创新，在实践中探索出符合我院校情，学情的体育教学模式。从2002年陆续与社会企业场馆达成合作开始，拉开了我院体育教学改革的序幕，像游泳、保龄球、乒乓球、网球等运动项目在体育课中开设，受到广大学生的欢迎和认可，学习热情空前高涨。至此，我院的体育教学不再以田径和三大球教学为主，而是以田径和三大球为基础，培训师资，逐年增设新的运动项目。轮滑就是在这样的背景下引入了我院的体育教学。

2 工程应用

2.1 工程概况

该土石坝位于云南省境内，是澜沧江下游的核心水电工程。最大坝高为261.5 m，拦河大坝为中央直立心墙堆石坝，心墙料采用掺砾料，心墙两侧设置反滤层，坝体外侧为堆石体坝壳。坝顶长为630 m，宽度为18 m，上游坝坡坡度为1∶1.9，下游坝坡坡度为1∶1.8。

心墙于2008年11月开始填筑，2012年5月31日坝体填筑高程达到802.00 m，开始全断面填筑，2012年底前坝体填筑完成。大坝蓄水一共分三个阶段，前两个阶段都在填筑期，第一阶段2011年11月—2012年2月，上游水位升至高程为705 m，第二阶段2012年4月—2012年8月，上游水位升至高程为765 m；第三阶段2013年7月开始，运行期水位最高升至812.09 m，第三次蓄水后水位周期性上升下降。

针对大坝最大断面设置变形监测仪器，心墙571 m高程往上每3 m设置一个电磁沉降环测点，上下游均在高程660 m、701 m、738 m和780 m处设置数量不等的沉降仪，在大坝上下游表面同内部相同高程处设置视准线表观点监测，具体分布如图1所示。

2.2 沉降模型拟合与结果分析

在沉降模型理论建立的基础上，对影响因子的显著性进行检验，检验结果为各影响分量与沉降的相关系数基本在0.6以上，相关性较为明显，说明选取的影响因子合理。经过数据预处理后，利用多元非线性回归的数学思想，基于MATLAB编程的方法建立关于大坝主要断面测点的沉降模型。

假设时钟信号在参考时间0时刻变化，那么时钟信号在触发器i和j上改变的时间分别是xi和xj.为了满足建立时间和保持时间，因此需满足以下公式：

第一，企业对财务人员进行意识教育。大数据时代的来临为我们提供了许多的便利，同时也带来了许多的潜在性和不确定性的风险。邀请专家对于最新的政策进行解读，让会计人员在理解上减少偏差和失误的可能，同时通过对于政策的解读，让财务人员明确政策颁布后的责任主体是谁，让财务人员认识到会计舞弊或违法操作(故意泄露数据等)等行为的严重后果。例如2018年新颁布的俗称“会计人员‘黑名单’制度”，企业可通过一系列系统的培训，让企业中的会计从业人员对于会计职业中的风险有一个清晰的认识，了解其中危害，从自身就有一个自律的意识。

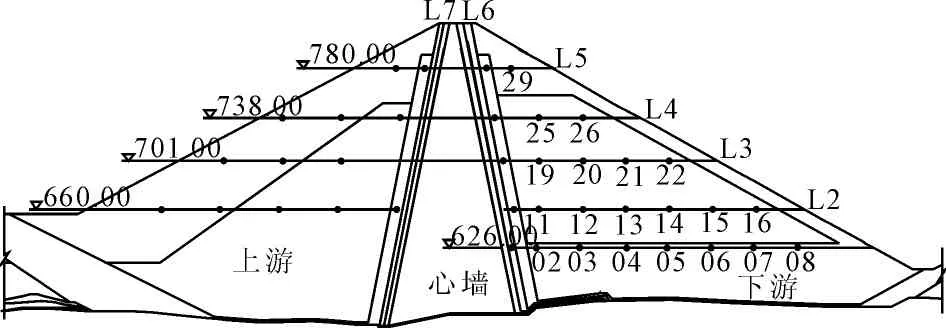
图1最大断面监测仪器布置示意图

2.2.1 内部沉降模型

对于文科生而言，汉语言吸引力比较强。虽然汉语言专业惠及范围广，但因主要以文科生为主，所以汉语言文学专业教学中，文科生是教学的主要对象。当然，有的学生考上大学后，开始学习汉语言文学专业，这也充分体现了专业的魅力。因而语言应用意境分析备受关注。

选择大坝下游内部626 m高程处测点DB-C-V-02，对时间2010年1月8日—2013年10月18日280个数据进行分析，此时间段包含填筑和蓄水过程，利用已得出沉降模型对2013年10月23日—2015年5月21日83个数据进行预测。另选下游内部738 m高程处测点DB-C-V-26，对时间2011年8月7日—2013年10月18日共215个数据进行分析，此时间段包含填筑和蓄水过程，利用已得出沉降模型对2013年10月23日—2015年5月21日83个数据进行预测。

本系统基于单总线EEPROM芯片DS2431设计eID方式的电子标签，具有体积小、触点少、可实时读写等优点。通过在光纤连接器上安装eID标签，在光纤熔配一体化托盘（以下简称光纤托盘）的活动连接器上安装eID标签插座，光纤托盘内部布放存有内部光纤连接信息的数据采集电路板，实现了对光纤托盘每路活动连接器两端光纤信息的数据采集，从而实现了ODN的数字化和智能化管理。

选择大坝心墙内部740 m高程处测点DB-C-SR-52，对时间2011年8月20日—2012年8月28日50个数据进行分析，此时间段只有填筑过程，利用已得出沉降模型对2012年9月4日—2012年10月24日10个数据进行预测。另选心墙内部790 m高程处测点DB-C-SR-66，对时间2012年8月3日—2013年8月3日共104个数据进行分析，此时间段包含填筑和蓄水过程，利用已得出沉降模型对2013年8月4—2014年1月10日87个数据进行预测。

以上测点多元回归分析拟合结果见表1，沉降模型的拟合和预测效果见图2—图5。

表1 大坝内部沉降模型计算结果

图2 下游堆石体DB-C-V-02测点沉降拟合预测图

图3 下游堆石体DB-C-V-26测点沉降拟合预测图

图4 心墙DB-C-SR-52测点沉降拟合预测图

图5心墙DB-C-SR-66测点沉降拟合预测效图

2.2.2 表面沉降模型

选择大坝下游701 m高程处L3视准线，对时间2011年5月11日—2014年8月14日256个数据进行分析，此时间段包含填筑和蓄水过程，利用已得出沉降模型对2014年8月20日—2015年5月15日42个数据进行预测。坝顶选择L6视准线，对时间2013年8月17日—2014年8月14日共176个数据进行分析，此时间段填筑已经结束，只包含蓄水过程，利用已得出沉降模型对2014年8月20日—2015年5月15日42个数据进行预测。

L3视准线共有9个监测点，L6视准线共有13个监测点，均选取其中最大沉降量的两个测点进行多元回归分析，拟合结果见表2，沉降模型的拟合和预测效果见图6—图10。

第三，形成了一些比较有效的课堂规范，但也有一些课堂规范阻碍了学生的自由发展.张老师经过多年的教学实践，形成了自己的一套课堂教学规范.如一个学生在回答问题时，要求其他学生保持安静，待这位学生讲完后再发表意见.这样的课堂规范，有利于养成学生学会倾听，并对他人的观点进行思考的习惯.但是还有一些课堂规范不利于学生的自由发展，如要求学生想到解答方法或获得答案后不能随便发言，等老师点名后才可以回答；再如，要求学生统一解题思路后，再动手做题.

图6下游堆石体L3-TP-05测点沉降拟合预测图

表2 大坝表面沉降模型计算结果

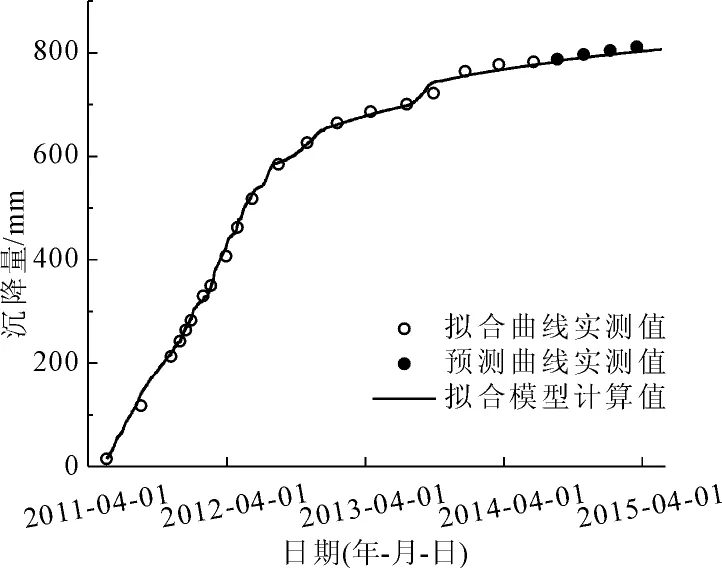
图7 下游堆石体L3-TP-06测点沉降拟合预测图

图8 坝顶L6-TP-07测点沉降拟合预测图

图9坝顶L6-TP-08测点沉降拟合预测图

2.2.3 沉降模型预测结果分析

沉降模型的回归分析结果见表3，由表3数据可知，表面沉降预测平均相对误差最大为2.18%，内部沉降预测平均相对误差最大为1.30%，复相关系数都在0.9以上，说明沉降模型预测效果较好，贴近实际变化。证明通过考虑了填筑分量、水压分量和时效分量耦合的影响后，所建立的沉降模型精度高，拟合效果好，实用性强。

2.3 沉降模型分离结果与分析

根据得出的沉降模型可以定量分离和分析填筑、水压和时效三方面的分量， 进一步分析这些因素变化对沉降的影响，选取以上测点利用拟合模型结果进行统计，计算分量与沉降值的比例数值，结果见表4。

直流电动机实质上是自控变频电动机，而广义直流电动机是自控变频电动机系统。对于电机本体，式(1)中的sinδ可以有控制地取值，具有如此关系的电磁转矩方可实施人为控制。

表3 坝体预测结果

从分离结果可知，各测点的沉降量组成分量与测点位置有明显的相关性。

填筑分量在填筑过程中影响较大，内部点相较表面点更为敏感，内部测点占比均超过50%，表面也高达30%以上；同一高程填筑占比相似，说明大坝沉降均匀；随高程增大沉降占比减小。水压分量均不同程度的选入沉降模型，但对心墙坝顶处影响较大，而下游堆石体测点受水位影响相对较小，一般不超过10%；对于高程740 m心墙测点DB-C-SR-52观测时段，坝体初蓄水至700 m，可认为水压变化在此时间段无影响。由时效分量统计结果可知，时效分量对沉降影响显著，大坝表面视准线观测点时效分量比例高达60%以上，高程较小的下游堆石体占比也大于20%，说明土石坝流变特性不可忽略，坝顶高程处视准线L6在观测时段已完成填筑的坝顶，时效分量高于80%，另外心墙测点DB-C-SR-52较测点DB-C-SR-66时效分量占比小，是因为观测时间在填筑期内，观测时间较短，故填筑分量大时效分量小，而测点DB-C-SR-66经历填筑和运行阶段，流变时长较长，时效分量占比变大。

分离结果基本符合大坝沉降规律，说明本文沉降模型对大坝沉降的拟合、预测和分离是合理的。

3 结 论

本文结合高心墙堆石坝实际工程建立大坝沉降的统计模型，确定了坝体沉降变化的主要影响因子，在此基础上建立满足该大坝沉降规律的统计模型，得到结论：

(1) 应用多元回归分析方法，建立的沉降监控模型实用性强，拟合效果佳，在利用实测数据修正的情况下，可以利用沉降模型做出有效预测。

表4 大坝沉降拟合与分离结果

(2) 整理分析拟合结果，可知大坝沉降值在填筑时期主要受填筑因素影响，在运行期间主要受时效因素影响。与观测值对比，可以认为回归模型可以较好地计算填筑、水位、时效因素引起的变形。