液化天然气饱和单液滴蒸发模型及其吹拂效应的影响
邓佳佳, 许 健, 卢金树, 石墩章
(1. 浙江海洋大学 港航与交通运输工程学院, 浙江 舟山, 316022; 2. 舟山博睿船舶科技开发有限公司, 浙江 舟山, 316000)
储运天然气最安全、经济的方式是将其转化为液化天然气(LNG).在LNG液舱投产准备中,约有一半的事故发生在预冷过程[1-2].液舱预冷是将制冷剂雾化喷入、利用制冷剂液滴相变而实现的[3-4].为防止结冰堵塞,液舱预冷前需将舱内气体置换为液滴蒸气.
目前,因实验设备昂贵且理论研究难度较大,液舱预冷过程的实验和理论研究还少见报道,而且单液滴在其蒸气中的蒸发理论模型欠缺,又制约了其数值模拟的发展.液体与其蒸气的传热传质过程模拟通常采用Lee模型[5-6].Lee模型适用于压力恒定且温度接近于饱和温度的传热过程模拟,如水沸腾[7-8].LNG液舱预冷的初始温度远高于其饱和温度,传质非常剧烈[9],界面处蒸气喷出速度较大,对传热具有阻碍作用,即形成吹拂效应[10];而且液舱预冷过程中的舱内温度变化较大,吹拂效应的影响也不断变化,但Lee模型未考虑吹拂效应及其变化的影响,因此,本文基于液滴界面能量守恒原理建立了LNG饱和单液滴在其蒸气中的蒸发模型,分析了吹拂效应对液滴蒸发的影响,以期为完善LNG液滴蒸发模型及保障LNG液舱操作安全提供参考.
1 模型及验证
1.1 模型假设
在LNG液舱预冷过程中,喷淋的LNG液滴是饱和液滴,因而其吸收的热量完全用于液相蒸发.LNG单液滴在其蒸气中的蒸发过程非常复杂,为了简化模型,本文进行如下假设:
(1) 蒸发过程中的液滴呈球形,且气相流场结构为轴对称,采用二维轴对称坐标系;
(2) 采用液态甲烷液滴和气相甲烷作为LNG模型工质;
(3) 气-液界面及液滴内部的温度均为饱和温度,气-液界面的相变符合准稳态假设,且相变只发生在气-液界面;
(4) 因为LNG液滴为饱和液滴且处于稳态蒸发阶段[11],液滴内部的运动对液滴传热传质的影响很小,所以忽略液滴内部运动的影响;
(5) 忽略辐射热的影响.
1.2 数学模型
基于以上假设和液滴界面能量守恒原理,采用计算流体动力学方法建立单液滴的蒸发模型.采用稳态二维轴对称坐标系,其模型方程包含连续性方程、动量方程、能量方程和湍流模型[12].
连续性方程为
(1)
式中:x为轴向坐标;r为径向坐标;vx为轴向速度;vr为径向速度;ρ为蒸气密度.
动量守恒方程为
式中:p为压力;μ为黏度;v为速度矢量.
能量守恒方程为
(4)

加入组分方程后,该模型可用于液滴在混合介质中的蒸发模拟.组分扩散方程为
(5)
式中:wi为i相的质量分数;Ji为i相的扩散通量.
由于液滴界面边界层对液滴蒸发的影响非常大,为准确模拟液滴界面边界层,本文采用SSTk-ω湍流模型[13].其中,将近壁区间与远场区间分开处理,以准确模拟近壁区间层流边界层的流体流动,其方程为
式中:k为湍动能;ω为比耗散率;Gk为平均速度梯度湍动能生成项;Gω为比耗散率的生成项;Γk、Γω分别为湍动能和比耗散率的有效扩散系数;Yk、Yω分别为湍动能和比耗散率的湍流耗散量;Sk、Sω分别为湍动能和比耗散率的源项;Dω为正交发散项.
气-液界面处气相传递给液相的热量等于气-液界面处液体相变所需相变潜热,即气-液界面的边界条件为
(8)
式中:v2为气-液界面处蒸发蒸气的速度;q为气-液界面处气相传递给液相的热流密度;Q为液相的蒸发潜热.
选择理想气体模型来计算蒸气的密度,即
(9)
式中:R为普适气体常数;Mw为蒸气的相对分子质量;pop为操作压力;p1为相对压力.
1.3 模拟条件及网格
根据静止液滴与运动液滴蒸发的流场特性的不同,分别采用不同的网格.具体模型及网格如图1所示. 其中:边界条件分别为进口温度Tr=110 K,出口温度Tout=300 K.表1列出了所用介质的热物理性能参数.其中:cp为定压比热容;λ为导热系数;各参数的分段线性来源于软件数据库[14].

介质ρ/(g·cm-3) cp/[J·(kg·K)-1]μ/[g·(m·s)-1]λ/[W·(m·K)-1]Q/(kJ·kg-1)饱和LNG----511.15天然气理想气体线性分段线性分段线性-葵烷液滴0.603---293.31葵烷蒸气理想气体线性0.540.147-
1.4 模型验证
本文利用上述模型对粒径d=2 mm的葵烷液滴在1 000 K高温空气中的蒸发实验[15]进行模拟.为了与实验数据进行对比,对计算结果进行后处理.以液滴粒径作为因变量,采用2次抛物线将计算结果拟合而得到质量蒸发速率的函数f(d),拟合结果如图2(a)所示.进一步采用下式对拟合函数进行转换:
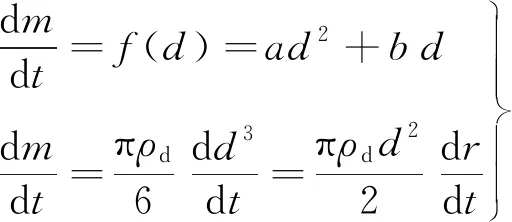
(10)
得到不同粒径的液滴完全蒸发所需时间为
(11)
式中:m为液滴质量;ρd液滴密度;a、b均为拟合函数的系数.

图2 计算结果与实验结果的对比Fig.2 Calculation results versus experimental results
计算所得液滴粒径的平方与液滴蒸发时间的关系,以及液滴温度达到饱和温度后的实验数据[14]如图2(b)所示.由图2(b)可见,模型的计算值与实验数据吻合较好.
2 结果与分析
2.1 静止LNG液滴的蒸发特性
2.1.1气-液相温差的影响 图3所示为不同的气-液相的温差ΔT下d=1 mm的静止LNG液滴在蒸发过程的温度边界层厚度δT以及界面换热量对比.由图3可知:在液滴粒径相同的情况下,随着ΔT增加,蒸发产生的吹拂效应使得温度边界层变厚,有、无蒸发时温度边界层厚度之比ζ呈线性增长,其变化曲线的斜率为 5.16×10-3K-1;当ΔT<165 K时,ζ<2.00,两者的换热量非常接近,有、无蒸发时的液滴界面换热量之比β=0.982,表明吹拂效应(1-β)仅为 2.80%,即吹拂效应的影响较小;当ΔT>165 K时,随着ΔT逐渐增大,两者的液滴界面换热量差距越来越大,其β值随着温差增加而呈现出线性降低,其变化曲线的斜率约 -1.03×10-3K-1,当ΔT=490 K时,吹拂效应达到 35.20%.

图3 不同温差下静止液滴的蒸发特性对比Fig.3 The evaporated characteristic comparison of static droplets versus temperature differences
2.1.2液滴粒径的影响 图4所示为不同粒径的静止LNG液滴在300 K的蒸气中,当考虑、未考虑液滴蒸发时蒸发温度边界层厚度及液滴界面换热量的对比.由图4可以看出:在温差保持不变、液滴粒径逐渐增大的情况下,考虑及未考虑液滴蒸发过程的液滴界面换热量及温度边界层厚度均呈线性增长;其ζ基本保持不变,且ζ=2.34;另外,液滴界面换热量的差别并不大,其β值约为 0.955,吹拂效应仅为 4.50%.
综上所述,在考虑液滴蒸发的情况下,由于液滴蒸发的蒸气运动方向与传热方向相反,所以阻碍了传热,且使得温度边界层变厚.吹拂效应对温度边界层厚度的影响随着温差增大而呈线性增长,但随着液滴粒径的增加而几乎保持不变.吹拂效应对液滴界面换热量的影响随着温差增大而呈现出分段变化特征,当ΔT处于0~165 K时,吹拂效应对传热及传质的影响很小,仅为 2.76%;当ΔT处于165~490 K时,吹拂效应的影响逐渐增大,吹拂效应最大可达 35.20%;随着液滴粒径增大,吹拂效应对液滴界面换热量的影响不大,仅为 4.50%.

图4 不同液滴粒径时的温度边界层厚度及界面换热量Fig.4 Temperature boundary layer and blowing effect versus particle sizes
2.2 运动LNG液滴的蒸发特性
通过对静止LNG液滴的蒸发特性分析可知,气-液相温差的影响明显大于液滴粒径的影响,因此,本文在分析运动LNG液滴的蒸发特性时,重点考虑气-液相温差ΔT及相对速度v的影响.由于运动液滴蒸发过程中,温度边界层沿液滴圆周方向的厚度分布不均匀,所以只采用最薄边界层厚度进行分析.
2.2.1气-液相温差的影响 图5所示为不同的气-液相温差、v=10 m/s下,d=1 mm的液滴在考虑和未考虑液滴蒸发时的温度边界层厚度和液滴界面换热量及其比值.由图5可以看出:随着ΔT增加,温度边界层厚度及液滴界面换热量均增大;ζ值呈线性增长,其变化曲线的斜率为 4.72×10-4K-1;β值随着ΔT增加也呈现出分段变化趋势,当ΔT=40 K 时,β=0.974,吹拂效应的影响非常小,仅为 2.60%;当ΔT≥40 K时,其β值呈现出线性减小的变化趋势,其变化曲线的斜率约为 -1.99×10-3K-1,当ΔT=190 K时,吹拂效应使得液滴界面换热量降低了 32.7%.

图5 不同温差下运动液滴的温度边界层厚度及界面换热量Fig.5 Temperature boundary layer thickness and heat transfer rate versus temperature differences of moving droplets
2.2.2相对速度的影响 图6所示为不同的相对速度v下,d=1 mm的运动液滴在气相温度为200 K、考虑和不考虑蒸发时温度边界层厚度及界面换热量及其比值的对比.由图6可以看出:随着v增加,温度边界厚度逐渐降低,液滴界面换热量逐渐增加,ζ呈现出小幅增长的变化趋势,其变化曲线的斜率为 3.50×10-3K-1;β值也随着v增加而呈现出线性增长,其变化曲线的斜率为 8.46×10-3K-1;当v=18 m/s时,β=0.949,吹拂效应的影响可以忽略.

图6 运动液滴在不同相对速度下的温度边界层厚度及界面换热量Fig.6 Temperature boundary thickness and heat transfer rate versus relative speeds of moving droplets
3 结论
(1) 基于液滴界面能量守恒原理所建适用于LNG单液滴在其蒸气中的蒸发模型的计算结果与实验结果较吻合.
(2) 在静止LNG液滴蒸发过程中,由于蒸发产生的吹拂效应而使得温度边界层变厚;随着温差增大,吹拂效应对温度边界层厚度的影响呈线性增长,而液滴粒径对其影响不大.随着温差增加,吹拂效应对液滴界面换热量的影响呈现出分段变化特征,且分段点为165 K;随着液滴粒径增大,吹拂效应对液滴界面换热量的影响保持恒定且很小.
(3) 在运动LNG液滴蒸发过程中,随着温差及运动速度增加,考虑、未考虑液滴蒸发时温度边界层厚度之比呈现出微弱的线性增长趋势;随着温差增加,吹拂效应对液滴界面换热量的影响呈现出分段变化特征,且分段点为40 K;随着相对速度增加,液滴界面换热量增大,吹拂效应对液滴蒸发的影响逐渐减小,当相对速度大于18 m/s时其影响可以忽略.
(4) 运动使得吹拂效应对液滴界面传热量的影响的分段点提前,从165 K提前至40 K,并且使其线性减小段的斜率增加.

