一种几何VOF方法在液舱晃荡流动模拟中的应用

李金龙， 尤云祥， 陈 科

(上海交通大学 海洋工程国家重点实验室； 高新船舶与深海开发装备协同创新中心， 上海 200240)

浮式天然气生产储卸船通过低温的方式将在海上开采到的天然气储存在船体内部液舱.这些液舱没有装载率的限制，部分装载的液舱在海洋波浪的激励下产生晃荡，影响船舶的运动、稳性及其结构安全，是工程上关注的热点问题[1].近年来，随着计算机技术的发展与进步，计算流体力学(CFD)变得越来越流行.CFD 的两相流求解器在模拟液舱晃荡流动时遇到的主要问题之一是如何处理自由液面的不连续性以及如何表达物理量在自由液面处的阶跃[2].确定自由液面位置主要有界面追踪和界面捕捉两类方法[3].界面追踪方法追踪相界面的运动，例如 MAC (Marker-and-Cell)[4]、FT (Front-Tracking)[5]、ALE (Arbitrary Lagrangian-Eulerian)[6]以及σ-transformation 等方法[7].界面捕捉方法基于固定的Euler网格，借助一个标量场分布捕捉相界面的位置，允许较大的相界面变形、破碎以及合并等复杂拓扑变化.典型的界面捕捉方法包括 VOF和LS(Level Set)方法[3].VOF 方法采用体积分数率的分布捕捉两相界面的位置，且能保证质量守恒，尤其适用于液舱晃荡类封闭空间内的液体流动模拟计算.该方法又可以分为代数VOF和几何VOF方法[2].代数VOF方法适用于任意三维网格，利用高精度格式和压缩差分格式求解体积分数率输运方程，以保证体积分数率的有界性，例如 OpenFOAM 中的 MULES (Multi-dimensional Universal Limi-ter with Explicit Solution).几何 VOF 方法需进行界面重构，并计算网格单元和相界面的交线，再用重构出的几何相界面更新体积分数率的分布.例如:SOLA (Solution Algorithm)-VOF 应用贡献者-接受者通量近似的方法重构相界面形状[8]；SLIC (Simple Line Interface Calculation)[9]和 PLIC (Piecewise Linear Interface Calculation)[10]通过求取当地相界面法向量重构几何相界面.采用这些界面重构方法都能获得明锐(相界面不连续性明显)的两相界面，但是这些方法通常仅适用于结构化网格，当推广到三维网格时会引起复杂的几何运算，而推广到三维非结构化网格时则遇到了困难.最近被提出的isoAdvector方法构造了isoface重构几何界面，并根据 isoface 的运动更新体积分数率的分布.相对于代数 VOF 方法而言，isoAdvector 方法能捕捉更为明锐和准确的相界面[2]，可适用于三维任意多面体网格.

本文采用动网格技术处理液舱运动，且避免引入液舱平移和旋转惯性力求解非惯性坐标系下的动量方程，避免处理惯性力涉及的导数[11-12].采用isoAdvector 方法捕捉自由液面并考虑动网格的影响，引入了运动通量修正，提出了面-界面交线运动修正.采用一种近似公式，根据网格单元面上的运动通量重构出网格单元体心的刚体运动速度.基于不同的 VOF 方法对受迫非共振晃荡、受迫共振晃荡以及单次冲击波面进行了模拟，并将模拟结果与试验结果以及解析解进行了比较.此外，提出了新的估计两相界面厚度的方法.

1 数学模型

基于开源平台 OpenFOAM，采用有限体积法离散 RANS (Reynolds-averaged Navier-Stokes) 方程.

1.1 控制方程

两相流被视为一种单一的连续介质，可采用一套控制方程来求解连续介质的流动.连续方程和动量方程采用张量表达：

(1)

(2)

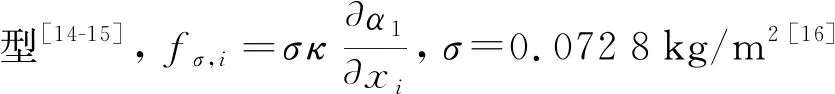
式(2)的右端项涉及变换

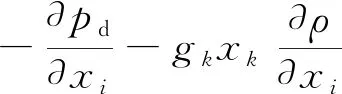
(3)

gi=0

1.2 几何 VOF 方法——isoAdvector

isoAdvector 方法分为两个步骤：① 根据当前的体积分数率场，在每一个界面网格单元(该单元的体积分数率介于0和1之间)重构出一系列的几何平面(isoface)，每一个 isoface将其所在的界面单元分割为两个子单元，这两个子单元分别被两相流体填充，其体积比和该网格单元的体积分数率一致.isoface的集合可以视为两相界面的一种表达，但该集合所表示的几何面在各个网格单元交界处可能存在不连续性[2].② 利用速度场预测这些 isofaces 的运动，从而更新体积分数率场.此更新操作不涉及求解线性代数方程组的问题，避免了选取高精度和压缩差分格式.由于本文利用动网格技术来处理液舱的运动，所以需要对 isoAdvector 方法进行下列两个方面的修正.

首先通过对体积分数率更新公式的重新推导，引入第一个修正.定义相指示函数[2]

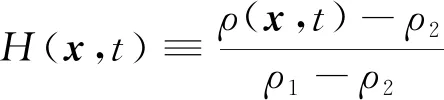
(4)

式中：x是空间位置坐标；ρ1和ρ2分别为液相和气相的密度.如果x=(xi,xj,xk)处于液相，则H=1；如果x处于气相，则H=0.

连续介质的质量守恒方程为

(5)

式中：u是连续介质的流速.设V是控制体体积，∂V是控制体的边界，n是边界的单位外法向量.对式(5)关于控制体进行体积分得

(6)

分别采用雷诺输运定理、散度定理对式(6)的第1和2项进行变换得

(7)

式中：ub是控制体边界的移动速度；dS是控制体面上积分微元.将式(4)代入式(7)得

(8)

式中：Fj为单元面；j为单元面的索引；B为单元面总数.液相体积分数率定义为

(9)

将式(9)代入式(8)，并在等式两端对时间积分，得到在该控制体处体积分数率的更新公式：

α1(t+Δt)=α1(t)-

(10)

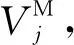
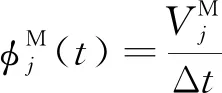
(11)

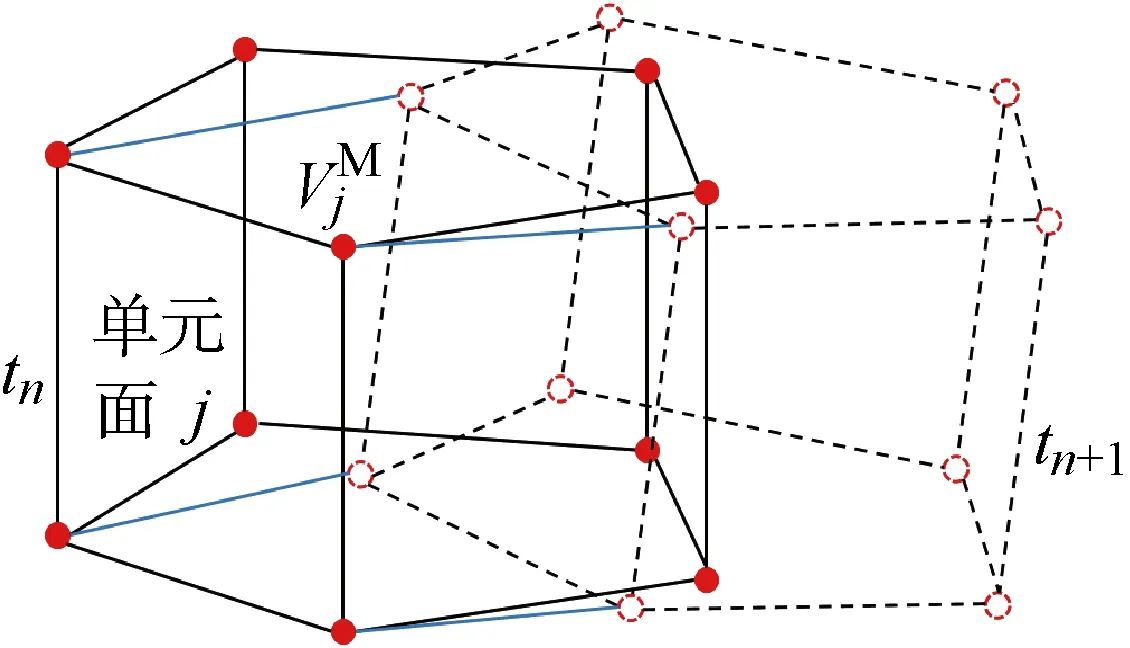
图1 网格的刚体运动和单元面扫过的体积Fig.1 The solid-body motion of the mesh and the volume swept by a cell face

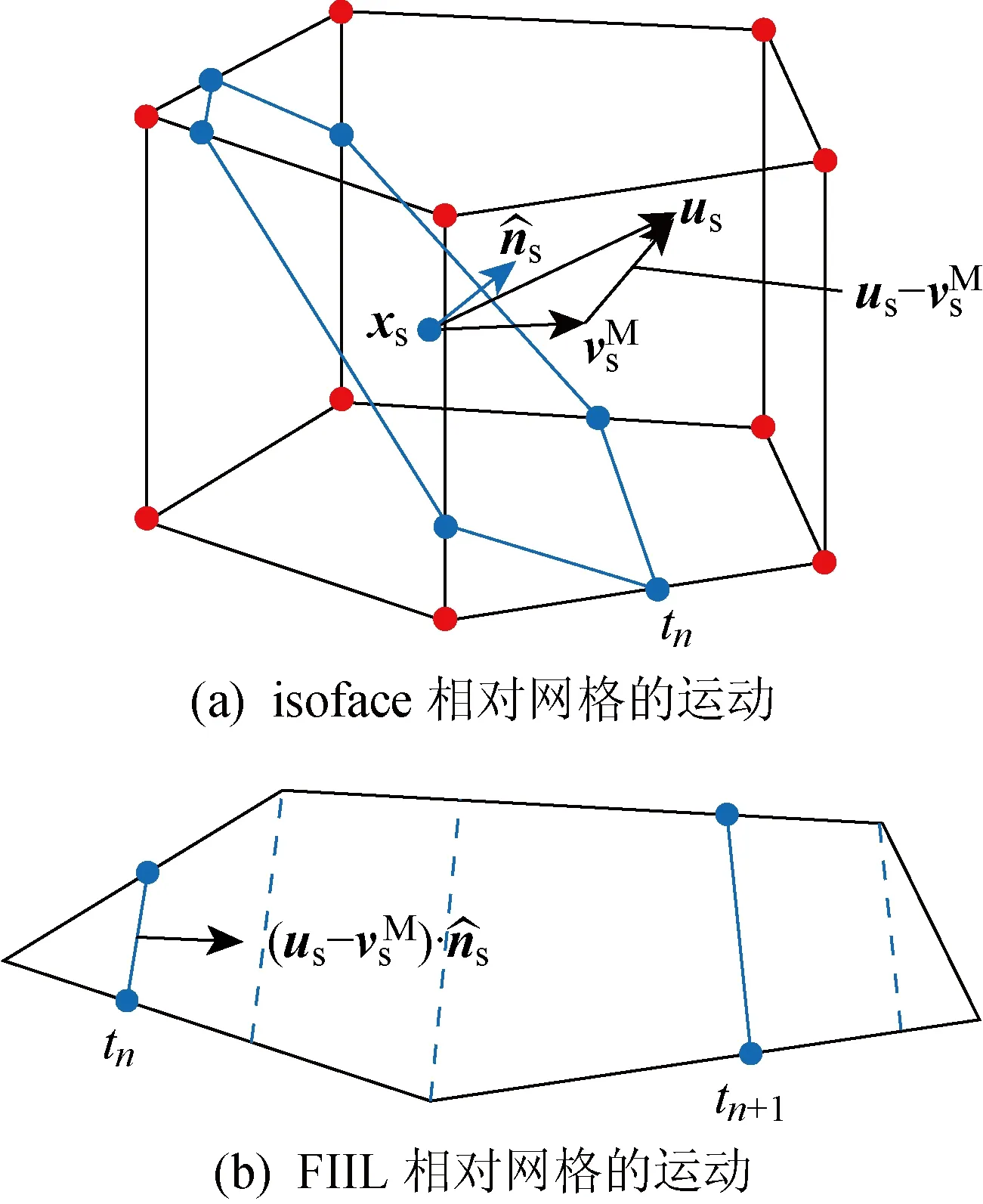
图2 面-界面交线运动修正Fig.2 The moving velocity corrections for face-interface intersection line

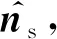
对于任意一个网格单元i，有如下等式近似成立：

(12)

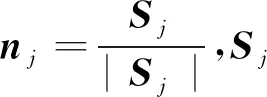
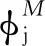
下文中，经过运动通量修正和面-界面运动修正的 isoAdvector 方法称为 isoAdvector-c2，仅有运动通量修正的 isoAdvector 方法称为isoAdvector-c1.和几何 VOF 方法不同，代数 VOF 方法不涉及任何关于几何体的操作，而是求解关于体积分数率的输运方程[13].

1.3 界面厚度估计

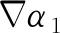
1.4 数值模拟的相关设置

由于计算域是封闭的空间，所有的边界都是移动的壁面.采用浮力修正的k-ωSST 湍流模型[17]模拟湍流的影响.用 Crank-Nicolson 格式离散瞬态项，用高精度(High Resolution, HR)格式vanLeer 离散对流项，用Gauss linear 格式处理拉普拉斯算子的离散，用 PIMPLE 算法解耦求解 RANS 方程，用Gauss Seidel 方法求解线性方程组.求解压力泊松方程时，GAMG(Generalized geometric-algebraic multi-grid) 和 PCG(Preconditioned conjugate gradient) 方法分别用于第1次和第2次压力修正时方程组的求解.波高的提取步骤见文献[11].

2 计算结果与讨论

2.1 受迫非共振晃荡

模型液舱长L=570 mm，宽S=310 mm，高D=300 mm[11].初始液位高度h0=150 mm.建立固结于大地的坐标系，初始时刻坐标系原点位于液舱底部中心，如图3所示.波高监测点在xOy平面上的坐标是 (0, 0.265) m.

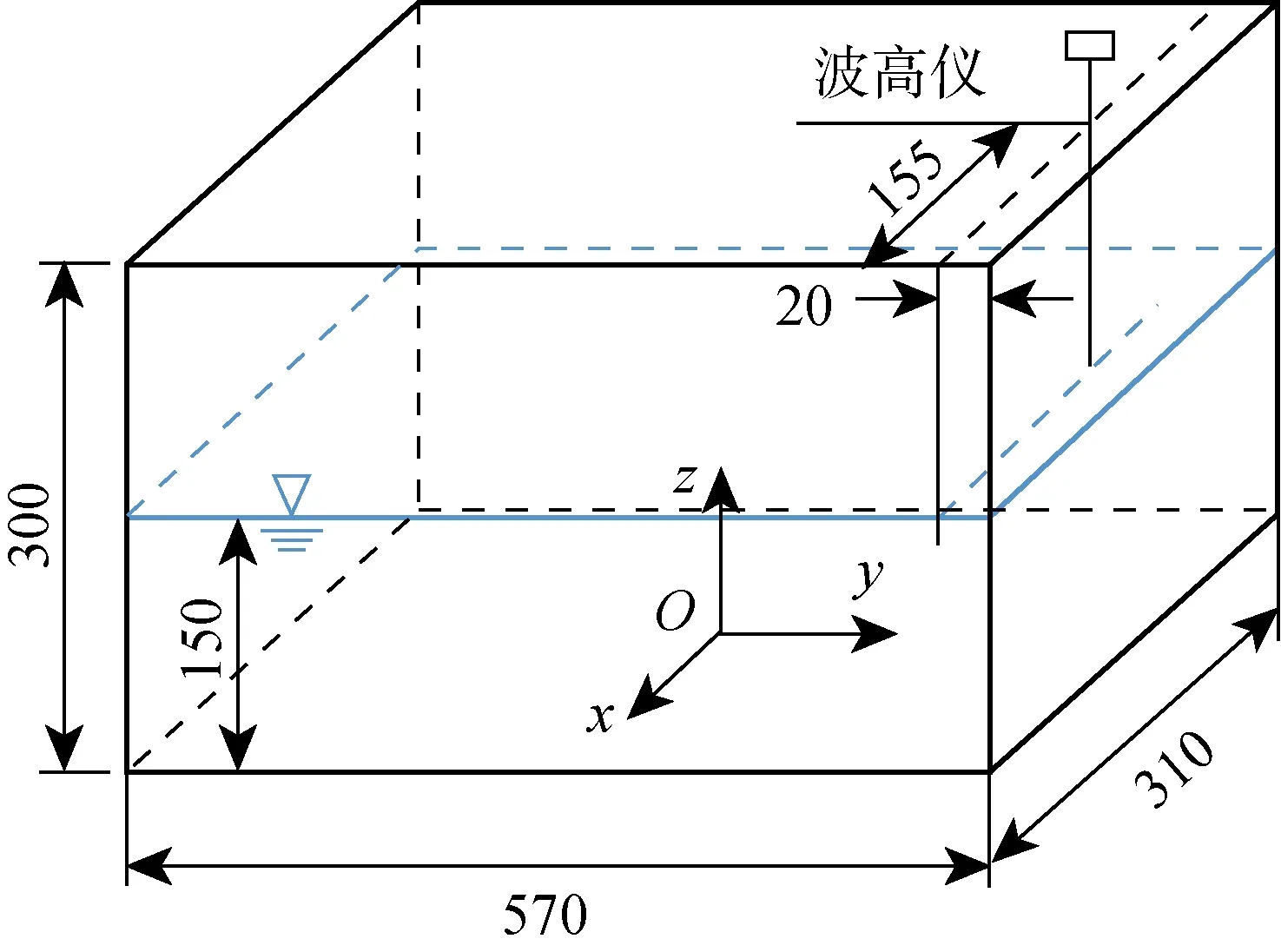
图3 非共振晃荡模型液舱和波高监测点布置(mm)Fig.3 The model tank and the wave probe of non-resonant sloshing (mm)

液舱受到简谐强迫激励：

y=-asin(ωt)

(13)

式中：a=0.005 m为激励振幅，a/L=0.008 77；ω为受迫激励频率，ω/ω1=0.583，ω1为固有频率[11].

在初始液面附近进行网格局部加密，最小网格尺寸约为 0.005 m.采用自适应步长进行计算，最大库朗数是 0.2，初始时间步长为 0.000 1 s.分别采用3种 VOF 方法(isoAdvector-c2，isoAdvector-c1和MULES方法)捕捉自由液面的位置，并将结果与试验结果[11]以及解析解[18]进行对比，如图4所示，图中η为波高.由图4可见，对于远离固有频率的非共振晃荡，波高振幅较小.3种VOF方法获得的波高时历均与解析解以及试验结果较为吻合.

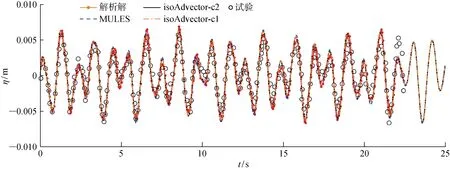
图4 监测点处波高时历对比Fig.4 The comparison of free-surface elevations at the probe

2.2 受迫共振晃荡

模型试验所用的液舱是边长L=0.6 m 的立方体，建立固结于大地的坐标系，在初始时刻，坐标系的原点在液舱底部中心[19].初始液位高度h0=0.3 m.在 w3 处设置波高监测仪，如图5所示.

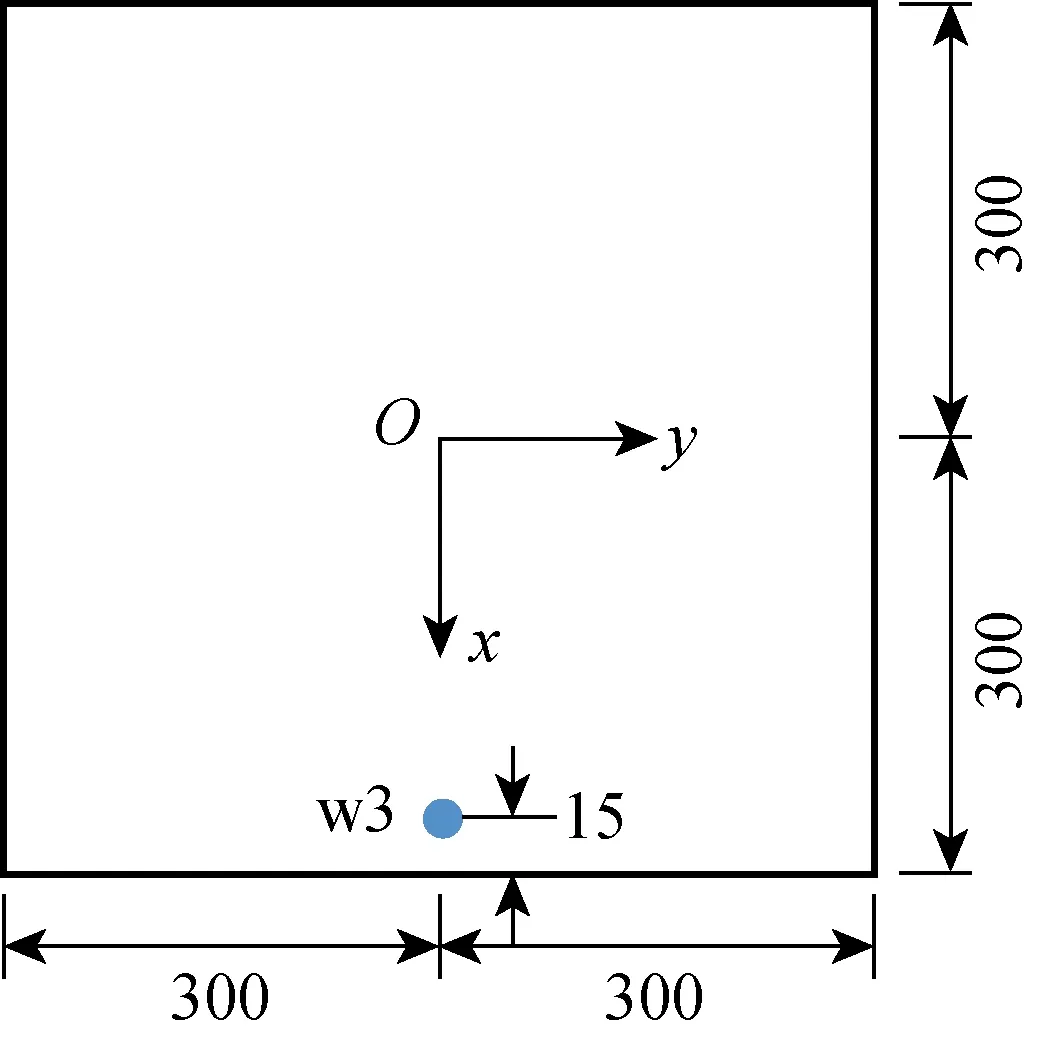
图5 共振晃荡模型液舱和波高监测仪布置俯视图(mm)Fig.5 Top view of the model tank and the wave probe of resonant sloshing (mm)

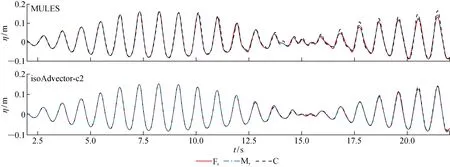
图6 波高仪 w3 处波高的网格收敛性验证 Fig.6 The verification of grid convergence for the free-surface elevations at wave probe w3

液舱受迫激励，受迫运动为简谐振荡运动：

x=asin(ωt)

(14)

式中：a/L=0.008 71；ω/ω1,0=1.037，ω1,0是一阶固有频率[11].

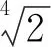
表1 不同网格的基本信息Tab.1 The information about the different meshes

为进一步进行定量比较，引入数值计算结果和试验数据间的方均根误差E：

(15)

2.2.2自由液面位置对比 分别采用3种 VOF 方法(isoAdvector-c2、isoAdvector-c1和 MULES方法)捕捉自由液面的位置，并将结果与试验结果[19]进行对比，如图7所示.由图可见：波峰的绝对值大于波谷的绝对值，表现为非线性特征；t<6 s时，各种 VOF 方法获得的波高时历和试验值吻合较好；t>6 s时，isoAdvector-c1 方法得到的波高时历和试验值相差较远，而isoAdvector-c2方法得到的波高时历和试验值较为吻合，这说明面-界面交线运动修正十分重要.3种方法得到的波高时历与试验结果的方均根误差见表2.可见，由MULES得到的Eηw3比isoAdvector-c2方法得到的Eηw3大，说明isoAdvector-c2方法的计算结果和试验值更为接近.MULES和isoAdvector-c2方法的界面厚度见表3，其中R为界面厚度与由MULES方法得到的界面厚度的比值.可以看出， isoAdvector-c2方法得到的界面厚度大约为MULES方法得到的界面厚度的1/2.

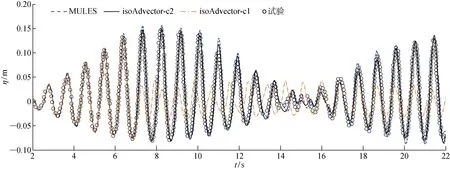
图7 w3 波高仪处波高时历Fig.7 The time histories of free-surface elevations at wave probe w3

表2 波高仪w3处波高和纵向力的方均根误差

Tab.2 The RMSE of the free-surface elevations at wave probe w3 and the longitudinal force

方法Eηw3/cmEFx/NMULES2.07033.775isoAdvector-c21.51728.902isoAdvector-c15.01368.840

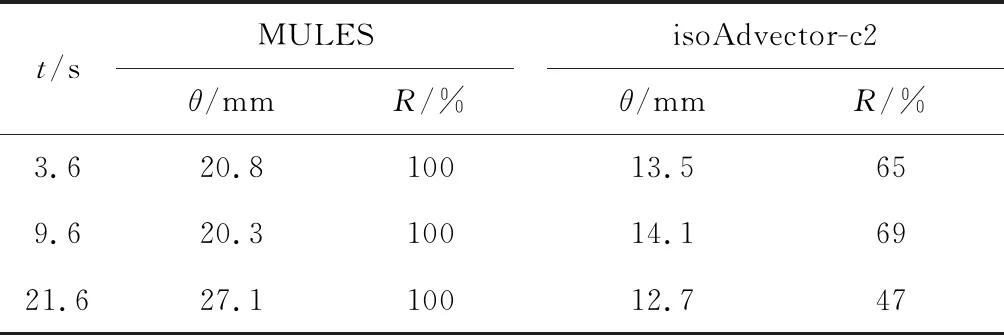
表3 界面厚度Tab.3 The interface thickness

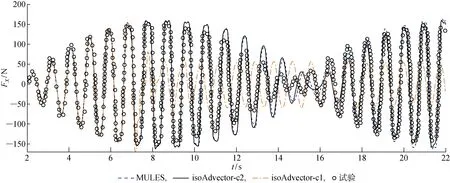
图8 晃荡纵向力Fig.8 The longitudinal force

2.2.3整体水动力载荷对比 在整个液舱各个表面对热力学压力和黏性作用力进行积分，可得到晃荡引起的整体水动力载荷.整体载荷在x方向的分量称为纵向力Fx.上述3种VOF方法计算得到的Fx如图8所示.可以看出：isoAdvector-c1 方法得到的Fx与试验值不符，原因在于采用该方法捕捉的自由液面位置和试验值偏差很大；而isoAdvector-c2 方法得到的纵向力和试验值吻合较好.同样引入方均根误差来衡量MULES和isoAdvector-c2方法计算Fx的精度.将式(15)中的波高替换为Fx即得到纵向力方均根误差EFx，结果见表2.可以看出，采用 isoAdvector-c2 方法计算得到的EFx比采用 MULES 方法计算得到的EFx更小.

2.3 单次冲击波面

单次冲击波面(SIW)[20]试验的模型液舱如图9所示，图中缩尺比为1∶20.初始液位装载率是20%，其一阶共振周期T1=2.469 3 s.沿y轴进行特别的直线激励，从而产生SIW.受迫激励位移如图10所示，中间一段强迫位移是1/2个简谐波，对应的周期T=2.469 2 s，略小于T1.1/2个简谐波激励幅值a=244 mm,a/L=0.125.

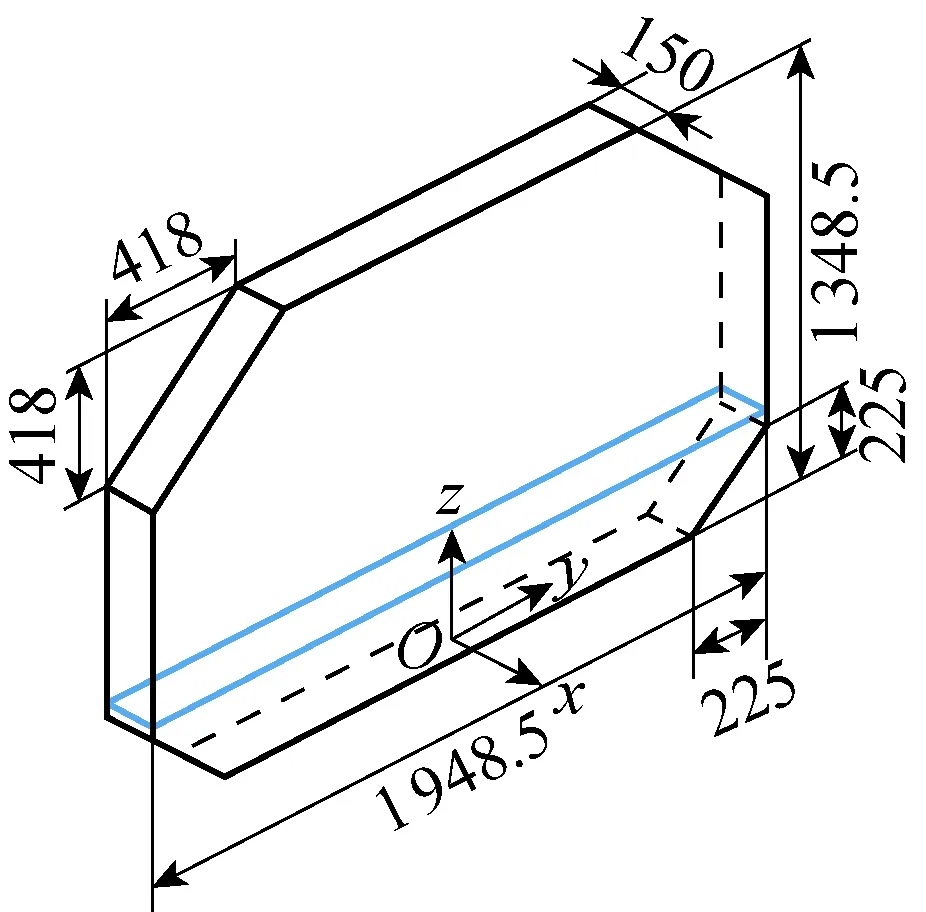
图9 SIW 模型液舱(mm)Fig.9 The SIW model tank (mm)

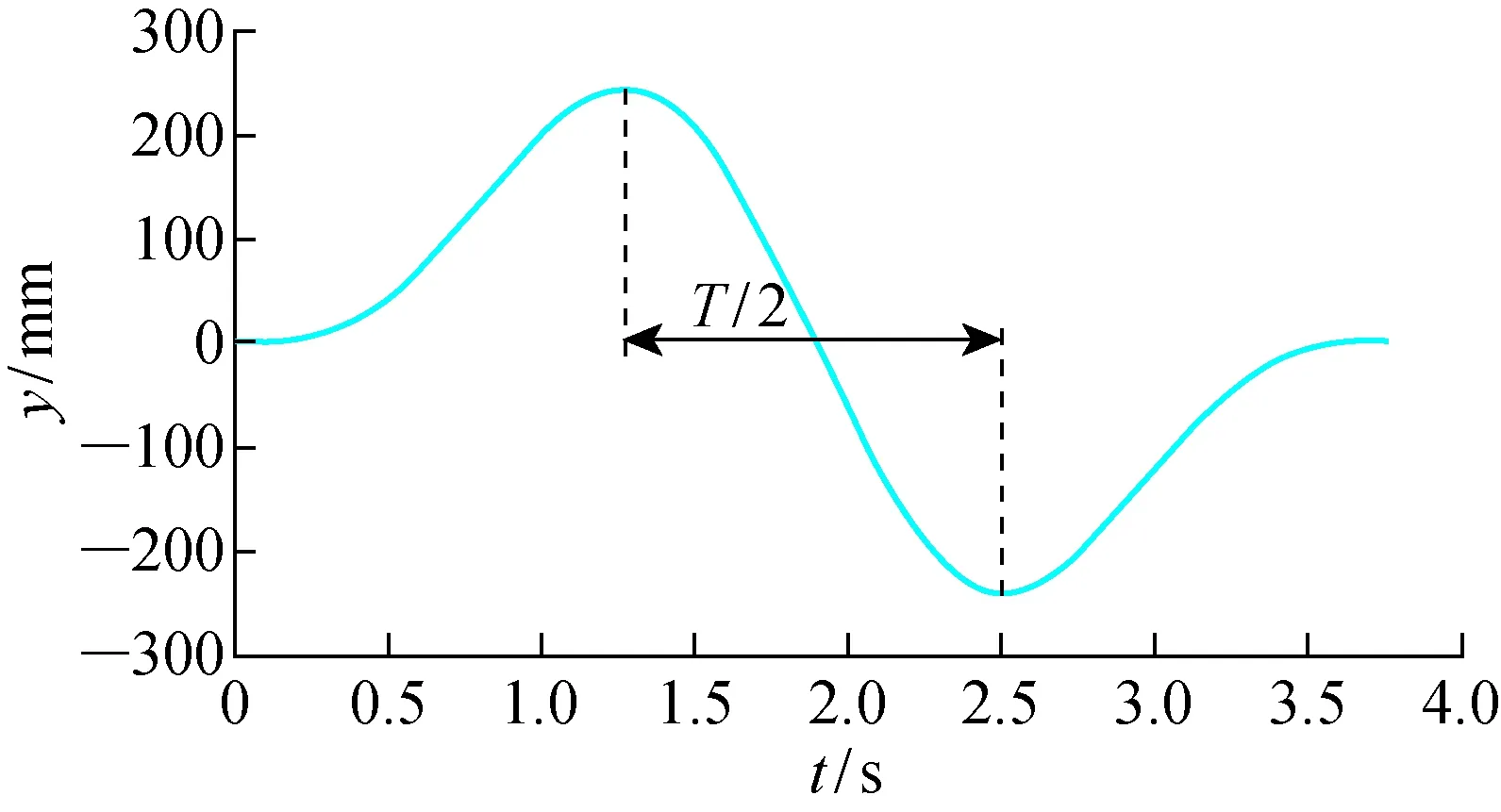
图10 SIW 外激励受迫位移时历Fig.10 The time history of the forced displacement under the SIW excitation

对初始液面附近和相界面翻卷的区域进行局部网格加密，最小网格间距为 0.005 m.采用自适应步长计算，最大库朗数为 0.2，初始时间步长设为 0.000 1 s. isoAdvector-c2和MULES 方法捕捉到的翻卷波形见图11.试验波面翻卷见文献[20]中的图16(b)，文献[20]中的图17(d)标出了波面形状，波面之外的飞溅是 Kelvin-Helmholtz 相界面不稳定性造成的[20].由图11可见，isoAdvector-c2和MULES方法捕捉得到的α1=0.5 等值线和试验的波面等值线非常相似.用isoAdvector-c2方法得到的α1=0.001 等值线和α1=0.999 等值线的间距比MULES方法得到的间距小，这和表3中的结果一致，说明isoAdvector-c2捕捉的相界面更加明锐.

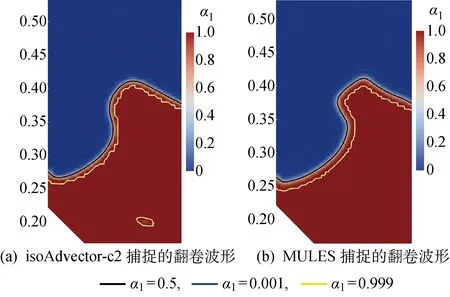
图11 SIW 冲击前波浪翻卷对比Fig.11 The comparison of the overturning waves before the impact

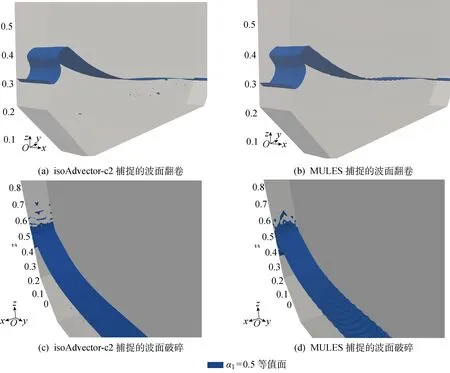
图12 SIW 冲击的三维视图(m)Fig.12 The 3D views for the SIW (m)

波面冲击壁面后引起破碎，冲击前后的三维视图对比如图12所示.由图12可见：在波峰后侧，MULES捕捉得到的波面出现了褶皱，这是代数VOF方法应用压缩格式保证界面明锐所带来的负面影响；而isoAdvector-c2方法捕捉到的波面更为平滑，波峰后侧没有出现褶皱.

3 结论

基于几何VOF方法 isoAdvector引入运动通量修正，提出面-界面交线运动修正，并采用一种近似公式，根据各个网格单元面的运动通量重构出各个单元体心的刚体运动速度，得到如下结论：

(1) 在模拟受迫非共振晃荡时，MULES、isoAdvector-c1和 isoAdvector-c2方法计算得到的波高均与试验结果和解析解吻合较好.在模拟受迫共振晃荡时，相比于 isoAdvector-c1，isoAdvector-c2方法因增加了面-界面交线运动修正，得到的波高和纵向力的结果与试验值吻合得更好.

(2) 相比代数 VOF 方法 MULES，采用 isoAdvector-c2 方法得到的波高和纵向力相对于试验值的方均根误差更小.

(3) 采用修正的 isoAdvector 方法捕捉到的两相界面的厚度大约是代数 VOF 方法 MULES所得界面厚度的1/2，两相界面更为明锐.

(4) 在模拟单次冲击波面时，isoAdvector-c2和 MULES 方法均能捕捉到和试验波面相似的波面形状，能很好地模拟波面的翻卷和破碎；基于 MULES 方法捕捉的波面在波峰后侧出现褶皱，而 isoAdvector-c2 方法捕捉到的波面没有褶皱，更加平滑.