针对气云爆炸的控制室载荷安全系数
齐心歌, 王海清, 田英帅, 陈国明
(1.中国石油大学(华东)机电工程学院,山东青岛 266580; 2.深圳燃气集团安全管理部,广东深圳 518040)
控制室是石化行业作业区内的指挥中枢,是保证工作人员安全以及生产活动正常进行的关键机构,对于维持生产设备的运转、作业的进行以及人员安全具有至关重要的作用[1]。因此对控制室的防爆进行研究,采用气体探测GDS系统(气体探测系统,gas detection system),将气体泄漏扩散造成的风险控制在控制室的爆炸载荷范围内,对于保障作业区的人员以及设备的安全具有重要意义。目前对控制室的防爆主要从两个方面进行研究:一是从设计载荷的角度,以爆炸产生的冲击波超压值来表征控制室能够承受的爆炸载荷,如国内外标准规范ASCE 41088[2]、GB50779-2012[3]等;二是从概率爆炸载荷的角度,综合考虑气体的泄漏场景、气云扩散、点火概率以及点火位置等得到作用于控制室的爆炸载荷[4-5]。以上两者可得到控制室各个方向的设计载荷以及发生爆炸事故时作用于控制室冲击波超压[6-7],但是在GDS系统的应用中,针对控制室载荷的探测阈值尚未给出明确的界定,探测载荷阈值须满足一定的安全裕度,降低探测不确定度的影响,并为应急措施的实施提供充分的预留时间。笔者基于控制室的概率爆炸载荷,充分考虑各类影响因素的不确定度,得到探测中控制室爆炸载荷的安全系数,增强GDS系统设计输入量的保守性。
1 不确定度理论
在实际爆炸载荷设计中,由于气体泄漏、扩散以及气云爆炸过程的高度复杂性,在计算过程中会涉及大量不确定性参数,是GDS系统探测有效性的关键。从不确定度着手,得到控制室的爆炸载荷,作为GDS系统设计输入量的基础。
目前被广泛认可的不确定度分类由Apostolakis首次提出,分为两类:随机不确定性和知识不确定性。随机不确定性是系统本身存在的,是固有的、不可降低的,也称为A型不确定性;知识不确定性可称为B型不确定性,是指由于知识的欠缺导致的潜在不准确性,随着知识的完备可逐渐降低[8]。因此对不确定性的分析主要围绕知识不确定性展开。
在工程应用中,对知识不确定性的分析需要从计算模型的参数入手,将输入参数的不确定性量化,并判断其对输出结果不确定性的影响。对不确定性分析应用最广泛的是经典概率方法,且有大量基于概率的不确定性方法被提出,包括蒙特卡洛法(MC法)、微分法、响应面法等,其中MC法由于原理易于实现,在多个领域得到广泛应用。
由于输入参数在不同模型对结果的影响不同,需要通过参数敏感性分析,判断其对结果不确定性的影响程度。参数敏感性分析方法包括全局敏感性分析和局部敏感性分析两类。其中局部敏感性分析方法易于实现,但每次只能分析单个参数不确定性的变化对结果的影响且对线性关系模型较为有效;全局敏感性分析方法可定量分析非线性模型的不同输入参数同时变化时产生的交互作用对输出结果不确定性的影响,本文中采用Sobol指数法对全局敏感性进行分析。
2 爆炸结果模型及参数分析
对于气体泄漏引起的爆炸事故后果需要从泄漏源、扩散过程、气云的爆炸一系列过程进行分析[9-10]。对气体泄漏源分析主要针对储罐等装置的小孔泄漏以及底部管道的断裂泄漏,因此采用伯努利方程;常用的气体扩散模型有CFD模型、高斯扩散模型、唯象模型、相似模型等,综合考虑计算效率与精确度,选择高斯扩散模型;气云爆炸的典型模型是多能法,经过了大量实验的验证以及修正,充分考虑了气体活性、局部约束、湍流加速等因素,与实际爆炸场景较为接近[11]。
2.1 气体泄漏
利用伯努利方程计算气体泄漏速率,表示为
(1)
式中,QL为气体的泄漏速率,kg/s;Cd为孔流系数,若泄漏孔为圆形,一般取1;A为孔径的面积,m2;ρ为流体密度,kg/m3;p为工作压力,kPa;p0为大气压力,kPa;u1为装置中气体流速,m/s。
根据式(1),气体泄漏过程中对泄漏速率造成主要影响的因素包括泄漏孔的直径和形状、模型采用的流量系数以及运行压力等。
2.2 气体扩散的等价气云
利用高斯模型计算过程中,气候条件(如风速、风向、湿度)、表面粗糙度等因素对计算结果产生影响[12]。
高斯模型平均浓度方程为
(2)
式中,C(x,y,z)为气体泄漏时,给定地点(x,y,z)的密度,kg·m-3;u为大气风速,m·s-1;σy,σz为侧风向和垂直风向的扩散系数,与大气稳定度以及下风向距离x有关,m;x,y,z为下风向,侧风向和垂直风向的距离,m;Hr为泄漏点源高度,m。
基于高斯扩散模型提出等价气云的概念,用均相的立方体气云来代替密度、浓度不均匀、形状不规则的非均相气云,以此来减少需要模拟的泄漏场景数量[13-14]。
计算浓度等值线,需要从x、y、z三个方向得到气体扩散距离,以x为变量表示y,将高斯模型式(2)变形,表示为

(3)
式中,σy、σz均为x的函数,取值依据Pasquill-Turner大气稳定度公式。
式(3)中,在场景范围内将泄漏源作为坐标原点,下风向为x轴,侧风向为y轴,垂直风向为z轴建立坐标系。沿x轴方向取一定步长(如1 m)并生成矩阵,在一定浓度阈值下,分别计算对应的y值。计算过程中,若x取值过大或过小,可能会出现y无实数解的情况。物理意义解释为:气体扩散过程中形成的浓度等值线可能是封闭的,并与泄漏源有一定距离,因此在一定x范围内才会有对应的y值。
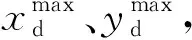
SESC=πab,
(4)
其中
式中,a、b分别为浓度等值线等价椭圆的长、短半轴;SESC为高度z一定时等价椭圆的面积。
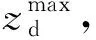
(5)
2.3 多能法计算爆炸后果
气云发生扩散后,若云团中气体浓度在爆炸极限内,遇点火源会引发爆炸事故[15]。对气云爆炸后果的分析,拟采用多能法[16],得到对建筑物破坏的影响距离。具体实现步骤如图1所示。
E=3.5×103VESC.
(6)
其中3.5×103kJ/m3为同化学计量浓度下烃-空气混合物的典型燃烧热值。
(7)
式中,R′为无量纲距离;z为爆炸中心与待分析设备的距离,m;p0为大气压力,通常取101.325 kPa。
ps=p0p′.
(8)
式中,ps为实际峰值侧向超压,kPa;p′为无量纲比拟最大侧向超压。
由于爆炸事故对设备以及建筑等造成损害的主要形式为冲击波超压,因此以冲击波超压值作为输出参数。
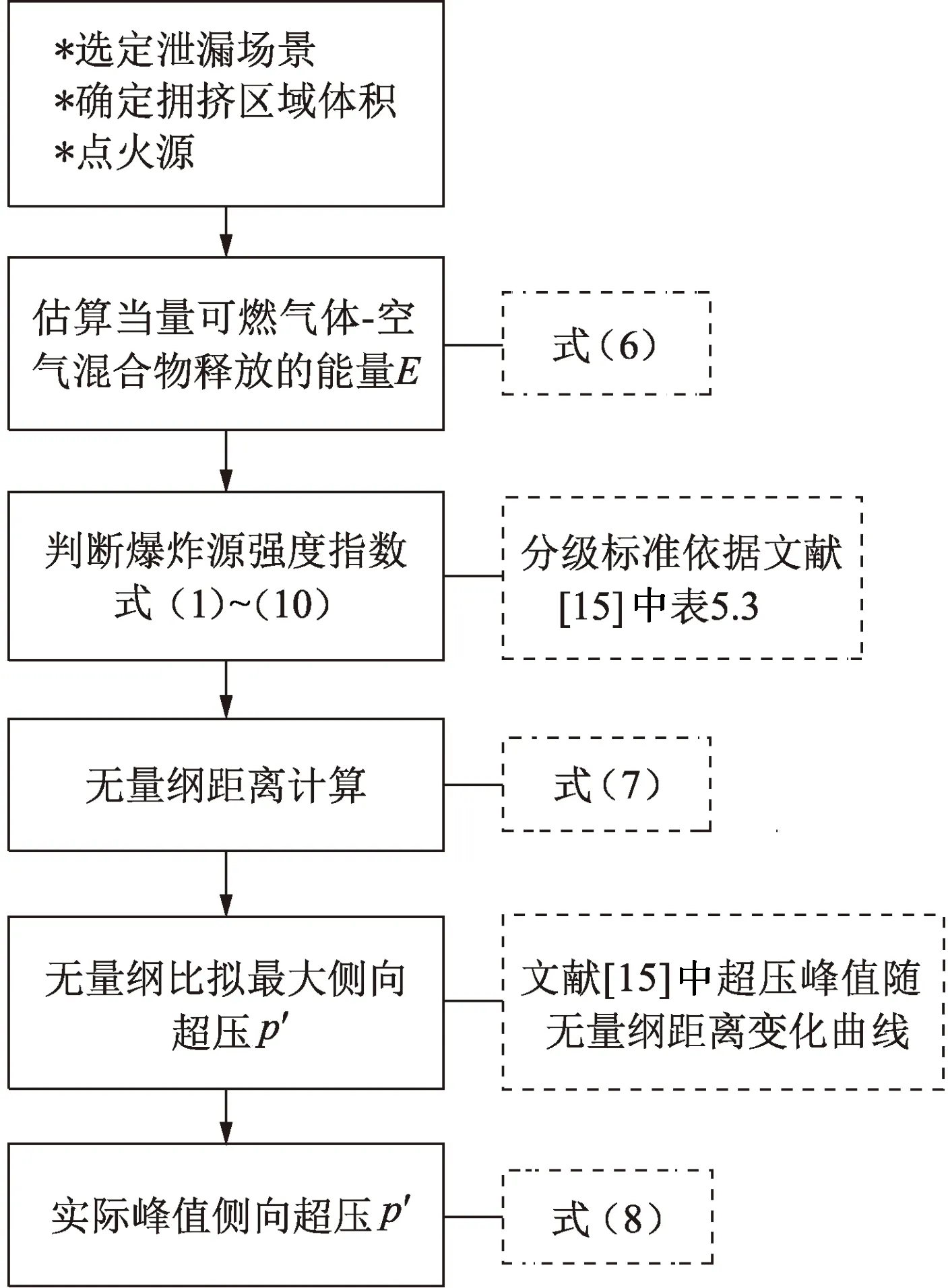
图1 多能法计算爆炸后果流程Fig.1 Flow chart of explosion consequence calculation by multi-energy method
3 基于MC模型的参数不确定度
基于MC模型计算不确定度步骤如下:
(1)确定不确定度来源。不确定度分析的主要目的是依据模型的不确定性与输入的不确定性修正预测结果。对计算模型中涉及的参数进行分析,确定不确定性参数。
(2)确定不确定性参数的概率特征并生成随机输入样本。依据以往的扩散场景、历史数据等拟合得到输入参数的概率密度函数,基于概率密度函数用抽样法得到离散分布的样本[17-18]。样本的大小以及抽样方法的选择决定了MC模型模拟的精度。
样本数量可通过统计容许极限(a%,b%)确定。统计容许极限是指在b%的置信区间下,保证抽取的样本在其分布中的比例不小于a%。样本数量M可确定为
(9)
目前常用的样本抽样方法有分层抽样法、简单随机抽样法、拉丁超立方抽样法(Latin hypercube sampling,LHS)以及汉莫斯里序列抽样法等。其中汉莫斯里序列抽样法与LHS样本分布较均匀,且LHS可以在较少样本的情况下达到更高的精度,因此选择LHS[19-20]。假设需要在m维空间抽取n个样本:①在参数取值范围内,将每一维度分成n个互不重叠区间(通常使用均匀分布,使得区间长度相同);②在每一维度的每一个区间中随机抽取一个点;③从每一维度随机抽取步骤(2)中的点,组成矩阵,作为输入样本。
(3)以生成的样本为输入计算对应的输出,并利用期望与标准差的值对不确定性分析结果进行表征,得到输出结果的不确定度,表示为
(10)
(11)
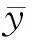
4 安全系数
4.1 不确定性参数的全局参数敏感性
在敏感性分析中,散点图可定性获得输入参数的不确定性对结果的影响。散点图是将输入量作为横坐标,输出量作为纵坐标,利用抽样法获取大量样本并得到对应输出结果,在坐标系中描绘,可定性观察输入量对输出量的影响。虽然具有形象直观的特点,但不能定量得到两者的关系,因此在散点图的基础上,需采用其他全局敏感性分析法对输入参数与输出结果之间的关系进行定量分析。
目前,最常用的全局敏感度分析方法为Sobol指数法[21-22],基本思想是利用总方差表示全部变量对输出结果的影响,利用偏方差表示单变量或多变量对输出结果的影响,不同输入参数对输出结果的影响程度依据该参数在总方差中所占的比例来衡量。分析步骤如下:
(1)假定某一函数Y,可表示为自变量为X的一系列函数之和,即
(12)
其中
(13)
(2)参数xi的方差可表示为
(14)
总方差计算为
(15)
(3)输入参数xi对输出y的影响可通过一阶敏感性指数确定,表示为
(16)
4.2 安全系数计算
得到输入参数的不确定性产生的综合不确定性影响为
(17)
式中,p为不确定参数数量。
进而得到安全系数为
sc=1-uc.
(18)
综上,对控制室爆炸载荷安全系数进行分析,需综合考虑气体泄漏、扩散以及形成气云的爆炸过程。通过分析不确定度来源得到不确定性参数,通过全局敏感性分析得到不同参数对输出结果的影响程度,整体分析步骤如图2所示。
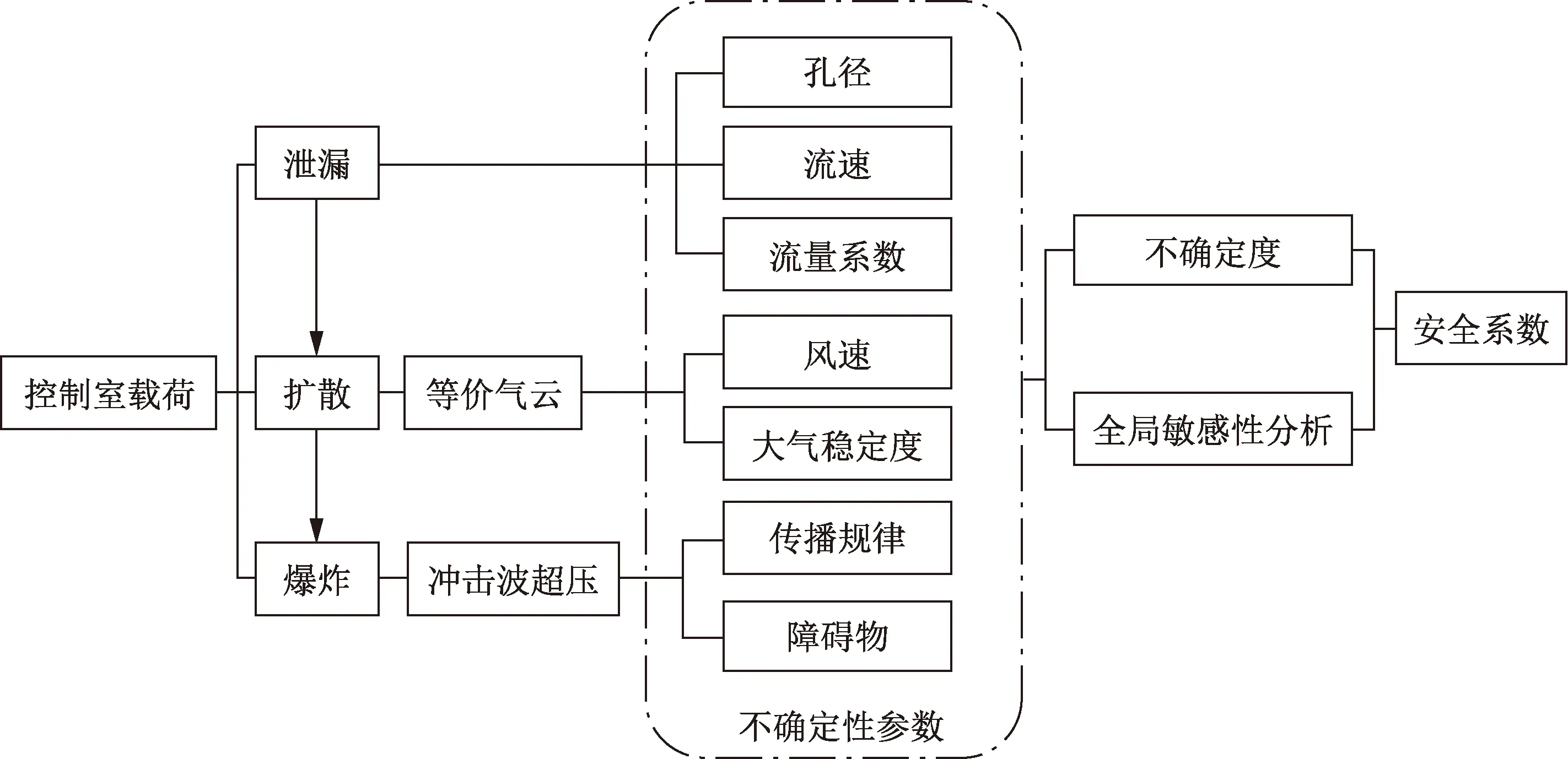
图2 控制室载荷安全系数计算流程Fig.2 Calculation flow of safety coefficient
5 案例分析
以某LNG罐区为例,假设罐区为矩形,平面尺寸为260 m×240 m;有两座并排LNG液态储罐,尺寸为:底面直径80 m,高度22 m;储罐中心与控制室的水平距离为50 m,当地气象条件为全年风速分布在1~5 m/s。以其中某一储罐底部管线破裂为例,分析气体泄漏扩散导致的爆炸事故形成的冲击波超压过程,进而分析其对控制室设计的影响并得到其安全系数。
5.1 输入样本选择
利用蒙特卡洛方法对不确定度进行分析,需要利用拉丁超立方抽样法确定输入样本。
(1)输入样本大小确定。依据式(9),选取置信区间为97%,即a=b=97,解不等式得到N>116。样本值可取为大于116的任意实数值,但样本过大,导致计算效率降低,因此案例中取样本容量为120。
(2)不确定性参数取值区间确定。选取不确定性参数为泄漏孔径、介质流速、流量系数、环境风速,概率密度函数均为均匀分布。根据实际工况,选取不确定性参数的取值区间如下:泄漏孔径的取值区间拟选择中孔泄漏,孔径范围为0.01~0.05 m;介质流速区间依据介质在储罐与管线以及其他设备中的不同流速来确定,取0~4 m/s;流量系数的取值与泄漏孔形状有关,当形状为圆型、三角形、矩形或其他形状时,流量系数取为0.9~1.0;环境风速取值区间的确定依据当地的气象情况统计数据,为1~5 m/s。在此区间内生成输入参数的样本矩阵。
5.2 不确定度与参数敏感性
气体泄漏孔径泄漏后发生扩散,基于等价气云理论,将样本矩阵带入式(1)~(5)得到扩散形成的等价气云体积,其中式(2)~(3)中浓度阈值的确定依据LNG的气体爆炸下限;选择多能法最为气体爆炸事故后果分析的方法,依据式(6)~(8)得到气云爆炸导致的冲击波超压。利用蒙特卡洛方法,依据式(10)~(11)计算得到输出值的均值与标准差,标准差即为不确定度。
爆炸超压与输入参数的散点图(图3)可直观地展示输入参数的不确定性对输出结果的影响,各个输入参数的归一化拟合斜率比值近似为泄漏孔径:流速:流量系数:风速=28.0∶1.0∶4.8∶21.6,可以看出输入参数对结果影响依次为泄漏孔径>风速>流量系数>流速,其中泄漏孔径与风速对结果影响较大且呈现不明显的线性关系,其次为介质流速,流量系数的变化对输出量的影响很小。为对非线性关系进行量化,此处利用Sobol指数法对等价气云爆炸模型作参数敏感性分析。式(12)~(16)描述了Sobol指数法,依据式(12)~(14),建立N×2D(其中N为样本数,D为输入变量数目)的样本矩阵,样本的建立同样利用拉丁超立方抽样法。将矩阵的前D列设置为矩阵E,后D列设置为矩阵F,构造N×D的矩阵EFi(i=1,2,…,D),即用矩阵E中的第i列替换矩阵A的第i列,因此得到输入矩阵E,F,EF1,EF2,EF3,EF4,由此就有(D+2)×N(即720)组输入数据,因此将有720组超压输出值,如图4所示。依据式(15)~(16)可得到参数的敏感性分析结果,如表1所示。
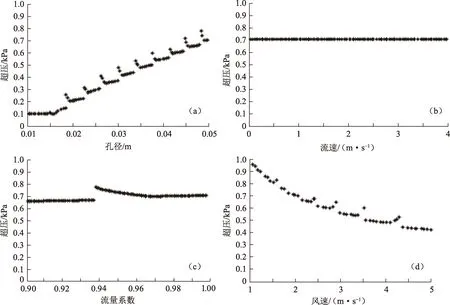
图3 样本区间内超压值散点图Fig.3 Overpressure scatter plot in sample interval
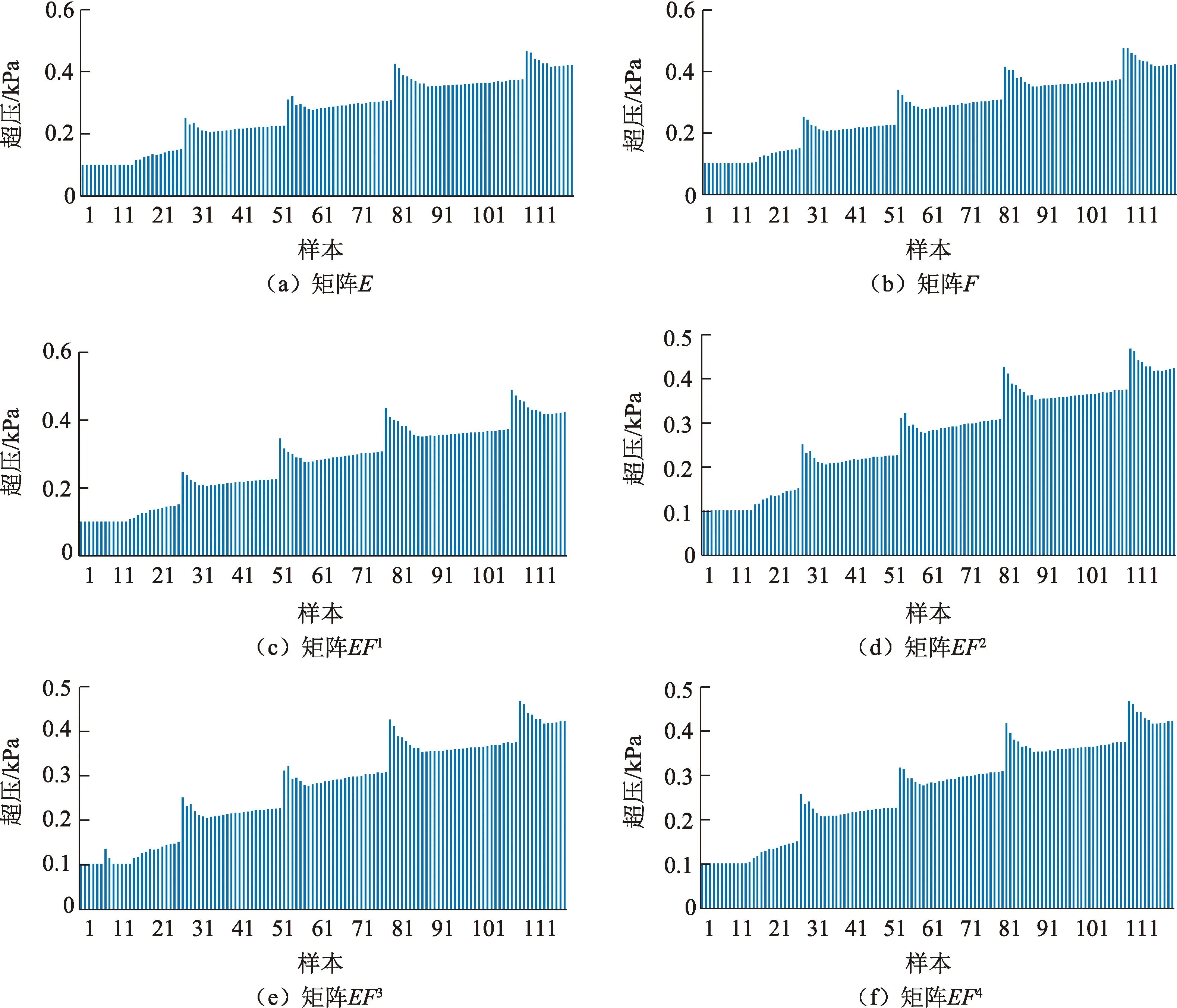
图4 参数敏感度过程矩阵超压柱形图Fig.4 Overpressure histogram of process matrix to calculate parameter sensitivity

表1 不确定度与敏感性分析结果
在此场景下,依据式(17)得到安全系数为sc1=1-19.8%=80.2%,从敏感性指数可以看出,泄漏孔径与环境风速的变化对输出结果影响较大。
作为对比,假设储罐中心与控制室的水平距离改变为80 m,其他参数不变,得到该场景下的不确定性与参数敏感性分析结果,如表2所示。
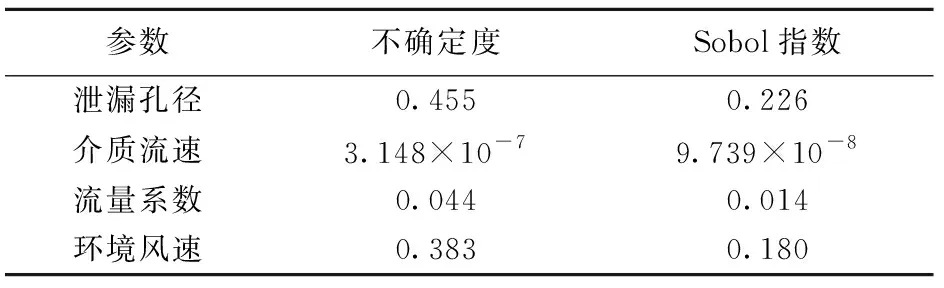
表2 不确定度与敏感性分析结果(距离改变)Table 2 Results of uncertainty and sensitivity (distance changing)
该场景下的安全系数为sc2=82.8%,与参数改变前得到的安全系数基本一致,不确定度与参数敏感性的分布变化不大。
为验证安全系数的准确度,假设设备工作压力发生改变,得到输入参数的不确定度与Sobol指数,如表3所示。该场景下的安全系数为sc3=82.86%。
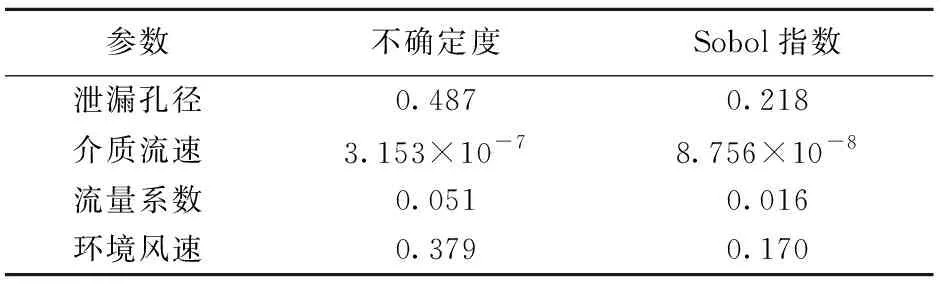
表3 不确定度与敏感性分析结果(工作压力改变)Table 3 Results of uncertainty and sensitivity (working pressure changing)
由此可见,安全系数随场景的不同而发生一定改变,但数值一般约为80%,因此对建筑物能够承受的冲击波超压阈值进行分析时,需考虑输入参数与模型不确定度的影响,并依据泄漏场景确定对应的安全系数。且安全系数的应用对于增加计算结果的保守性以及事故防控具有重要意义。
6 结 论
(1)以等价气云爆炸事故为基础,综合考虑了气体泄漏扩散过程与气云爆炸过程中的不确定性因素,实现了以控制室为代表的建筑物爆炸载荷安全系数的确定。
(2)应用于某LNG罐区,得到不同场景下的安全系数,增加了控制室等建筑物冲击波超压爆炸载荷的保守性,为GDS系统探测设计输入提供理论支持。

