垂直井筒内悬挂管柱屈曲演变有限元分析

张 强, 蒋 豹, 崔 巍,刘 巨保, 朱 昱

(东北石油大学机械科学与工程学院,黑龙江大庆 163318)

随着深井、超深井等钻井技术不断深入,受井筒约束的管柱,井底受压段极易发生屈曲,管柱屈曲后与井壁进行碰撞、摩擦,极易造成管柱的快速失效。Lubinski等[1]研究了钻柱在垂直井眼中的稳定性,给出了钻柱正弦屈曲的临界载荷。Lubinski等[2]利用能量法推导了等螺距和轴向压力的关系式。Kwon等[3]采用非等螺距假设,分析了自重作用下垂直管柱的螺旋屈曲。Hajianmaleki等[4]采用显式有限元法,研究了垂直井有重管柱的屈曲问题。Mitchell[5]、Lukasiewicz[6]、Thompson[7-8]和Gulyayev等[9]采用微分法、能量法、实验法和有限元等方法研究了管柱的屈曲问题。国内学者也对管柱屈曲进行了研究,高国华等[10]给出了管柱正弦和螺旋屈曲方程的渐进解。张永弘等[11]用三维光弹性应力冻结法实验研究了管柱螺旋屈曲问题。姜丽红等[12]用DQ单元法分析了端部约束对钻柱正弦屈曲的影响。黄文君等[13]用最小势能原理研究了边界条件对无重管柱螺旋屈曲的影响。孙友宏等[14]利用打靶法进行了管柱的屈曲分析。岳欠杯等[15]用能量法与实验法研究了井筒内受压杆管后屈曲。尹飞等[16]研究了外压作用下套管侧向屈曲。Liu等[17]采用打靶法研究了有重管柱的后屈曲问题,张强等[18]采用慢动力法研究受压扭管柱的静力屈曲问题,但均未考虑井筒的约束作用。王尊策等[19]基于梁-梁接触理论对分层采油管柱进行了屈曲分析。张强等[20]采用慢动力法研究了悬挂管柱刚好发生螺旋屈曲的问题。李子丰等[21]回顾了油气井杆管柱力学研究进展,Gao等[22]展望了悬挂管柱屈曲问题的研究方法,提出连续接触段采用微分方程的设想。黄文君等[23]根据这个设想将管柱屈曲问题转化为非线性方程组。笔者摒弃常规方法中管柱屈曲挠曲线的假设,施加初始扰动力,虚拟较大的阻尼比,提出正向和逆向加载法,研究不同长度管柱的屈曲过程。

1 模型建立

1.1 力学模型

正常作业的钻柱,下入过程中的套管柱,起下过程中的油管柱等,管柱模型为上端悬挂,下端自由[24]。如果钻压过大或井下受阻,在管柱自重、摩擦力等载荷作用下,管柱下端受压,易引起管柱自身屈曲。为此建立了如图1所示的力学模型,管柱位移边界取上下两端铰支,上端施加悬挂拉力FT,下端约束轴向位移,下端的约束反力即为井底受压载荷FC。

(1)

式中,L为管柱总长度,m;E为管柱的弹性模量,Pa;I为管柱横截面对中性轴的惯性矩,m4;q为管柱的单位长度重力,N/m。

同理,可得井底压力FC和井口悬挂拉力FT,表示为

(2)

(3)

式中,FC为井底压力,N;FT为井口悬挂拉力,N;LC为管柱受压段长度,m;LT为管柱受拉段长度,m;ξC为受压段无因次长度;ξT为受拉段无因次长度。

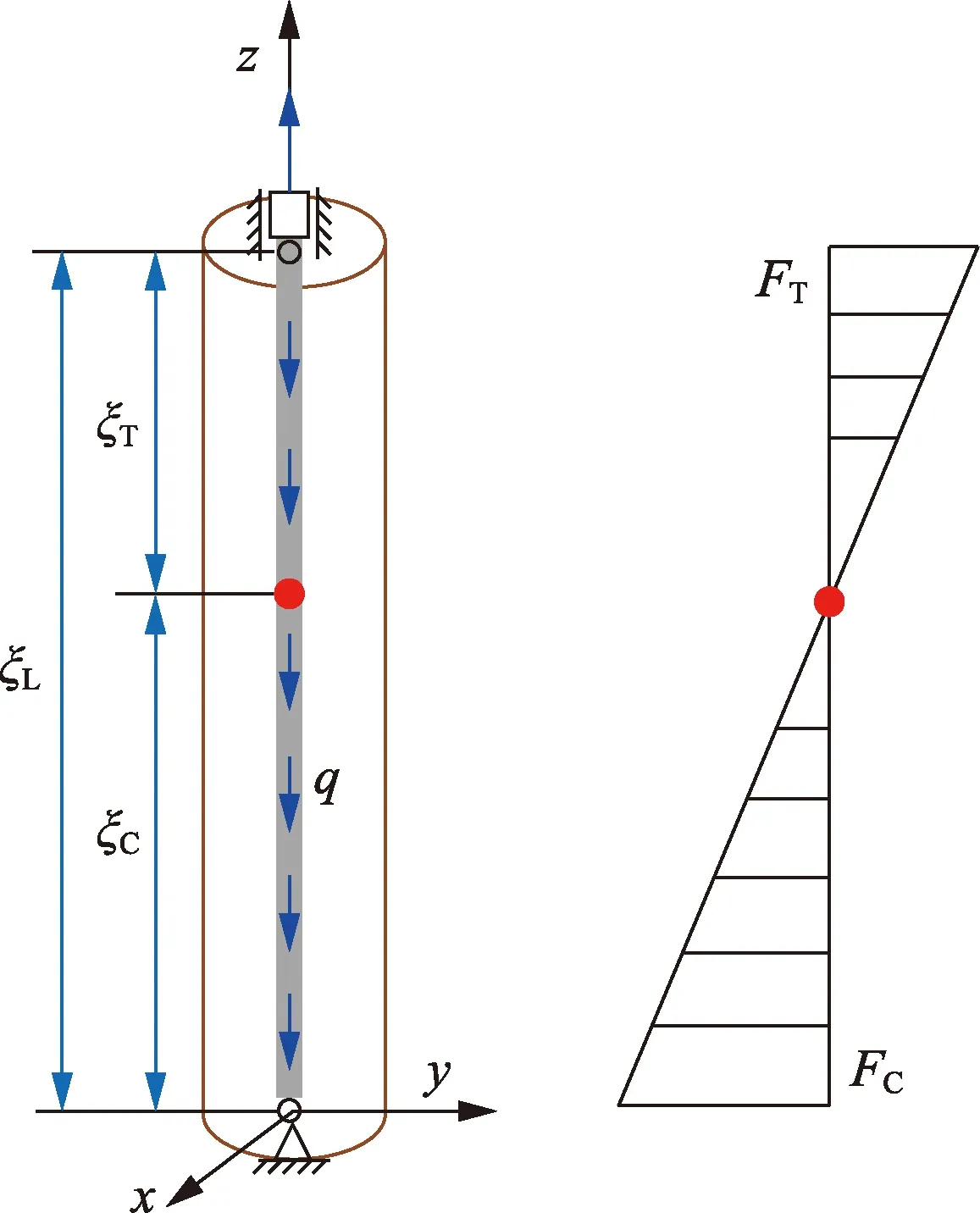
图1 管柱屈曲力学模型Fig.1 Mechanical model for buckling of suspended tubing

1.2 基本假设

力学模型做如下假设:

(1)管柱在井筒内的初始状态是完全竖直的。管柱与井筒之间有初始环空间隙存在,管柱变形前轴线与井筒轴线完全重合。

(2)管柱屈曲后与井筒内壁面接触,考虑管柱与井筒之间摩擦力的影响。

(3)研究管柱屈曲的最终稳定状态,忽略管柱上提或下放过程中的瞬态影响。

(4)忽略接头等部件对屈曲的影响。

因此在不同的管柱总长度条件下,利用新建立的力学模型,通过减小井口的悬挂拉力,将使管柱下端的压力增大,使管柱发生屈曲。

2 计算方法

2.1 慢动力法

慢动力法是利用动力学方法按照一定方式施加恒定外载荷,引入惯性力和阻尼力,考虑时间积分效应,设置较大的虚拟阻尼,计算一定的时间,求解动力响应直至稳定。也就是利用动力学方法解决静力屈曲问题[19]。

考虑悬挂管柱与井筒的非线性接触,为了解决井筒内管柱屈曲过程的收敛困难和算法不稳定性问题,利用无接触管柱静力屈曲的慢动力法[18,20]进行管柱非线性接触的慢动力分析。

2.2 动力学方程

采用有限元法依据间隙元理论[25],经过梁单元和间隙元的拼装,管柱屈曲的动力学方程为

(4)

其中

F(t)=Fw(t)+Fn(d)(t)+Fτ(d)(t),

C=αM.

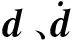
取第1阶的固有频率f作为模态阻尼比,可得阻尼比ζ与质量阻尼的关系式为

α=4πfζ.

(5)

不考虑预应力的影响,两端铰支条件下管柱第1阶的固有频率为

(6)

式中，f为管柱频率，Hz;ρ为管柱密度，kg/m3;A为管柱横截面积,m2。

输入较大的阻尼比ζ,采用Newmark直接积分法对式(4)进行隐式有限元求解。若已知t时刻管柱的位移、速度和加速度,则可计算出t+Δt时刻管柱的动力响应。随着计算时间延长管柱屈曲构型趋于稳定,各节点无速度和加速度,方程(5)可退化成静力屈曲问题,实现用慢动力法对管柱静力屈曲的求解。

2.3 载荷施加

外载荷包括井口悬挂拉力FT和管柱自重载荷qL,施加方式采用2种方法:正向加载法和逆向加载法。

(1)正向加载法。在一定时间内,按照正弦函数的方式,将外载荷施加到最大值,并一直保持。通过调整ξC值,进行反复试算,观察管柱挠度的计算结果是否屈曲。图2给出了外载荷和扰动力曲线。

管柱上端悬挂拉力FT(t)和管柱重力Fg(t)的施加函数分别为

(7)

(8)

其中

T=1/f,

mg=qL.

式中,m为管柱总质量kg;g为自由落体加速度,m/s2;T为管柱固有周期,s。

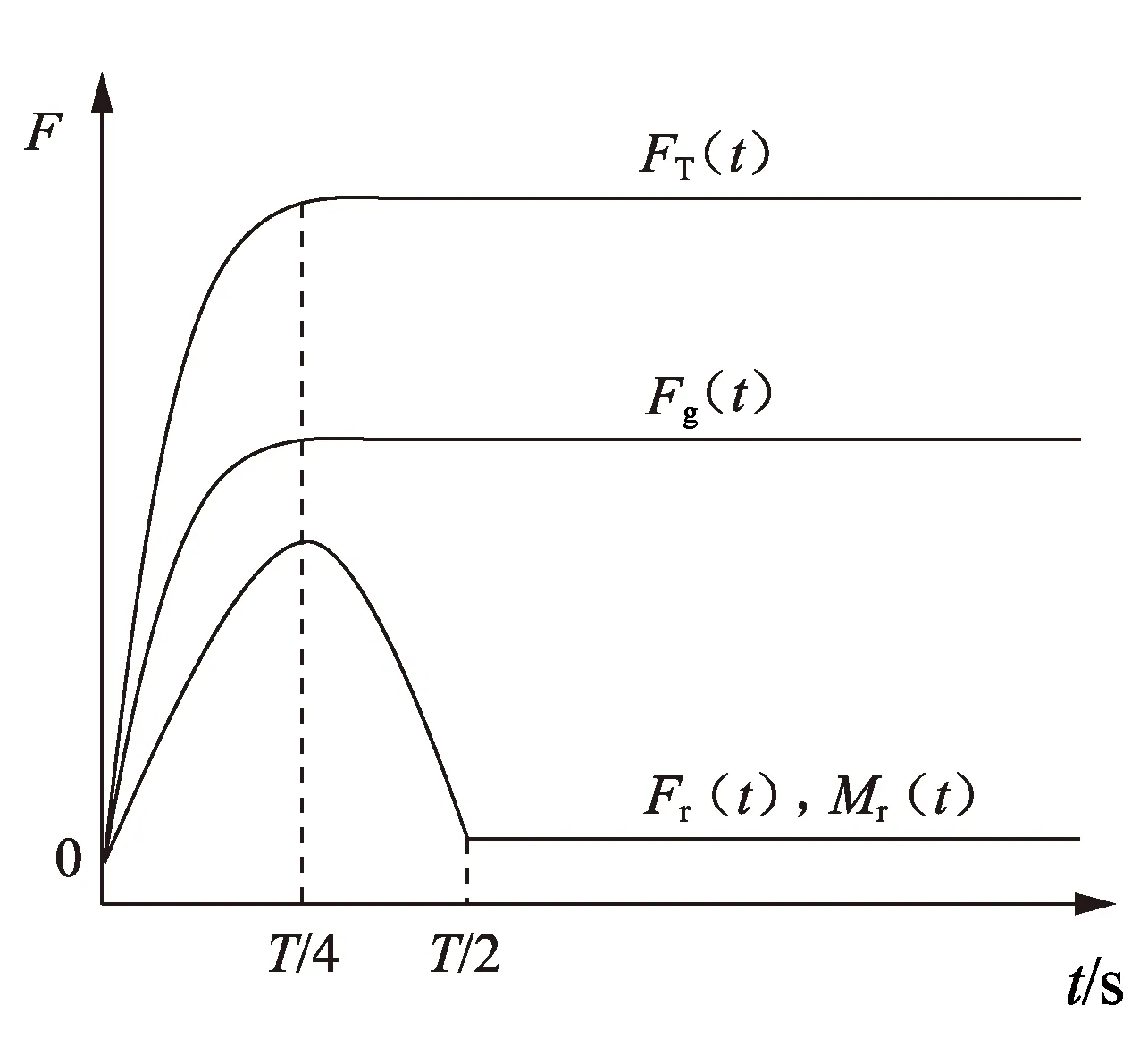
图2 正向加载法中的载荷施加Fig.2 Load applied in forward loading method

正向加载的最终悬挂拉力FT,end为

(9)

为了易于屈曲,施加了初始扰动,在管柱下端施加扰动扭矩Mr(t),在管柱受压段中部施加横向扰动力Fr(t),施加函数分别为

(10)

(11)

扰动扭矩Mr0和横向扰动力Fr0取单位载荷,计算总时间取2个周期,即tend=2T。外载荷按照正弦波施加能够减小对管柱的冲击,使管柱响应更平稳。微小扰动力是在初始施加,在后续分析中撤销,不会影响管柱屈曲的临界载荷。本文中采用初始扰动力方式,既保持了管柱结构的完整性,又实现了初始缺陷的施加。采用此种加载方式通过调整ξC反复计算,便会计算出管柱稳定的正弦和螺旋屈曲构型。

(2)逆向加载法。首先按照正向加载法获得超过一个多螺距的屈曲构型,然后上提管柱,逐渐增大悬挂拉力,从而减小管柱下端压力,使管柱依次经历螺旋屈曲和正弦屈曲构型,计算对应的临界载荷。图3给出了逆向加载法的悬挂拉力曲线。

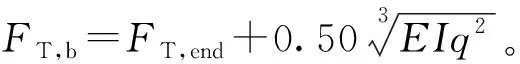
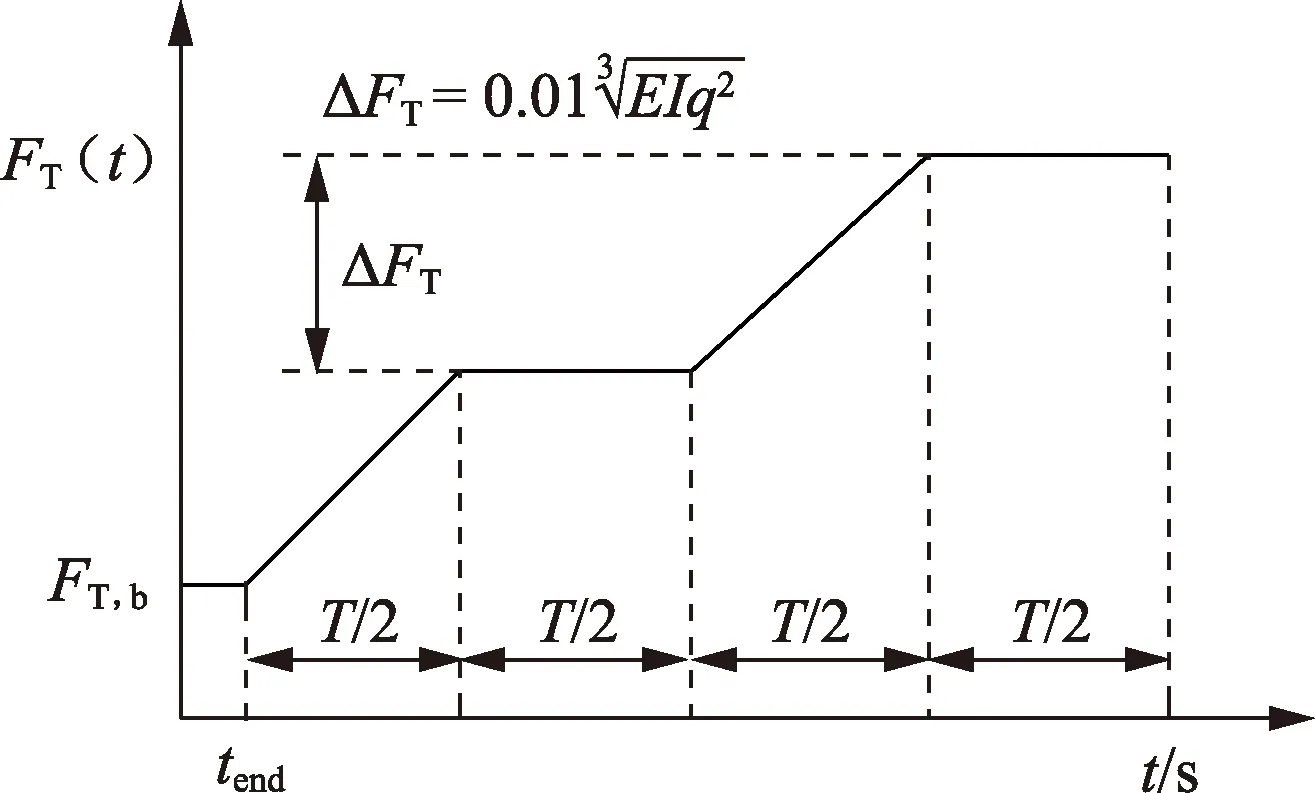
图3 逆向加载法中的载荷施加Fig.3 Load applied in backward loading method

3 计算结果分析

3.1 计算参数

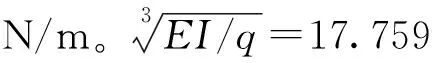
3.2 正向加载法螺旋屈曲分析

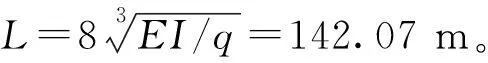
提取管柱受压段每1/4段长度位置的横向挠度v和u,位置从上到下依次记为1、2和3。图4给出了这3个位置处挠度(u/rC和v/rC)随时间变化曲线,图5给出了各个计算时间点的螺旋屈曲稳定过程的平面二维图,图6给出了各个计算时间点管柱的三维空间屈曲构型。

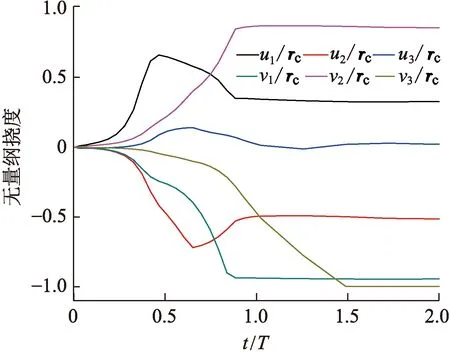
图4 挠度随时间变化曲线Fig.4 Deflection curve with time

由图4可见,计算时间达到2个周期时,各点的挠度保持常值,管柱不存在速度和加速度,解决了采用慢动力方法计算管柱静力螺旋屈曲问题。

由图5可见,当t<0.37T时,管柱与井壁未产生接触;当t=0.37T时,管柱与井壁刚好有一个接触点;当t=0.47T时,管柱与井壁正好产生两处接触,管柱挠度具有螺旋屈曲特征;当t=0.65T时,管柱与井壁产生三处接触;然后随着时间增加,中间的接触点逐渐往两侧扩展,形成连续段接触;当t=1.72T时,连续接触段形成了一个完整螺距,且不再随时间变化。

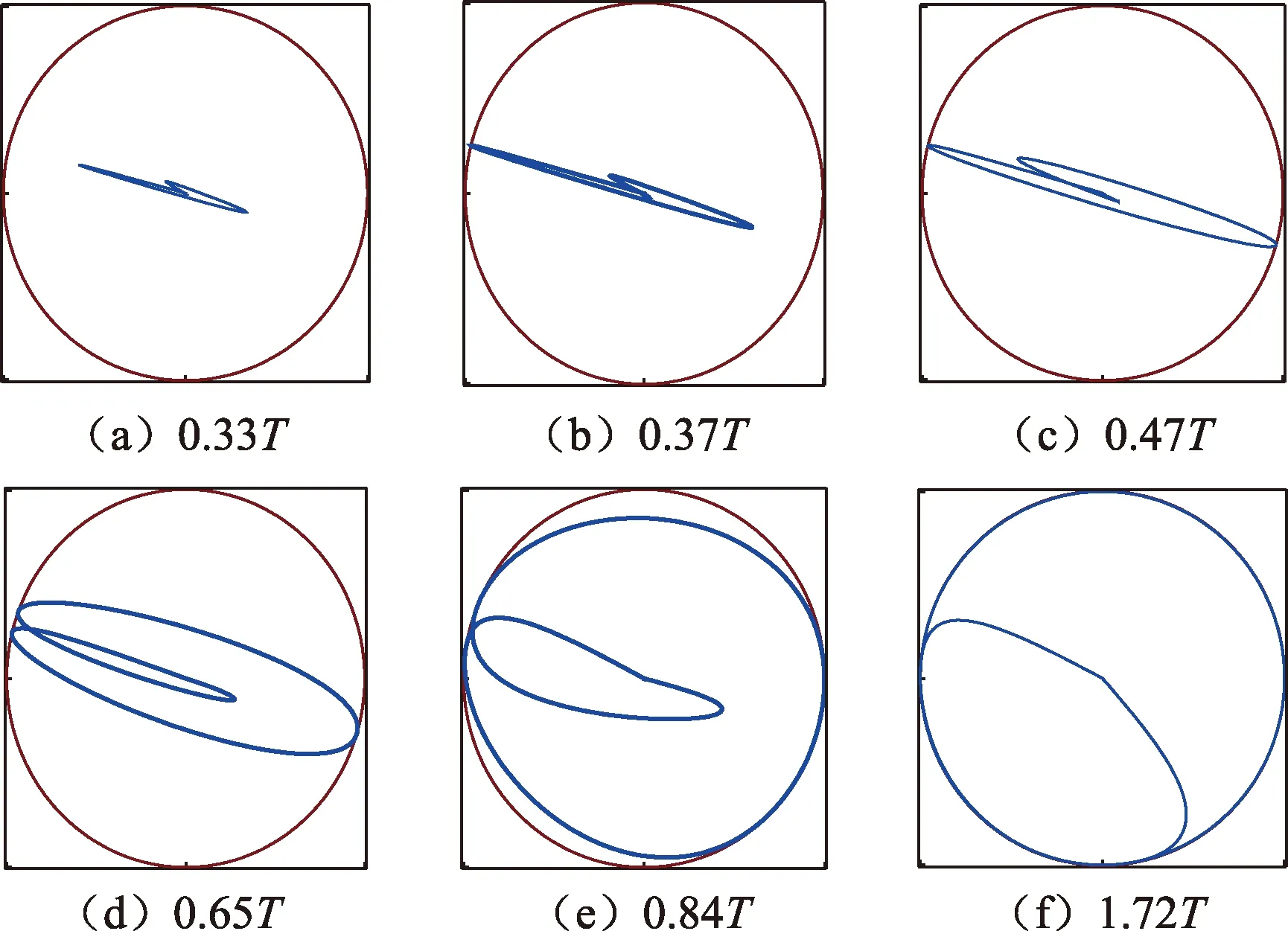
图5 正向加载法中螺旋屈曲的稳定过程Fig.5 Stable process of helical buckling in forward loading method

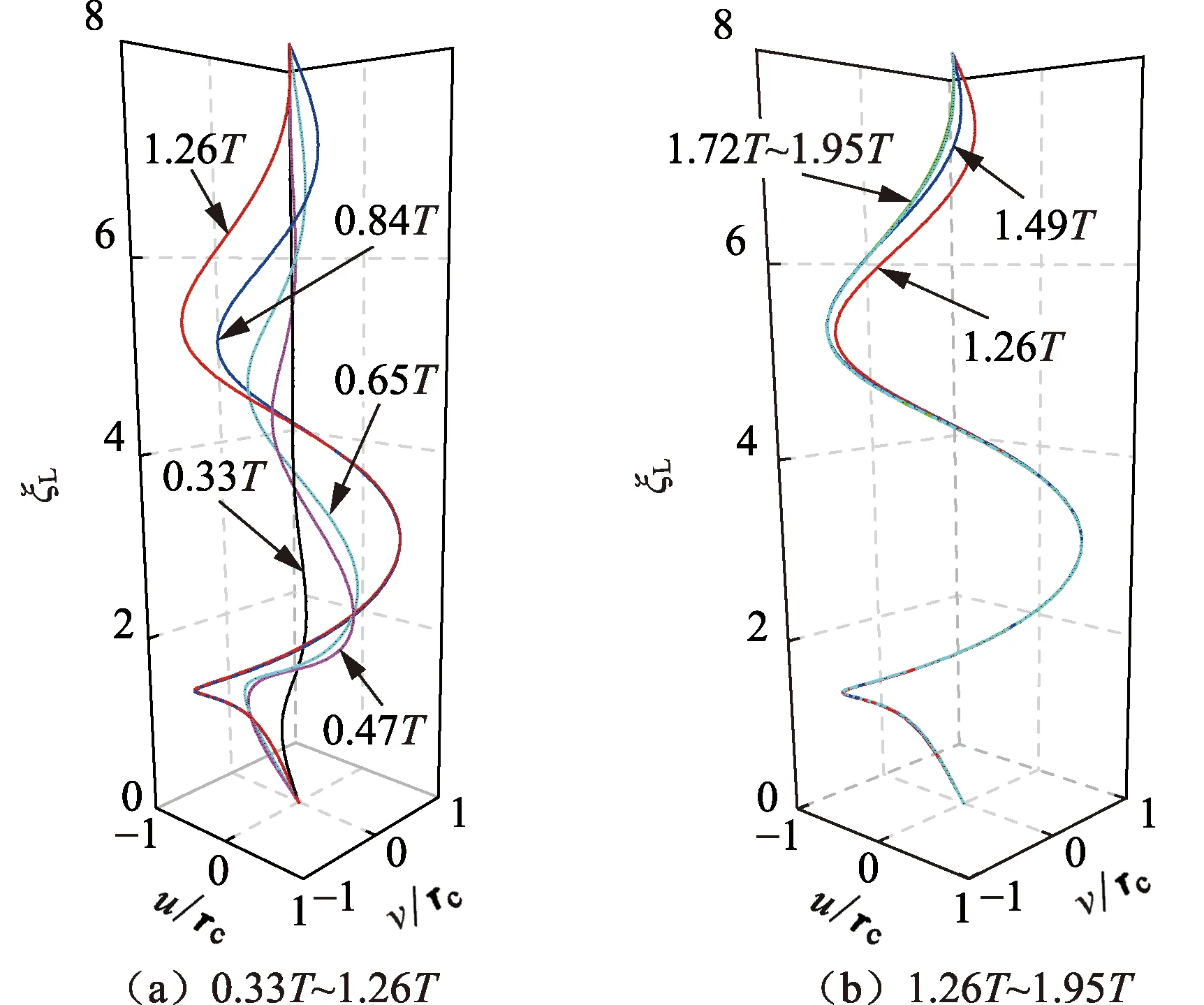
图6 三维空间屈曲构型Fig.6 Buckling configuration in 3D space

从图6可见,当t≤1.26T时,屈曲构型随着时间增加变化较大;当1.26T1.72T时,管柱的三维空间屈曲构型不再随时间增加而产生变化,说明已经达到稳定状态。

综上所述,采用正向加载法,计算时间在2个周期内能够得到稳定的螺旋屈曲构型。

3.3 逆向加载法屈曲过程分析

取无因次长度ξL=8,采用逆向加载法,图7给出了螺旋角随管柱下端受压载荷变化曲线,螺旋角以第1接触点之间的角度度量,第1接触点的说明如图8所示。

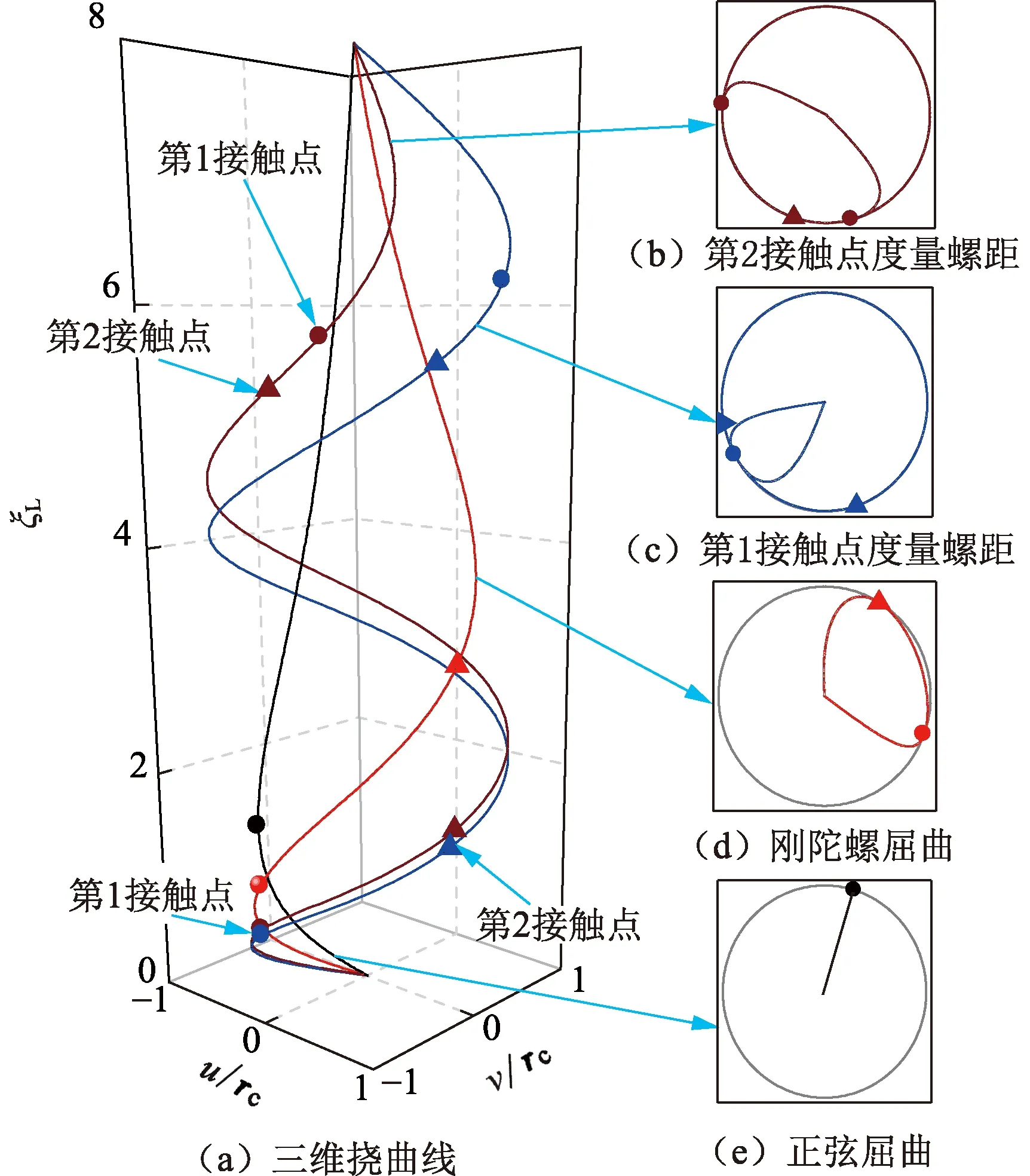
图8 各种临界载荷对应的屈曲构型Fig.8 Buckling configuration corresponding to critical loads

由图7可知,随着管柱上端拉力增加,管柱下端压力逐渐减小,管柱的螺旋角θ也线性减小,但在图中放大位置处,曲线表现出非线性特性,表明发生了刚螺旋的屈曲构型。最后螺旋角突然消失,管柱呈直线状态。阻尼比对刚发生螺旋屈曲有一定的影响,如图中放大部分所示。但整体来看,阻尼比对管柱的螺旋角影响较小,随着阻尼比减小影响也逐渐减小,表明逆向加载法对分析管柱屈曲是可行的。

取阻尼比为1,根据图7的计算结果,图8给出了各种临界载荷对应的屈曲构型图。图8中圆点代表第1接触点,三角代表第2接触点,管柱下端部与第1接触点之间为第1非接触段,第1接触点和第2接触点之间为第2非接触段,管柱上下端的第2接触点之间为连续接触段。

由图8可见,当ξL=8.67时,俯视图的屈曲构型中第2接触点重合,螺旋角正好360°,管柱发生了以第2接触点度量螺距的螺旋屈曲,此时第1接触点之间的螺旋角为467.8°,见图8(b);当ξL=7.38时,俯视图的屈曲构型中第1接触点重合,螺旋角正好360°,管柱发生了以第1接触点度量螺距的螺旋屈曲,此时第2接触点之间的螺旋角为262.9°,见图8(c);当ξL=4.06时,管柱刚发生螺旋屈曲,管柱挠曲线为空间三维曲线,与井筒存在2处接触,接触点之间的螺旋角为82.7°,见图8(d);当ξL=1.91时,管柱发生正弦屈曲,管柱挠曲线为平面曲线,与井筒存在1个接触点,见图8(e)。

取不同的阻尼比,各阶屈曲模态的无因次临界载荷见表1。由表1可知,阻尼比0.75≤ζ≤24.0时,阻尼比对各个临界载荷的影响甚微,逆向加载法得到的临界载荷与正向加载法结果的最大误差为1.55%,而与黄文君等[23]理论解的最大误差为2.77%。另一方面,正弦屈曲临界载荷与Lubinski等[1]的解析解1.94更接近,说明逆向加载法的方法是合理的,同时表明计算精确度较高。

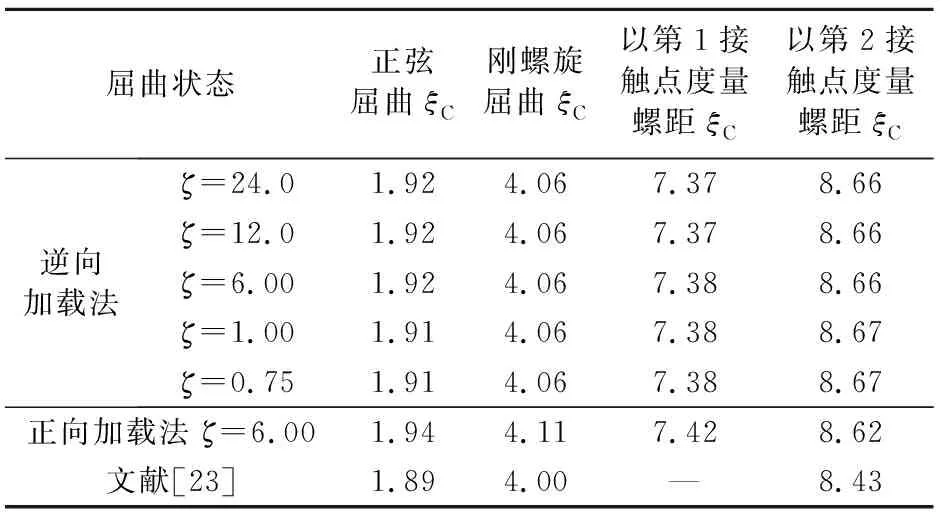
表1 屈曲无因次临界载荷对比

3.4 管柱长度对临界载荷影响

图9给出了不同管柱长度条件下螺旋角随受压载荷变化曲线。在正弦屈曲、刚螺旋屈曲、以第1接触点和第2接触点度量一个完整螺距的屈曲条件下,图10给出了随管柱长度变化的挠曲线。

由图9可见,在同一个受压载荷作用下,管柱越长,对应的螺旋角越大,表明达到同一个螺旋屈曲状态时,对应的临界载荷也越小,例如以第1和第2接触段度量螺距便是这种情况。刚螺旋屈曲和正弦屈曲时,管柱越长对应的临界载荷也越小。其中螺旋向正弦屈曲构型转变是一个突变的过程。

由图10可见,在同一种屈曲构型中管柱下端的挠曲线基本一致。随着管柱长度增加,从受压段到受拉段,管柱挠度逐渐趋于0,表明受拉段对螺旋屈曲的构型有影响;但是,随着管柱长度增加,受压段屈曲后的挠度趋于相同,也表明受拉段对螺旋屈曲受压段长度的影响是有一定限度的。

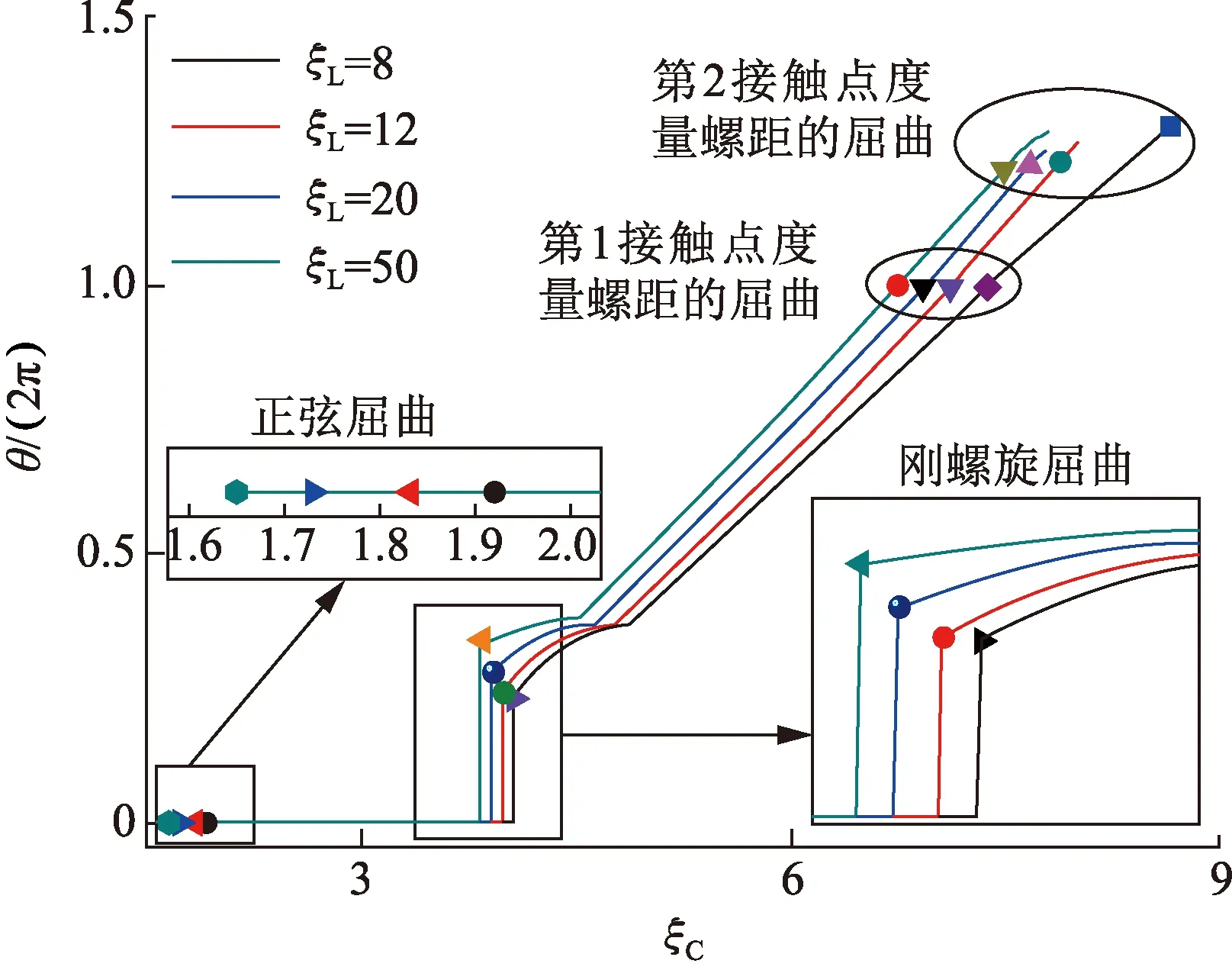
图9 螺旋角随受压载荷变化曲线Fig.9 Change of helix angle with compression load

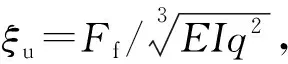
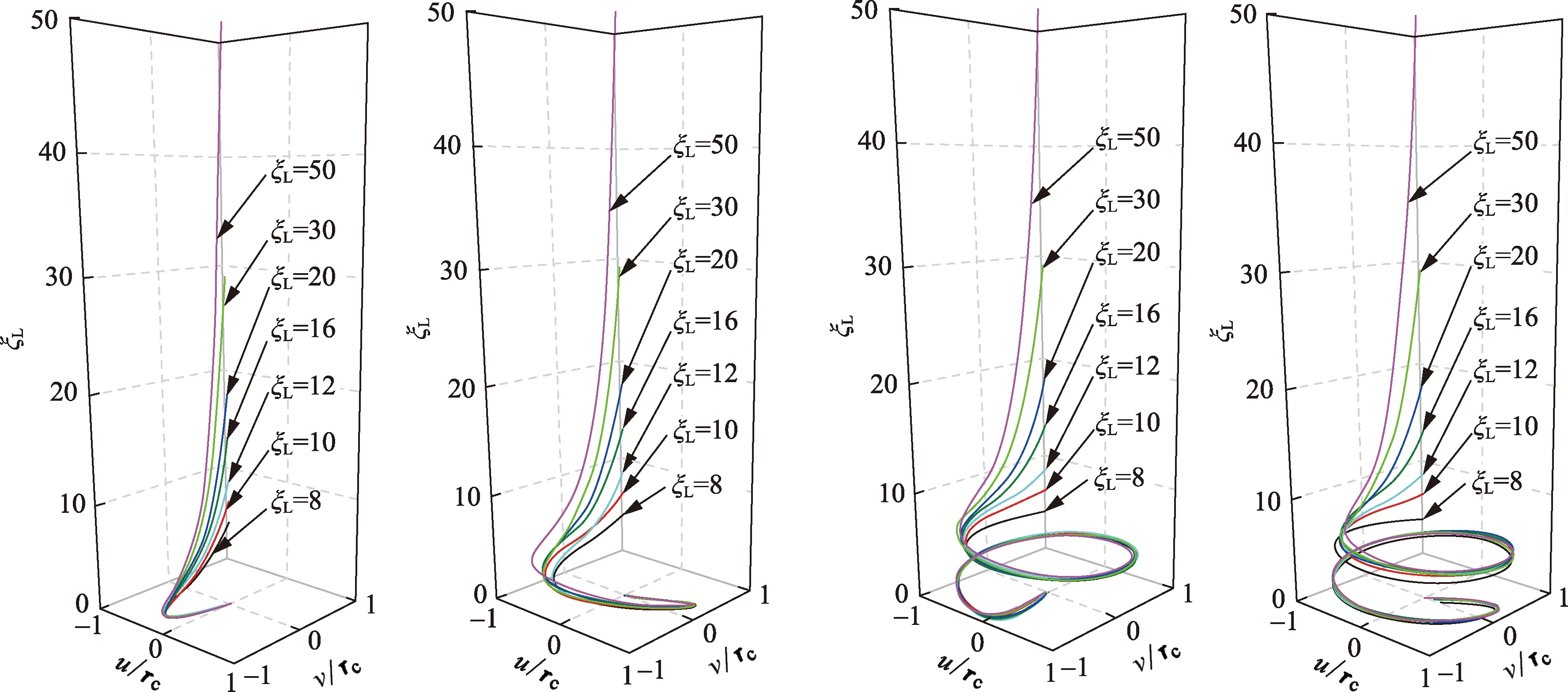
图10 随管柱长度变化的挠曲线Fig.10 Deflection curve with tubing length changing

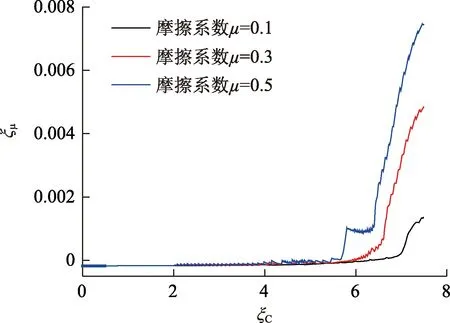
图11 不同摩擦系数下管柱摩擦力随受压载荷曲线Fig.11 Change of friction force with compression load at different friction coefficient

在正弦屈曲、刚螺旋屈曲、以第1接触点和第2接触点度量一个完整螺距条件下,图12给出了临界载荷随管柱无因次长度曲线。由图12可见,随着管柱无因次总长度增加,无因次临界载荷均逐渐减小并趋于常值。管柱无因次总长度8≤ξL≤50时,正弦屈曲无因次临界载荷ξC从1.92减小到1.65,见图12(a);刚螺旋屈曲的无因次临界载荷ξC从4.06减小到3.84,见图12(b);以第1接触点度量螺距的无因次临界载荷ξC从7.37减小到6.75,见图12(c);以第2接触点度量螺距的无因次临界载荷ξC从8.65减小到7.48,见图12(d)。

无因次总长度ξL从8增加到30时,这4种屈曲构型的无因次临界载荷分别减小了13.02%、5.17%、7.19%和12.14%,无因次总长度ξL从30增加到50时,对应的临界载荷分别减小了1.20%、0.26%、1.32%和1.58%,进一步表明随着管柱总长度增加,其临界载荷逐渐减小并趋于常值。

根据图12的载荷曲线,利用Origin软件中的Logistic函数,进行多项式曲线拟合,拟合具有较高的吻合度。得到的无因次临界载荷的拟合公式为

ξC=A+(B-A)/[1+(ξL/E)F], 8≤ξL≤50.

(12)

式中,A、B、E和F为拟合系数,表2给出了拟合公式及其各项系数。

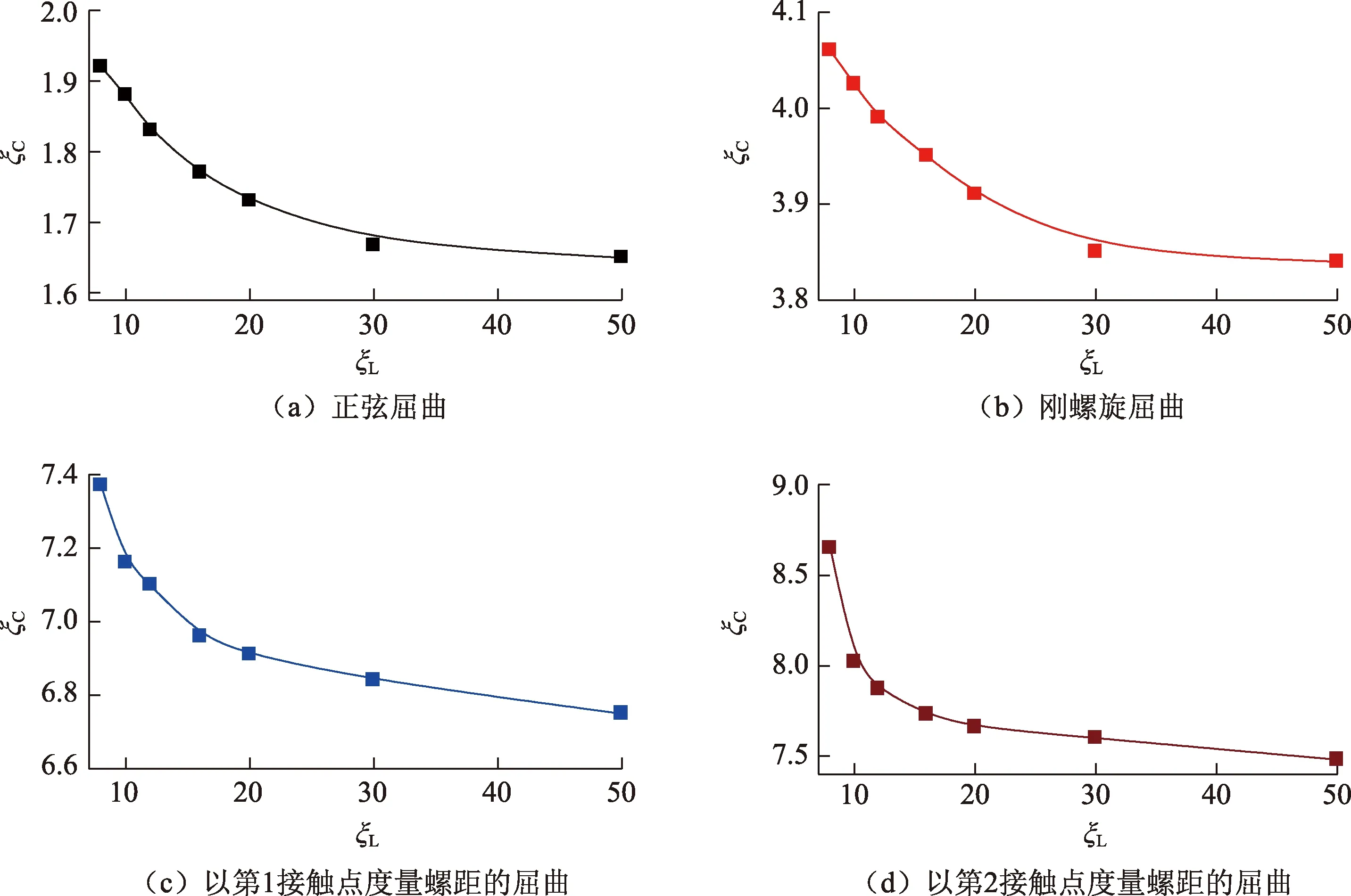
图12 管柱长度对临界载荷影响Fig.12 Effect of tubing length on critical load

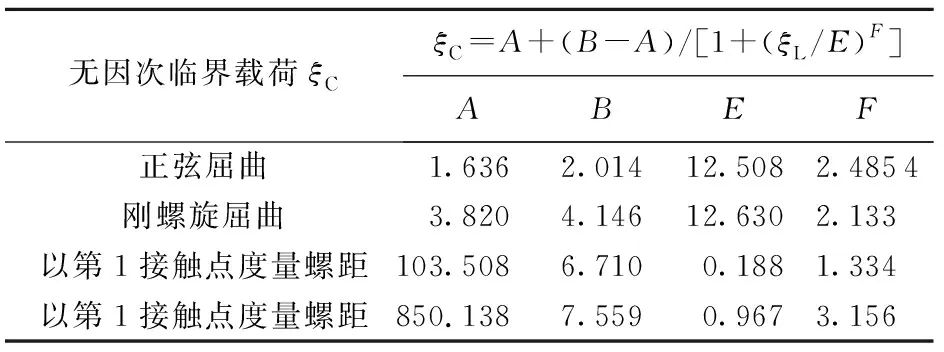
表2 无因次临界载荷的拟合公式

在工程应用中,根据式(1)将管柱的总长度L进行无因次化,由于临界载荷随管柱长度的增加而逐渐减小,并趋于常值,如果无因次总长度ξL大于50,取ξL=50时的ξC。按照式(12)进而得到管柱正弦屈曲、刚螺旋屈曲、以第1接触点和第2接触点度量一个完整螺距条件下的无因次临界载荷ξC。

由于摩擦力对临界载荷影响甚微,qL≅FT+FC,可求出临界载荷对应的井口悬挂拉力FT,表示为

(12)

当井口悬挂拉力大于FT时,管柱在井底受压段不会发生相应的屈曲变形。

4 结 论

(1)提出的逆向加载法中,根据正向加载得到的稳定螺旋屈曲构型,逐渐增大悬挂拉力,从而减小了管柱的井底压力,得到了相继发生以第2接触点和第1接触点度量一个完整螺距的屈曲、刚螺旋屈曲和正弦屈曲的各阶屈曲模态构型。其中形成完整螺距的屈曲和正弦屈曲过程的螺旋角与井底压力为线性关系,只有2接触点的刚螺旋构型的螺旋角与井底压力呈现出非线性特性,螺旋屈曲构型向正弦屈曲构型转变是一个突变的过程。

(2)摩擦力对临界载荷的影响甚微。随着管柱无因次总长度增加,各阶屈曲模态的无因次临界载荷均逐渐减小并趋于常值。