风载荷作用下的操纵性研究

魏可可，高霄鹏

(海军工程大学 舰船工程系，湖北 武汉 430033)

0 引 言

早期，对船舶的航行性能研究主要侧重于静水中，随着对海洋不断的探索，船舶在海面上航行的时间大大加长，偏离海岸的距离也越来越远，带来的便是经历的海况更加复杂，船舶受到较小的风载荷便会发生横向的漂移、航向位置改变等现象，特别是在大风和复杂海流的海况下，当船舶操纵性能不佳或者操纵不当很有可能使船舶发生倾覆和碰撞的危险，因此，考虑风载荷作用下的操纵性预报研究也越来受到重视。

国内对于风载荷的数值计算以及考虑风载荷作用下的操纵性理论预报研究不多，且研究时间较晚，朱齐丹等[1]通过基于一种上下界的滑模控制方法，考虑外界风浪流对某欠驱动船模的干扰影响，对有无干扰的欠驱动船模分别进行数值仿真，进而探讨了风浪流对其操纵运动干扰的影响。吴秀恒等[2]应用流体力学、参数辨识等方法，探索出了不同水深情况下船桨舵四象限水动力及其干扰系数和风浪流对船舶作用力的计算公式，从而对某船考虑了风浪流作用下的操纵性进行预报研究。田超[3]采用OpenGl 虚拟现实仿真技术，基于MMG 操纵性运动方程，对考虑了风浪流因素下船舶的操纵运动进行数值计算。吉春正[4]以某滑行艇模型为研究对象，选取定常风、规则波和均匀流的数值计算工况，分别求解了风、浪、流的干扰力，并将其叠加到静水操纵性运动方程中，从而确定了风浪流载荷作用下滑行艇操纵运动数学模型，对风浪流干扰下滑行艇的操纵性作了预报。

国外对于风载荷的计算研究较早，已经形成了一系列的理论和数值模拟方法，且这些理论和数值模拟方法能较为准确地计算出风流载荷系数。同时对于考虑风流载荷作用下船舶的操纵性预报研究也早于国内，通过长期的试验[5-8]形成了一整套计算方法。Xue,Y 和Lee, BS 等[9]以某港口船舶为研究对象对其进行三自由度建模，考虑了对作用该港口船舶上的风浪流干扰并对风浪流的力和力矩进行数值计算，最后对港口船进港时的操纵性作了数值预报。Fahd Fathi 等[10-14]对LNG 船进行CFD 数值模拟,通过改变网格划分条件、边界条件、湍流模式等因素对该船型的流载荷进行数值模拟计算，发现风载荷对LNG 船的运动响应有着重要的影响。Fujiwara T 等[15-16]长期从事对FLNG 和LNG 船的操纵性研究，基于风洞实验提出对FLNG 和LNG 船的风载荷估算方法，并对该船型在特定海况下的操纵性指标做出了评估。Raman-Nair, W 和Gash, R 等[17]构造了含有风、流、桨、舵等影响因素项的操纵性方程，通过基于Matlab 平台采用龙格-库塔法求解该操纵性方程，研究了风载荷和流载荷对某船航向控制的影响。

大多数学者侧重于风浪流联合作用时对操纵性的影响研究，其中对单独考虑风载荷操纵性预报的研究较少。本文以某水面舰船为研究对象，构造考虑风载荷作用下的三自由度MMG 操纵性方程，从而实现风载荷作用下该船舶的操纵性预报，为工程应用提供一定的借鉴。

1 操纵性运动模型

1.1 常规的MMG 操纵性运动方程

MMG 操纵性方程是一个通用的方程。该方程分别单独考虑船、桨、舵的水动力及其之间的相互干扰，方程的具体形式如下式：

式中：下标H，P，R 分别为船，桨，舵；X，Y，Z，L，M，N 分别为纵向力，横向力，垂向力，横摇力矩，垂荡力矩以及转首力矩；为船舶的质量；分别为船体坐标系轴，轴以及轴的附加质量；分别为船舶的航速在船体坐标系轴，轴以及轴方向上的分量；分别为船舶绕船体坐标系轴，轴以及轴的转动角速度；为为船舶绕船体坐标系轴、轴以及轴的自身质量惯性矩。

本文以某双桨双舵的水面船模为研究对象，对其操纵性进行研究，考虑船、桨、舵之间的干扰效应，因而采用MMG 操纵性方程。该船在静水面作操纵运动，其升沉、纵倾和横倾很小，可忽略升沉、纵倾和横倾对水平面内运动的影响，因而采用式（2）所示的三自由的MMG 操纵性方程可对其静水操纵运动进行研究。

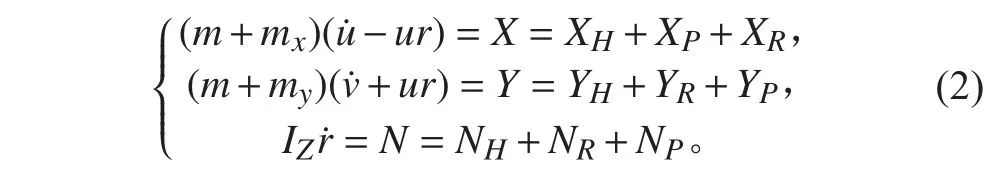
1.2 风载荷作用下的操纵性方程

对于考虑风载荷作用下的操纵性方程的构建，只需在方程中加入由风载荷引起的力和力矩即可。在原有的三自由度MMG 操纵性方程中等式的右边叠加风载荷的力和力矩，其中主要是风载荷对船舶的纵向力横向力 YWind以及转首力矩从而可得到风载荷单独作用时的三自由度MMG 操纵性方程如下式：

2 静水中操纵性预报与验证

基于Matlab 软件平台采用三自由度的MMG 操纵性方程对静水中水面船模的操纵性进行了数值理论预报，其中水动力系数以及船桨舵的水动力、附加质量可以参考文献[18]求解。

2.1 静水中的回转运动

静水中的回转运动采用的航速V=1.38 m/s、分别选择右舵为15°，25°，35°等舵角的工况进行数值模拟。分析了每个工况下的无因次回转轨迹的时历曲线，并与试验值进行对比，如图1 所示。

图 1 不同舵角无因次回转轨迹与试验的对比Fig. 1 Comparision of dimensionless rotating track to experimentation with different rudder

由图1 可知，无因次定常回转直径在舵角为15°时大于试验值；当舵角为25°时无因次回转轨迹基本与试验值吻合，因此其无因次定常回转直径很近；而在舵角为35°时，无因次定常回转直径要小于试验值。

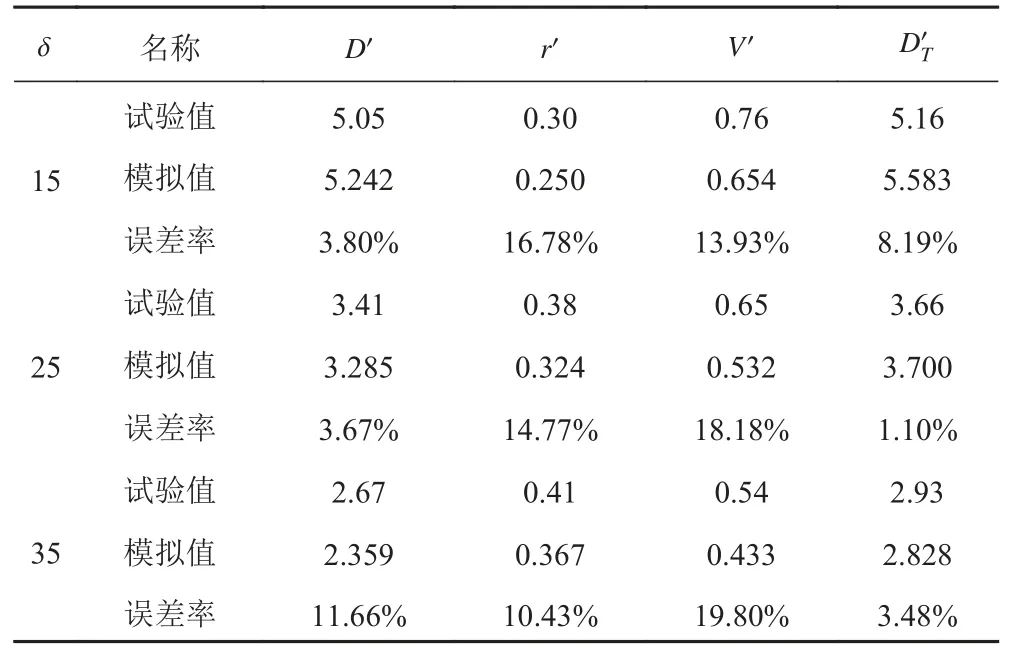
表 1 回转运动中特征参数的结果对比Tab. 1 Comparison of the turning motion characteristic parameters

2.2 静水中的Z 形运动

对于Z 形运动，选取航速V=1.38 m/s 和舵角及首向角为+10°/+10°，+20°/+20°的工况进行数值模拟。分析每个工况下的初转期超越时间第一超越角第二超越角等Z 形运动的特征参数值，并与试验值进行对比，如图2 所示。

图 2 不同舵角与首向角时历曲线的对比Fig. 2 Comparision of the time curve with different rudder angle and course angle

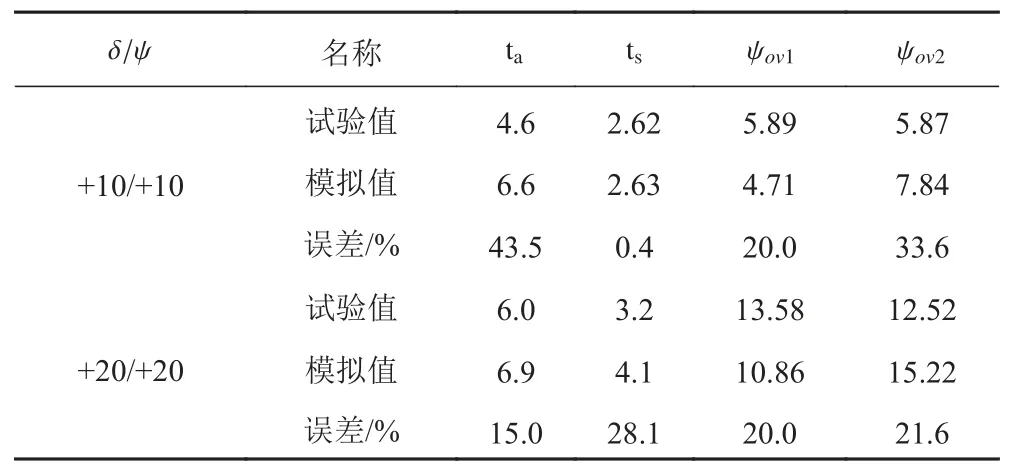
表 2 Z 形运动中特征参数的结果对比Tab. 2 Comparison of the Zigzag motion characteristic parameters

由图2 可知，静水中数值预报的舵角和首向角的时历曲线与试验时的时历曲线相比差别较大，其中周期、第一超越角和第二超越角等Z 形运动的特征参数值都要比试验值大。

由表2 可知，当舵角和首向角为+10°/+10°时，初转期的误差较大为43.48%；超越时间的误差为0.38%；运动周期误差也较大为31.18%；第一超越角和第二超越角的误差分别为20.03%和33.56%。由此可见，除了超越时间的误差较小外，其他特征参数的误差都较大。当舵角和首向角为+20°/+20°时，初转期的误差为15.00%；超越时间的误差为28.13%；运动周期误差为18.63%；第一超越角和第二超越角的误差分别为20.03%和21.57%；在该舵角和首向角下，数值计算的特征参数误差都较大，超过了15.00%。

通过对静水中回转和Z 形的理论预报，并与试验值进行对比，虽然存在一定的误差，预报的结果还是达到了一定的精度，证明该理论预报方法具有可行性，可以运用该方法对风载荷作用下的操纵性进行预报研究。

3 风载荷作用下的操纵性预报

根据风洞试验所得风载荷，将其叠加到三自由度的MMG 操纵性方程中，从而实现对考虑有风载荷的该水面船模的操纵运动进行数值理论预报。通过与静水中无风载荷的操纵性预报进行对比分析，可以研究和探索风载荷对该水面船模的操纵性的影响。

3.1 风载荷作用下的回转运动

由图3 和图4 可知，由于增加了风载荷这个外载荷扰动量，无论舵角为15°，25°还是35°，预报的无因次回转轨迹都发生了一定扰动变化，呈现螺旋状的回转，并且无因次定常回转直径都要小于静水中预报值。静水中预报的航速出现了2 次速降的过程，而风载荷作用下的航速只有一次速降的过程，且受风载荷的作用航速最终也是呈现波动变化的。

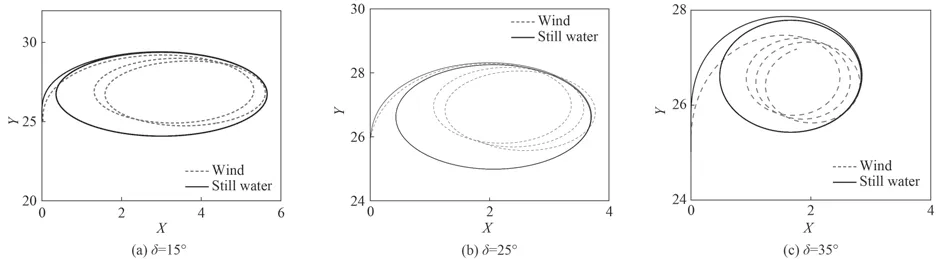
图 3 不同舵角下无因次定常回转轨迹的对比Fig. 3 Comparision of dimensionless rotating track with different rudder angle

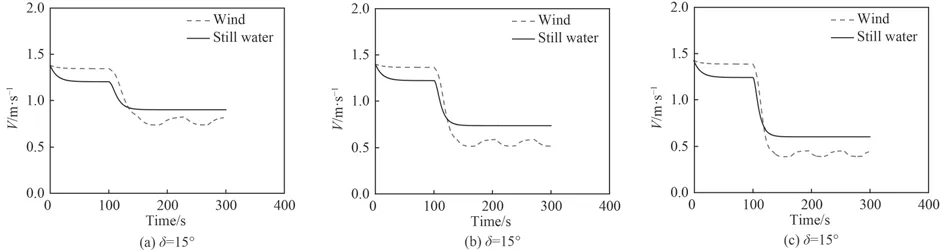
图 4 不同舵角下航速的对比Fig. 4 Comparision of velocity with different rudder angle

3.2 风载荷作用下的Z 形运动

对考虑风载荷作用下的Z 形运动，选取航速V=1.38 m/s、风速=4.86 kn、舵角和首向角为+10°/+10°和+20°/+20°的工况进行数值模拟。图5 和图6 分别给出了风载荷中和静水中的舵角与首向角的时历曲线对比和航速的对比。

图 5 不同舵角与首向角时历曲线的对比Fig. 5 Comparision of the time curve with different rudder angle and course angle

图 6 不同舵角和首向角航速的对比Fig. 6 Comparision of velocity with different rudder angle and course angle

由图5 和图6 可知，对于考虑了风载荷的Z 形运动，所求的舵角和首向角的时历曲线、航速等与静水中的仿真值相比，都发生了较大变化。其中，舵角和首向角的时历曲线中的周期、超越角等特征参数都要大于静水中的所对应的仿真值；航速的变化规律基本与静水中仿真值一致，但其峰值的波动较静水中更厉害。

3.3 对比分析

3.3.1 回转运动

图7 分别给出舵角为15°，25°，35°时的静水、风载荷、流载荷中无因次定常回转角速度、无因次定常回转直径无因次战术直径无因次纵距无因次横距速降等回转运动的无因次特征参数值的对比条形图。

3.3.2 Z 形运动

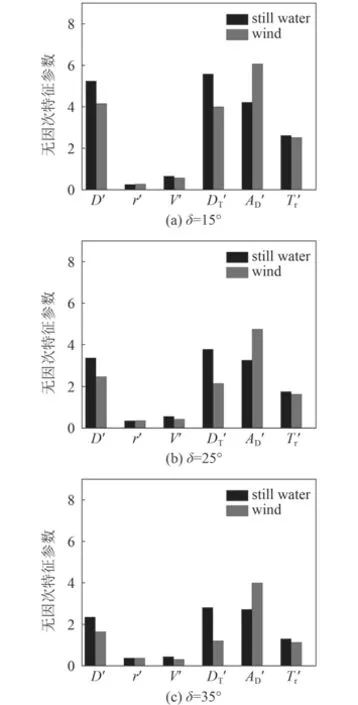
图 7 不同舵角无因次回转特征参数的对比Fig. 7 Comparison of dimensionless rotary characteristic parameters with different rudder angle

图 8 不同舵角和首向角Z 形特征参数的对比Fig. 8 Comparision of zigzag characteristic parameters with different rudder angle and course angle

图8 分别给出舵角和首向角为+1 0°/+1 0°和+20°/+20°时的静水、风载荷中初转期超越时间第一超越角第二超越角等Z 形运动的特征参数值的对比条形图。

4 结 语

1）基于三自由度的MMG 操纵性方程，对静水无风载荷的操纵性进行了数值理论预报，并与试验结果进行了误差对比分析，验证了该理论预报方法的可行性；

2）构建考虑风载荷的三自由度MMG 操纵性方程，对考虑风载荷的操纵性也进行了数值理论预报，并与静水中的理论预报值进行了对比。研究发现，对于回转运动，无因次回转直径、无因次战术直径、速降、无因次横距等回转运动参数都要小于静水中理论预报值，回转角速度基本与静水理论预报值一致，无因次纵距要大于静水中的理论预报值；而对于Z 形运动，初转周期、超越时间、第一超越角以及第二超越角等Z 形运动参数都要大于静水中理论预报值，由此可知风载荷对该水面舰船的操纵性有一定的影响。