基于在线鞍点优化算法的博弈决策求解研究
许 月,谢 歆
(1.安徽理工大学 数学与大数据学院,安徽 淮南 232001;2.黄山学院 数学与统计学院,安徽 黄山 245041)
经济博弈[1]最具代表性的市场结构是寡头垄断。它是少数几家大厂商占整个行业的绝大部分产量,并且相互依赖。所有厂商均在假定竞争对手行为最优条件下,采取使自己收益最大化的策略,来达到寡头垄断市场的均衡——纳什均衡[2]。纳什均衡所对应的一组决策,称为纳什均衡点,它是衡量博弈网络中稳定的一个重要标准。
通过鞍点优化方法[3]在经济博弈中找到纳什均衡[4-5],是一条新蹊径。鞍点方法是一种原始对偶方法,通过交替更新决策变量(原变量)和拉格朗日乘子变量(对偶变量)有效地处理优化问题的等式或不等式约束:

式中:xt和λt是第t次迭代的原变量和对偶变量;∇xL(xt,λt)和 ∇λL(xt,λt)表示对函数L(xt,λt)分别求x和λ偏导;αt为迭代的步长;PX表示将值[xt-αt∇xL(xt,λt)]投影到集合X上,其中X={x1,x2,…,xT};[·]+为取正实数。运用鞍点方法的思想,找出一组原变量和对偶变量(x,λ),其中x和λ依据在线梯度下降法更新迭代。而[6]是在[3]的算法基础上证明该算法的遗憾界不大于(T为迭代次数)[6]。不同的是,SP-FTL(saddle-point follow-theleader)[7]算法是求解经过拉格朗日对偶变换的回报函数累计和的鞍点值,即纳什均衡点作为这个“leader”来进行 (x,λ)迭代,并且验证了 SP-Regret和Ind-Regret不能同时达到次线性遗憾。跟随领导者算法(FTL)决策更新依赖于初始“leader”,算法如下:

其中:xt+1表示t+1时刻的决策变量;τ为[1,t]之间的时间变量;表示总收益函数。
在[7]的基础上将SP-FTL算法应用经济博弈中,并且加上正则化项以达到稳定决策的目的。由于在线凸优化算法[8]只涉及一个优化对象,而在线鞍点优化涉及两个如(1)式的(x,λ),所以在线凸优化框架可以看作是在线鞍点问题的一个特例。不仅如此,将上述鞍点优化算法置于在线环境[9]下,得到算法OSP-RFTL(online saddle-point regularization follow-the-leader),并验证了算法的有效性。为了进一步模拟真实的经济网络,需要考虑存在一些不稳定因素,如Byzantine故障,完全垄断市场的厂商被看成是破坏纳什均衡的Byzantine故障[10](即恶意攻击点)。其原始问题是Byzantine将军问题:爱国的将军为不被叛国将军破坏行动而要达成一致。Byzantine容错的目的是能够抵御故障,在满足整个经济市场稳定的同时允许出现这样带有攻击性的厂商最大数量。
1 问题建立
问题一:鞍点优化算法与博弈决策选择的等价性建立。
定义由{1,2,…,N}个体构成的多个体网络[11],这些个体在寡头垄断的经济市场下视为竞争厂商,选择满足纳什均衡的决策:

其中:xt+1,yt+1分别表示在t+1时刻原变量和对偶变量;表示累积收益。为使得整个网络稳定,每次的决策希望能够在给定的范围内波动。
问题二:优化算法性能的衡量。
鞍点遗憾RgtSP表示累积收益与总收益函数的差值,其最小化定义为

在线鞍点问题的目标是共同选择双方的决策,使双方的收益都接近纳什均衡。此外,当一次只优化一方的收益时,标准的在线凸优化环境适用于在线鞍点问题。具体来说,将双方的个人遗憾定义为:
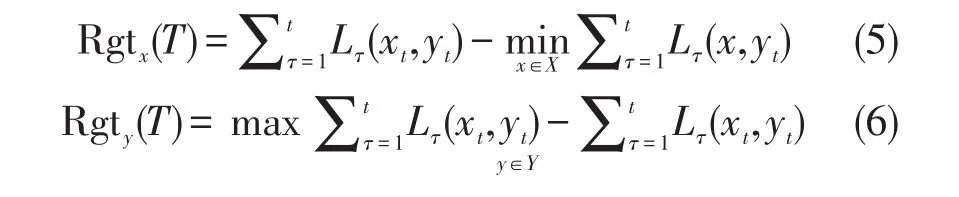
本文的目标是在每次迭代中为双方共同选择一组决策,使每一方在最后的累积收益尽可能接近于总博弈的纳什均衡(即鞍点)。
问题三:算法推广到Byzantine环境下应用目的。
当寡头市场中出现敌意厂商,政府如何及时有效地介入市场控制垄断现状呢?
2 算法介绍
2.1 预备知识
若函数L(x,y)是凸-凹的,X={x1,x2,…,xT},Y={y1,y2,…,yT}对任何原变量x∈X和对偶变量y∈Y,收益函数L的鞍点(x*,y*)满足

若f是关于X→R的H-强凸的,有下列式子成立:

这里,∇f(x)表示f在x处的次梯度。强凸性意味着最小化问题f(x)有唯一解。同样地,如果L是H-强凸凹的,那么存在唯一鞍点(x*,y*)。
2.2 假设条件
假设1 个体所在网络由{1,2,…,N}构成的全耦合网络。
假设2 {Lt,(p,q)(x,y)}为个体p与q在t时刻的收益函数,x,y分别为p和q对应的决策变量,p,q∈(1,2,…,N)且(p,q)=(q,p),p≠q。{Lt,(p,q)(x,y)}是一系列H-强凸凹的并且满足G-Lipschitz的函数。
假设3 为了阻止厂商的恶意计划,所有厂商都直接相互交换信息。
2.3 在线鞍点FTL算法
OSP-FTL依据以下规则进行迭代更新:
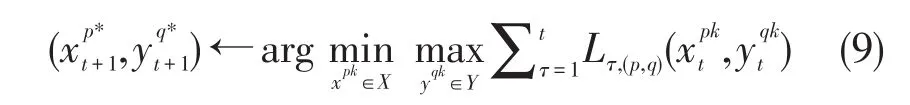
2.4 FTL算法——决策正则化
令决策变量x∈[-1,1],,并且对对迭代次数τ=2,…T时,让fτ在-x和x间交替变换。因此,

可以看出决策将在xt=-1和xt=1之间变化,这样的决策是不稳定的。修改FTL方法,引入正则化[8],使其不会频繁改变决策,从而降低的遗憾。
OSP-RFTL依据(11)式进行迭代更新
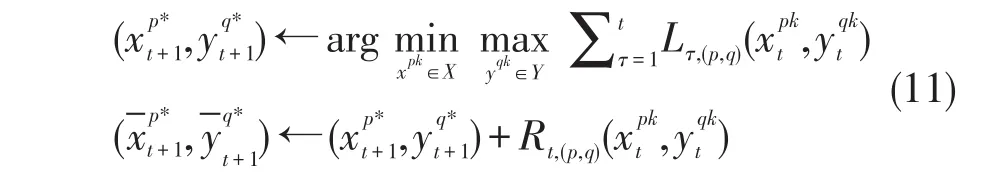
2.5 OSP-RFTL算法的应用
2.5.1 Byzantine容错思想的引入
如图1,恶意节点C给A发送值9,给B发送值12,A计算中位数{9,10,11}=10,B计算中位数{10,11,12}=11,C的攻击行为导致A,B计算结果不一致。若有f个厂商想要垄断,能使得市场处于均衡状态的总厂商数量是未知的。
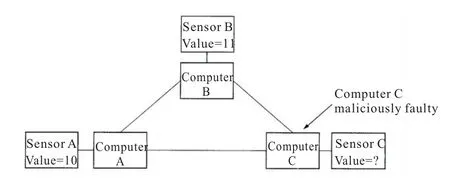
图1 节点交流输出中位数
2.5.2 3f+1容错思想在政府反垄断中的应用
为了容纳一个错误结点,不防设个体1为恶意结点,总共有4个结点,如图2。个体1因为共同协议不能满足个人需求,暗自更改决策更新规则。“-”表示表面与其他厂商约定的决策更新规则与背地里的更新规则不一致。
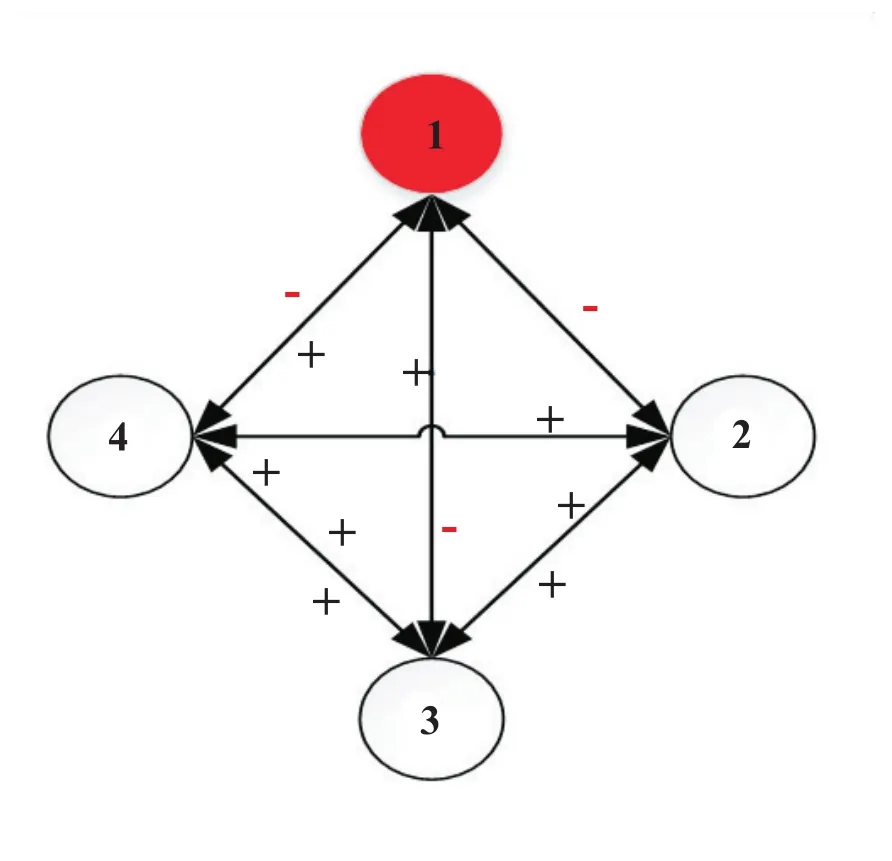
图2 厂商交流网络示意图
2.5.3 OSP-RFTL算法的推广

把意图想要完全垄断市场的厂商看成是有Byzantine故障的(恶意攻击的个体),即上述(12)式的*所表示的含义,*的右边表示的是向量,满足使他个人达到最优情况的集合:要么取得最小值,要么取得最大值。如果该厂商谋取成功,那么当前迭代值取自这样特定的集合的任意值;如果未取得成功,随着时间的推移,厂商将重新回到与其他厂商相互制约的均衡状态。这样就得到了算法BOSP-RFTL(Byzantine online saddle-point regularization follow-the-leader)。具体如算法1。

算法1 BOSP-RFTL算法1:初始化 xt,f=0,[m]2:for t={0,1,…,T}do 3:所有个体对外发送“合作”信号4:for all i∈[m]do in parallel 5:更新xt+1←arg min x max M∑L(x,M),其中M=[m]/i 6:ifL(xt+1)≤ε//判断协议能不能让该厂商满意//若不满意,就会按照自己意愿设定价格7:重新更新迭代规则:xt+1←arg max∑L(xt)8:输出“该个体i攻击点”9:攻击点计数f=f+1 10:else输出“该个体i正常”11:end for 12:if 3f+1≤[m]13:输出经济市场均衡14:else政府需介入进行反垄断操作15:end for
显然,该算法的时间复杂度为O(T)。
3 收敛性分析
验证加入正则化的鞍点遗憾是否仍能达到次线性遗憾界,证明见文献[7]数学归纳法。
引理1

其中,G为Lipschitz连续常数。
定理1

4 仿真实验分析
数值仿真函数如下
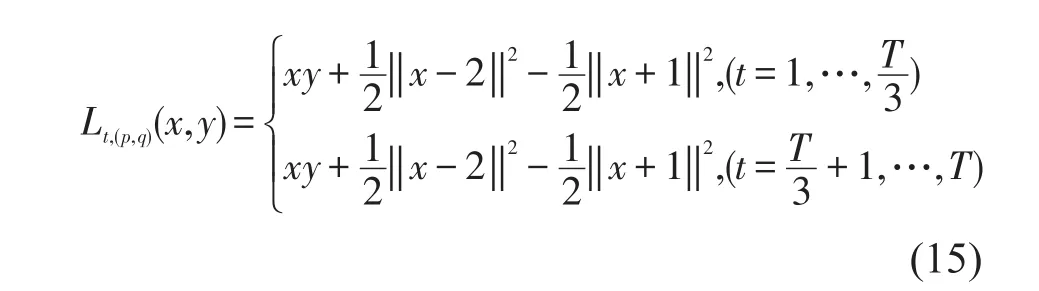
Lt,(p,q)(x,y)表示收益函数,该函数具有时变性。设定迭代次数T,x和y初始状态值从(0,1)随机选取,由t=1开始,x和y根据FTL算法达到鞍点值。
没有加入正则化之前,鞍点优化算法的收敛性为:鞍点遗憾能够达到次线性而有个体遗憾只能够达到线性,如图3。因此,鞍点遗憾和个体遗憾仍不能同时达到次线性。正如公式(11)所示,本正则项R(x,y)=正则化参数用于控制两个目标的平衡关系:在最小化训练误差的同时正则化参数能使模型简单。这里取α1和α2的值为由图4可知,遗憾接近次线性,并且最后能够趋向平稳。
由图5(a)可看出,两个体间的相互决策结果的纳什均衡在不同时刻值都不一样。
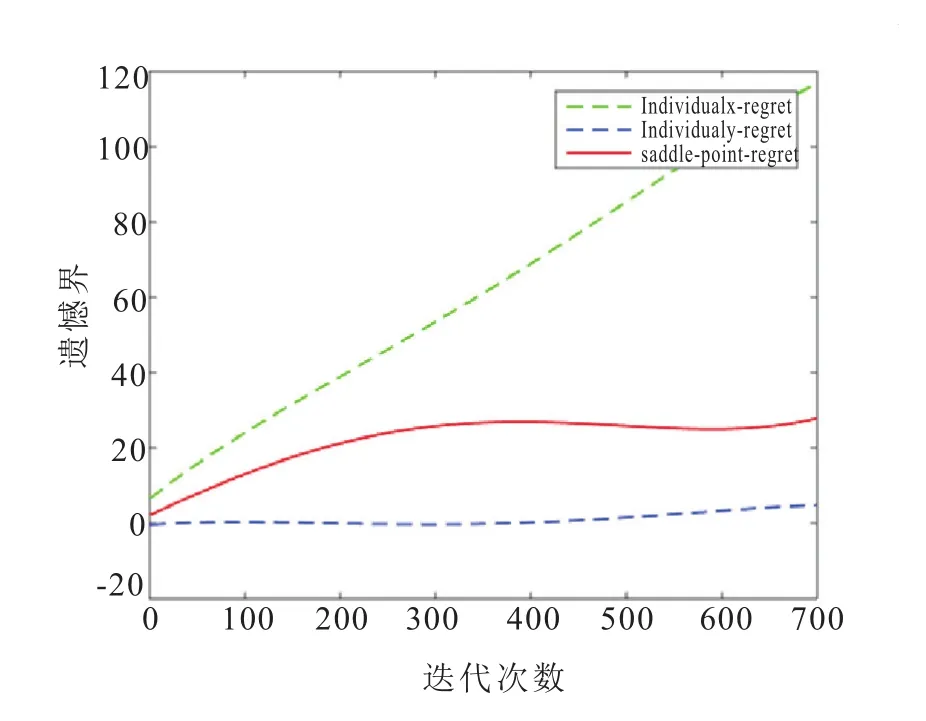
图3 鞍点遗憾和个体遗憾
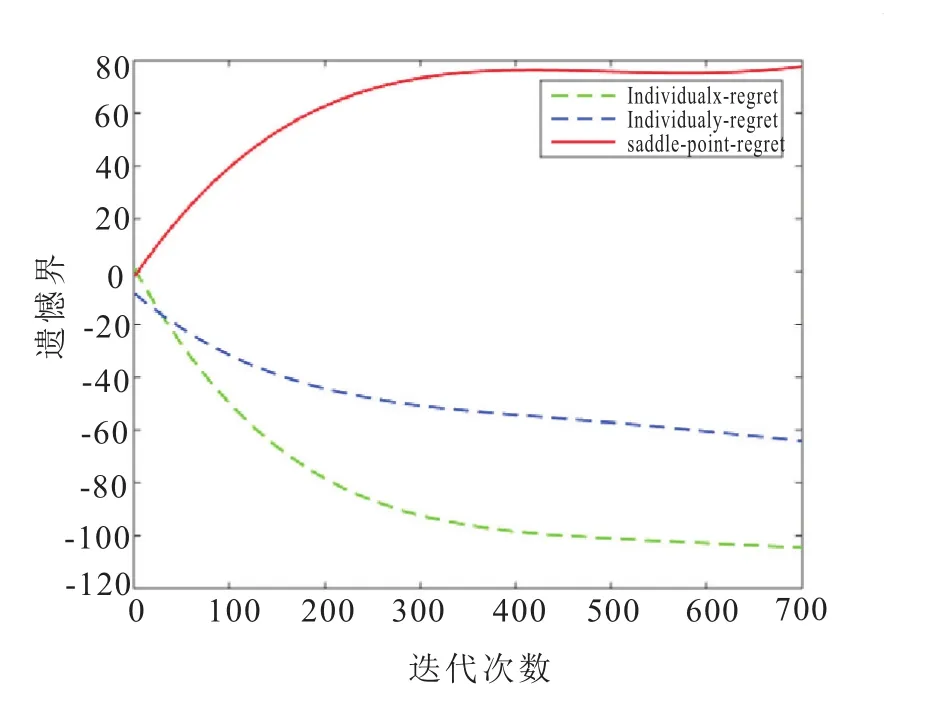
图4 正则化后的遗憾
加入正则化后,相互协商的两个体决策变量稳定在一定的范围内。仿真中给决策x加入0.9倍的L2范数。由图5(b)可以看出,x在值2上下波动。给决策y加入0.1倍的L2范数,同样可看出y在0.6上下波动。这里给出正则项前面不同的系数,以便比较观察正则化的影响。通过加入正则项,纳什均衡可以随着时间推移稳定在一定范围内波动。
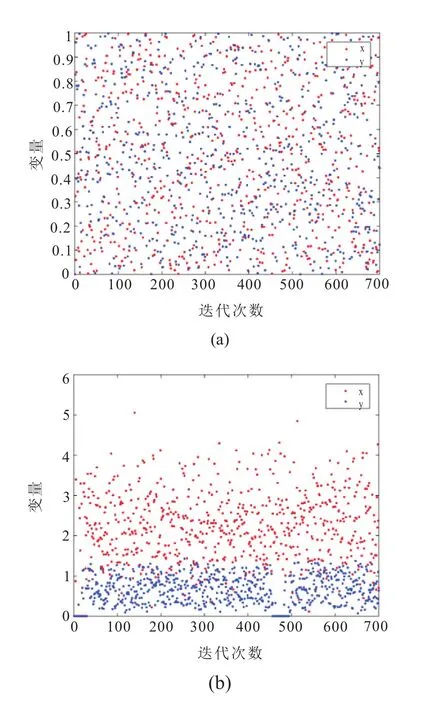
图5 决策状态图 (a)正则化前;(b)正则化后
5 小结
本文把近年来在线鞍点问题的研究成果应用到经济博弈中,提出了追随领导者算法来解决这类决策优化问题,并加入正则化以稳定决策,最后给出了纳什均衡决策的稳定性状态分析,并将Byzantine容错思想应用到政府反垄断实际中。结合近几年来对Byzantine故障容错的研究,3f+1的方法可以更具有弹性,选有检查点[12],没有故障时,只需f+1个结点即可。下一步工作是将算法应用于实际市场,进行有效地监测使用,更好地便于政府反垄断控制。

