一种空谱联合的PCA-LPP高光谱图像特征提取算法

周 敏 ，陆 奎 ，王诗兵

（1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2.阜阳师范大学 计算机与信息工程学院，安徽 阜阳 236037）

高光谱图像分类在精准农业、地质勘测等领域具有重要作用。随着成像光谱仪技术的发展，高光谱图像的光谱分辨率越来越高，数据维度也随之增长，直接使用高光谱数据进行分类容易出现“维数灾难”问题[1]。因此，对高光谱数据进行特征提取是高光谱图像分类的重要步骤。主成分分析（principle component analysis，PCA）方法使降维后数据间的方差达到最大，是对图像的全局信息进行提取[2-3]。局部保持投影（locality preserving projection，LPP）算法能够揭示高维数据中的低维流形结构，挖掘高光谱图像中的局部信息[4]。综合考虑PCA、LPP算法的全局、局部结构保持特性，在各领域的应用中都取得了不错的效果[5-7]。

研究表明，联合使用高光谱图像的光谱特征和空间特征进行特征提取能够获得较好的分类效果[8-11]。Huang等提出基于空-谱距离度量准则的KNN算法进行高光谱图像分类[12]。Hou等在线性判别分析（linear discriminant analysis，LDA）算法的目标函数中引入空间信息参数因子，保留了局部判别信息和图像的空间结构信息，获得了较高的分类精度[13]。因此,本文提出一种空-谱联合的PCA-LPP特征提取算法（spatial-spectral combined pca-lpp feature extraction algorithm，SSPCA-LPP）以提取高光谱图像的鉴别特征。

1 PCA和LPP算法分析

PCA和LPP都是经典的特征提取算法[14]。设原始高维数据集X=[x1，x2，...，xn]∈RK，经投影矩阵W∈RK×k映射后所得的低维数据集Y=WTX，Y=[y1，y2，...，yn]∈Rk（k＜K），k表示选取的主成分个数。

1.1 PCA算法分析

PCA算法通过线性变换去除数据相关性，以投影后的方差最大为优化目标[15]，优化函数

1.2 LPP算法分析

LPP算法通过构造近邻图G来记录像元的局部信息，并使这种近邻关系在投影之后仍得以保持[16]。图G中顶点表示像元，若两像元之间存在近邻关系，则用边将两顶点进行连接，否则，不连接。对图G中任意两点xi，xj之间边的权重

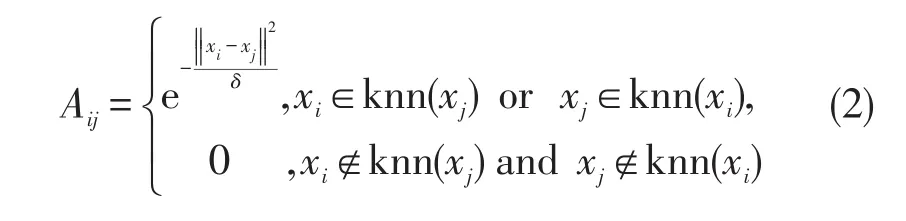
其中，参数δ等于总体样本方差。

LPP算法以最小化近邻像元之间的距离为优化目标[17]，优化函数

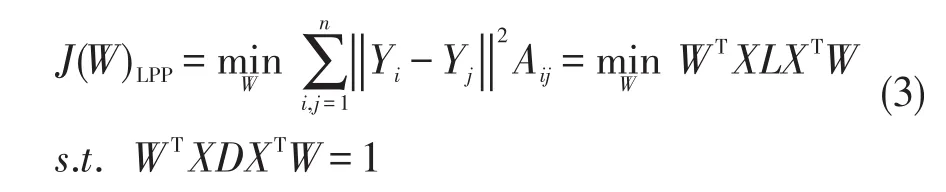
式中，D是对角矩阵，对角元素Dii=∑jAij，L=D-A是Laplacian矩阵。

2 空谱联合的PCA-LPP算法

2.1 空谱重构

空间一致性原理具有明确的物理解释，即在真实地物图像中，同类地物往往具有聚集性，距离越近，属于同类地物的概率越大[18]。设高光谱图像X∈RM×N×B，M×N表示空间大小，B表示光谱维度，像元xij的近邻空间表示为：

Ω(xij)={xpq|p∈[i-a,i+a],q∈[j-a,j+a]}，其中，xpq表示近邻空间中的任一像元，a=(ω-1)/2，ω是空间因子，表示近邻空间的大小，通常取奇数，近邻点个数s=ω2-1。

式中，ωpq=表示近邻空间中任一像元xpq到中心像元xij的权重大小，t是光谱因子，表征不同像元间的影响程度。

重构后的图像中，像元，之间的空-谱距离=‖-。

2.2 空谱联合的PCA-LPP算法

对重构后的高光谱图像数据集使用PCA算法提取全局特征，SSPCA-LPP算法的全局函数

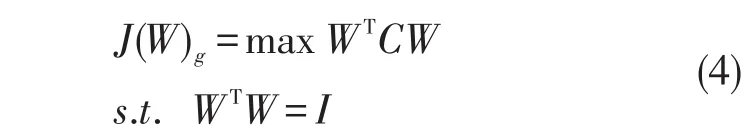
引入光谱信息散度[19]分析近邻像元的相关性，像元越相似，构造近邻图时权值越大。近邻像元、之间的光谱信息散度

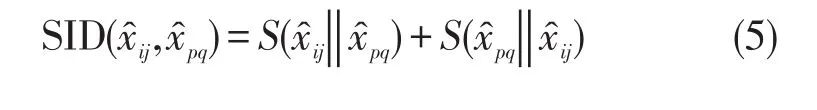
其中

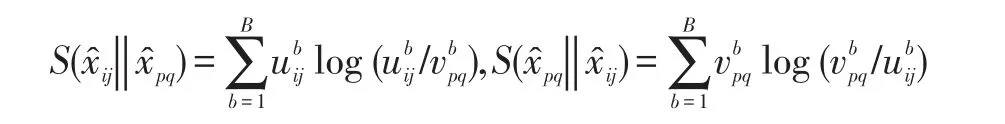
基于空-谱距离度量准则构造局部近邻图，将近邻像元的光谱信息散度作为光谱因子，边的权重计算公式改进

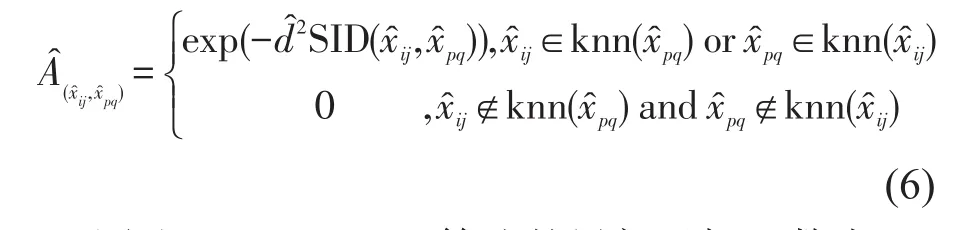
因此，SSPCA-LPP算法的局部目标函数为

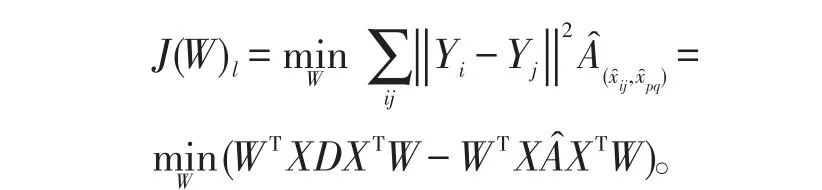
由于约束条件WTXDXTW=I，则上式可转变为求取最大值问题。

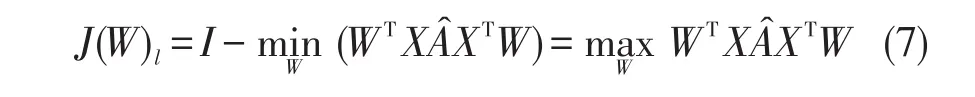
基于最大边缘准则[20]，构建SSPCA-LPP的目标函数

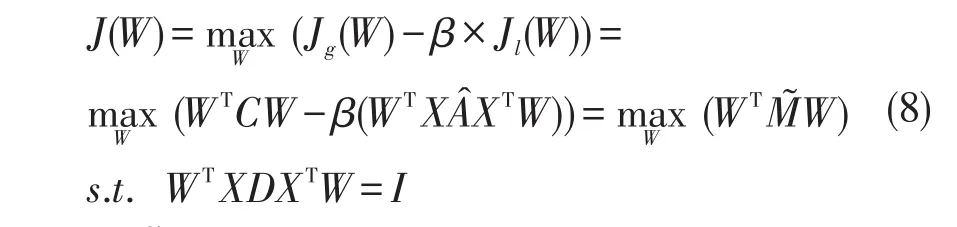
式中，=C+T，β是平滑参数，用于控制局部信息在特征提取过程中的占比。

使用拉格朗日乘子法，将式(8)转化为求解特征值问题。

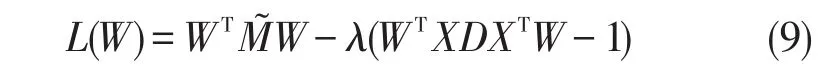
上式对W进行求导并置0，进一步化简可得

选取前k个特征值所对应的特征向量作为主成分分量构成投影矩阵W，得到低维数据。

SSPCA-LPP算法的步骤如下：

输入：高光谱图像数据集X，空间因子ω，平滑参数β，特征维度k。

输出：投影矩阵W，低维数据Y。

Step 1：对原始数据集X进行空谱重构，计算近邻像元的空-谱距离；

Step 3：根据式(8)构造目标函数并计算特征值和特征向量；

Step 4：选取前k个特征向量构成投影矩阵W，得到低维数据Y。

3 实验与分析

3.1 实验数据选择及设置

在Indian Pines公开数据集上，分别使用PCA、LDA、LPP、PCA-LPP、SSPCA-LPP 算法对高光谱图像数据进行特征提取，然后使用SVM算法进行分类。评价指标采用总体精度(overall accuracy，OA)、平均精度(average accuracy，AA)和 kappa系数。

实验中，训练样本和测试样本按比例随机选取，不同算法的影响参数均调整到最佳值，各算法统一提取30维特征，LDA算法提取c-1维（c是地物类别数）[21]。为保证算法的客观性，以下实验数据均为10次实验结果的平均数。

3.2 Indian Pines数据集实验结果及分析

影响SSPCA-LPP算法的主要参数是ω和β。从数据集中随机选取5%的样本作为训练集进行实验。当检验ω对分类精度的影响时，β的值设置为0.3；当检验β对分类精度的影响时，ω设置为7。图1是ω和β对分类精度的影响。

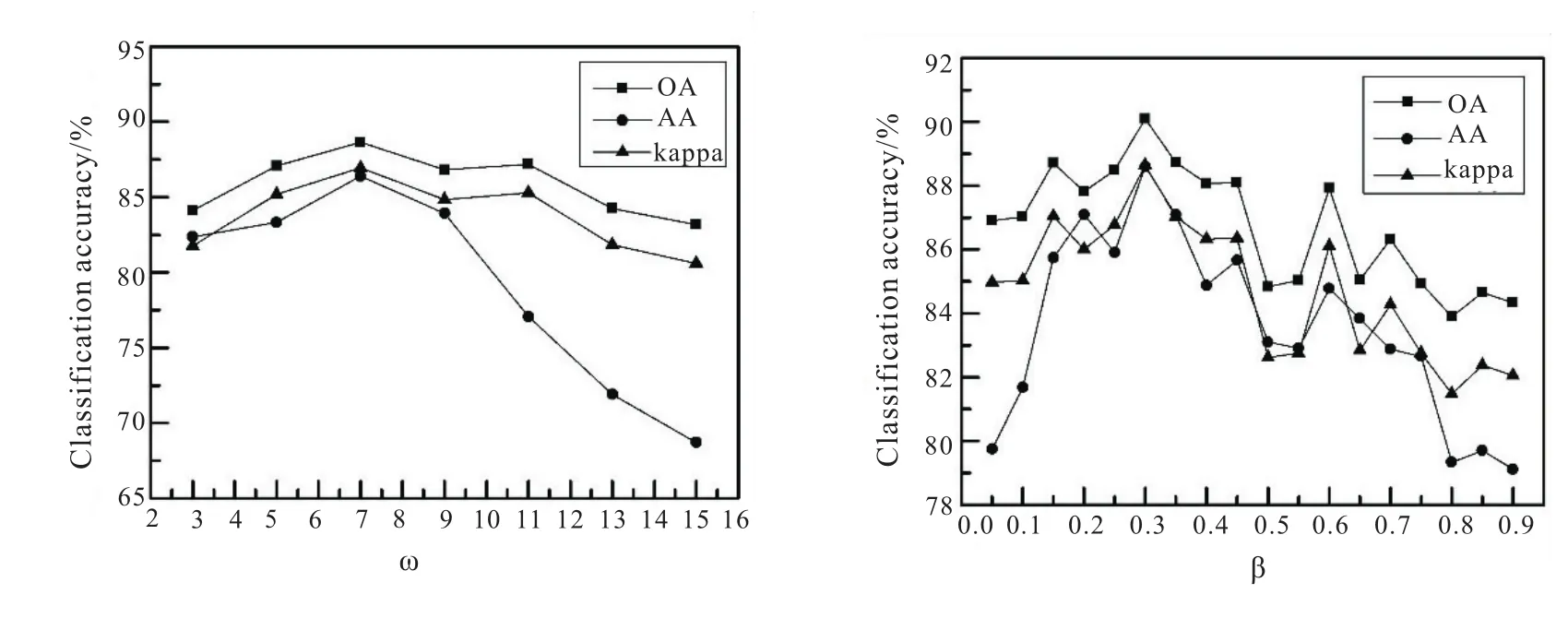
图1 Indian Pines数据集上ω和β对分类精度的影响

分类精度在ω=7，β=0.3处取得最高。当ω＜7时，ω越大意味着近邻区域包括的像元越多，从而能够更好地利用像元的空间信息；当ω＞7时，近邻区域中包含异类像元，导致分类精度下降。同样，β越大表明可利用的局部信息越多，突出了局部信息在分类中的贡献率，但当大于最佳值时，局部信息过于突出，反而忽略了全局信息。

从每类中随机选取5%、10%、15%和20%的样本作为训练集（样本数不足100的类别统一选取10个样本作为训练集），剩余d的为测试集。使用不同算法对高光谱图像进行特征提取并分类，不同算法的分类结果如表1。

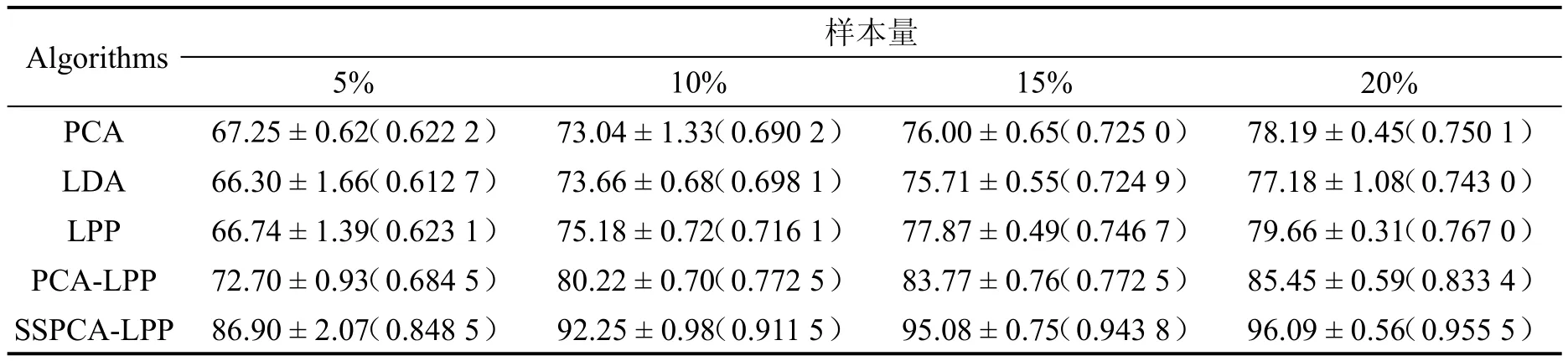
表1 不同算法在Indian Pines数据集上的分类结果(总体精度±标准差(kappa系数))

从表1可以看出，训练样本越多，各算法的分类精度越高。训练样本的增加，意味着包含的类别信息越丰富，提取的特征能更好地表征不同地物之间的差异性，从而提高分类精度。在相同训练样本数下，SSPCA-LPP的OA和kappa系数均是最高，这是因为SSPCA-LPP兼顾全局和局部信息构造投影矩阵，并在提取局部特征时，对原始数据进行空谱重构，减小像元的信息冗余和噪声干扰，从自信息量的角度引入光谱信息散度，使同类像元之间的权值增大，从而在特征提取的过程中能够保持原有局部结构。

为研究各算法在不同地物上的分类效果，随机选取6%的样本作为训练集，表2是不同算法在不同地物上的分类精度，除“Corn”和“Grass/Pasture-mowed”两类地物，SSPCA-LPP算法在各类地物上的分类精度均是最高，在“Alfalfa”、“Oats”等6类地物上的分类精度达到100%。图2是在6%的样本数下，不同算法在Indian Pines数据集上的分类效果。易知，SSPCA-LPP算法分类后图像的“麻点”明显减少，错分现象比其他算法明显降低。

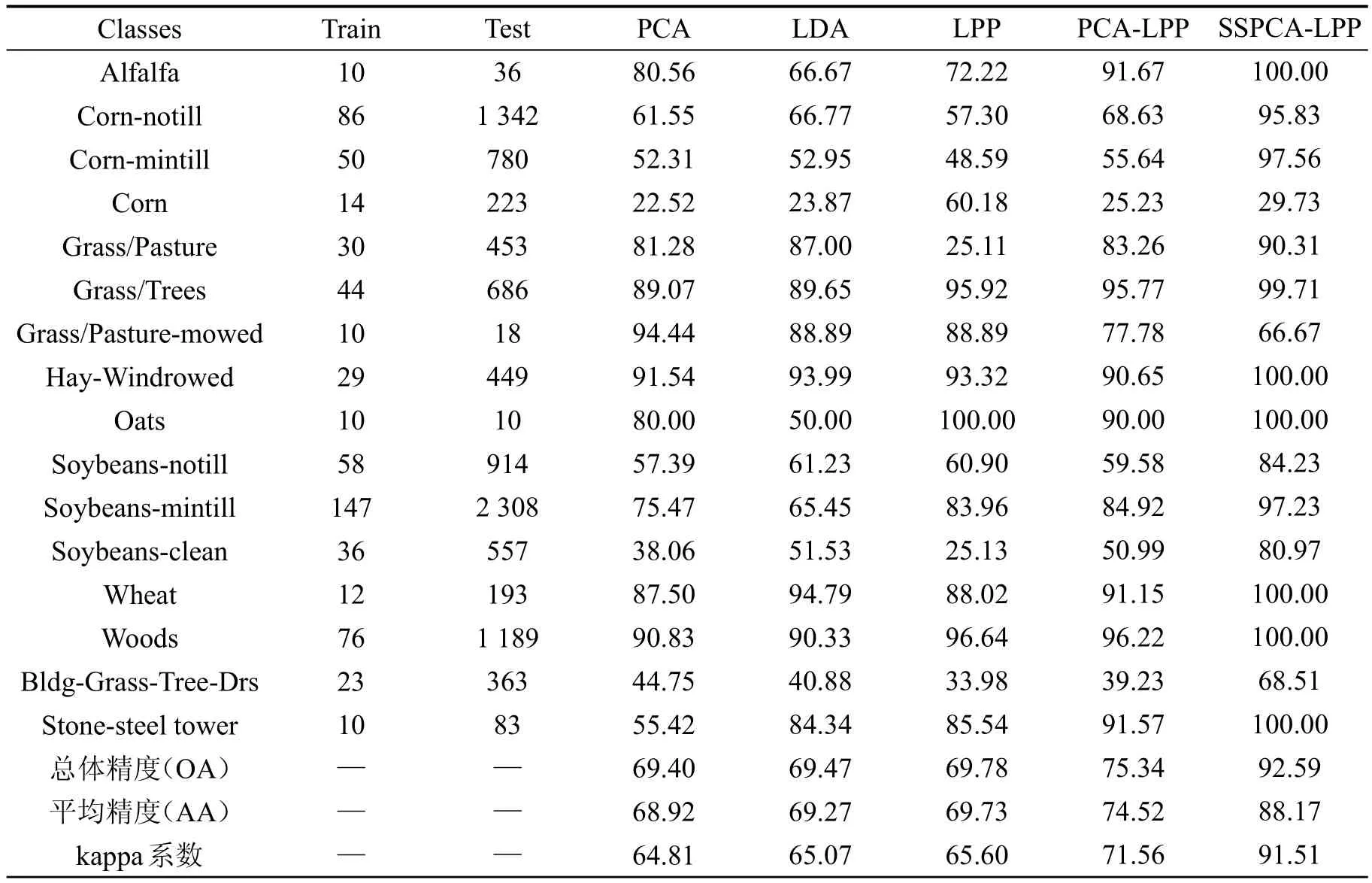
表2 不同算法在Indian Pines数据集上对各类地物的分类结果/%

图2 不同算法在Indian Pines数据集上的分类效果

4 小结

针对高光谱图像分类中易出现“维数灾难”问题，提出了一种空谱联合的PCA-LPP特征提取算法，利用空间一致性原理对高光谱图像进行重构，减小噪声干扰，增强像元的光谱特性，然后对重构后的像元基于空-谱距离度量准则构造局部近邻图，并引入光谱信息散度计算近邻像元的相似性，增大同类像元在近邻图中的权值，使近邻像元在投影之后仍能保持近邻关系，联合PCA、LPP算法构造投影矩阵，在提取全局信息的同时能够保持局部结构。实验结果表明，本文算法的分类效果比传统方法更好。