线性调频信号的检测与调制参数估值*
陶 冶 ,杨喜娟
2
(1.兰州工业学院 电子信息工程学院,甘肃 兰州 730050;2.兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
0 引 言
线性调频(Liner FM)信号是一种脉冲压缩信号,通过非线性相位调制获得了较大的时宽、带宽,时频分析可将一维时间信号映射到二维时频平面,能清楚地揭示信号的时变频谱特性,是对时变、非平稳信号进行分析与处理的强有力工具。目前,对LFM信号常用的时频分析方法是平滑伪Wigner-Ville分布(Smooth Pseudo Wigner-Ville Distribution,SPWVD),这种方法在一定程度上减小了Wigner-Ville分 布[1](Wigner-Ville Distribution,WVD) 二次线性变换产生的交叉项干扰,若对信号的时频分布图进行重排,重排谱图不再满足二次线性,但仍然保持了时移和频移不变性与能量守恒性,减小了交叉项的干扰,增强了时频聚集性,提高了信号分量的定位精度。
1 基于重排的时频分析方法
1.1 LFM信号检测与调制方法
利用时频分析对LFM信号进行检测与调制参数的估计,在重排的SPWVD时频分布图基础上,通过两种不同的方法:常用于图像直线检测的Hough变换方法和利用形态学细化的图像处理方法,完成对LFM信号的检测与调制参数的提取。图1给出了整个流程,两种方法都能准确的判断信号的分量个数;利用Hough变换的直线检测方法相比于形态学细化重排谱图的处理方法抗噪声性能更强,能更好地估计调频斜率,但后者能更好地估计信号的起始频率。
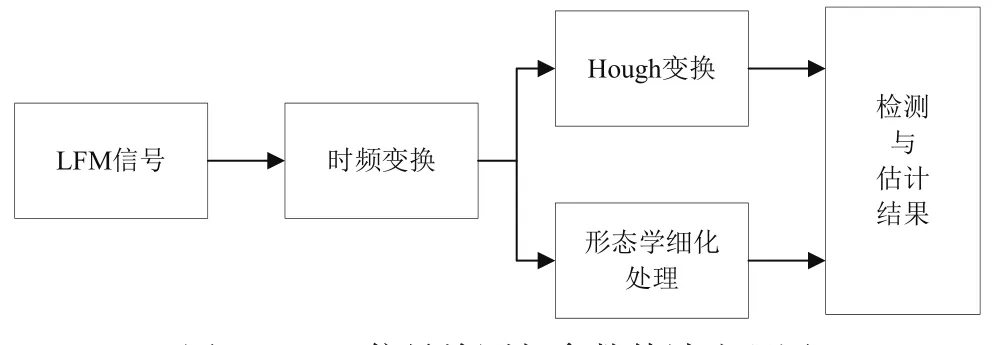
图1 LFM信号检测与参数估计流程图
1.2 LFM信号模型
LFM信号x(t)的复数模型表示为:

其中,A(t)是信号的包络函数,f0是信号的起始频率,k=B/T是调频斜率,B是调频带宽,T是脉冲宽度[2]。LFM信号x(t)的瞬时频率在一个脉冲宽度内是随时间呈线性变化的,其表达式为:

1.3 重排平滑伪Wigner-Ville分布(Reassign Smooth Pseudo Wigner-Ville distribution,RSPWVD)
Wigner-Ville分布(WVD)最初是由Wigner在量子力学提出的,它是一种典型的双线性时频分析方法,其分布结果有着非常直观的物理意义,后来由Ville应用在信号分析领域。
Cohen类时频分布与Wigner-Ville分布存在如式(3)关系[3]:

其中,核函数Φ(s,u)是时频面内的二维低通滤波器,当核函数Φ(s,u)=g(s)h(u)时,即为平滑伪Wigner-Ville分布(SPWVD)。
谱图的重排就是将时频谱图上的任意点(t,f)处计算得到的谱图值转换移动到另外一点(t^,f^),而该点就是点(t,f)附近信号能量的重心[4]。Cohen类时频分布重排后的谱图在任意点(t´,f´)处的值就是所有重排到这一点谱图值的和,定义为:
RCx(t´,f´)=∫Cx(t,f)δ(t´-t^)δ(f´-f^)dtdf(4)
对于Cohen类时频分布中的SPWVD时频分布图[5],时频重排坐标为:

重排后的SPWVD时频分布图表达式为:
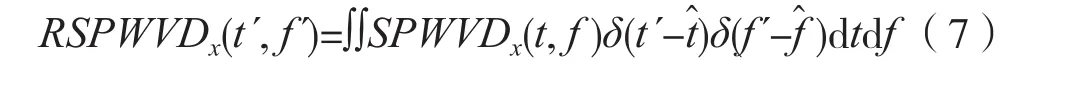
2 LFM信号的检测与调制参数估计
2.1 Hough变换直线检测与估计
Hough变换[6]直线检测就是映射解析直线到参数坐标空间中。Hough变换的标准化参数方程:

Hough变换原理如图2所示,参数空间点(ρ,θ)是由像素点(t,f)经Hough变换映射得到。ρ是图像坐标原点到直线的垂距,θ是ρ与t轴的夹角。

图2 Hough变换原理图
Hough变换就是在图像内沿直线积分,积分值赋给点(ρ,θ),而ρ、θ对应于该直线参数。直线参数上有一个尖峰值,(ρ0,θ0)是尖峰值点在平面上的投影坐标。根据Hough变换可以推导出直线在时频面上的位置,其中起始频率f0和调频斜率k分别为:

对于多分量LFM信号,只需在参数空间(ρ,θ)内预设一定的阈值,找出所有峰值即可求得信号的分量个数和各分量的调制斜率和起始频率。
2.2 形态学图像处理方法
2.2.1 图像的预处理
本文将LFM信号的能量分布图RSPWVDx(t,f)转换为灰度图像Gx(t,f),时频灰度图Gx(t,f)的像素点代表时频分布面上的时频点,灰度图Gx(t,f)的灰度值对应能量幅值。LFM信号在高斯白噪声环境下,灰度图的低频成分代表信号的自分量,灰度图的高频成分代表信号的加性噪声。将灰度图像Gx(t,f)经过低通滤波即去除噪声成分后,再用灰度图像减去估测图像,就可以达到消除图像背景的目的。其算法的流程图[7]如图3所示。
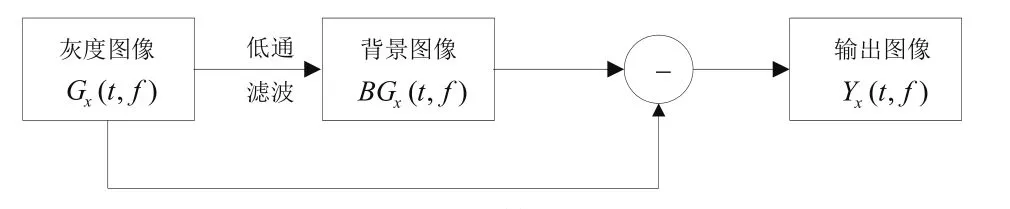
图3 消噪算法流程图
2.2.2 二值图像处理
图像Yx(t,f)初步地抑制了噪声,当SNR较低时仍然会残留部分噪声。在灰度图像Yx(t,f)中的时频点,灰度值低于阈值TH时记为“0”,灰度值高于阈值TH时记为“1”,阈值选取应该尽量保留信号自分量的像素点。这样就得到了二值黑白图像Bx(t,f)。
2.2.3 形态学细化处理
形态学处理[8]就是运用结构元素对集合进行腐蚀和膨胀等操作。细化就是从原始图像中减去利用结构元素对对图像的击中击不中变换。利用结构元素对B对图像A作细化处理表示为:

对图像A多次细化,直到把图像A细化为单像素宽的线条,这样信号在时频图上的自分量就被提取为单像素的线条,提高了时频分布的分辨率。
在得到的高分辨率时频图中,行和列分别对应着时间和频率,对图像进行扫描,可以找到信号起始频率f0的位置。信号的调频斜率k也可由细化后的直线求得。
3 仿真实验及结果分析
为了有效地比较各方法,我们用MATLAB7.6中的时频工具箱[9]对LFM两分量信号进行仿真实验。仿真中本文选择SNR分别是0 dB、3 dB和无噪声的上述LFM信号,用本文提到的方法进行实验,提取信号的起始频率及调频斜率。

图4 实验信号的时域波形
图4(a)表示两分量中一个分量LFM信号的调频宽度为6 MHz,另一个分量LFM信号(见图4(b))的调频宽度为7 MHz(见图4(c)),起始频率为14 MHz,给出两分量LFM信号的检测与估计所有实验结果。

图5 两分量LFM信号的SPWVD时频分布图、RSPWVD时频分布图、Hough检测结果、形态学细化处理结果,无噪声
图5信号为两分量信号,其中图5(a)、图5(b)图参数为Lg=50,Lh=125,NF=1 000,Threshold=5%。表1和表2给出了不同SNR下,利用Hough变换直线检测和形态学细化两种方法处理后,对LFM信号调制参数估计值。从表1和表2中可以看出,两种方法均能有效地对信号的分量个数作出判断,较好地估计LFM信号的调制参数。Hough变换的直线检测方法较形态学细化算法更不易受噪声干扰,调频斜率估计较好。
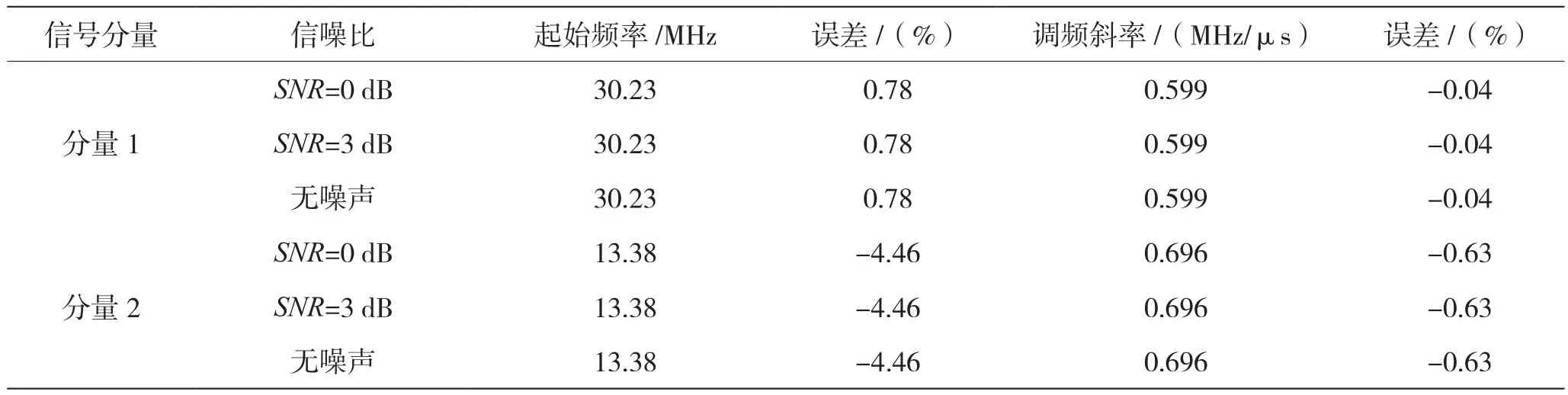
表1 两分量LFM信号的Hough变换直线检测与估计实验结果

表2 两分量LFM信号的形态学处理实验结果
4 结 语
系统利用基于重排谱图的Hough变换直线检测和形态学细化图像处理两种不同方法进行信号检测与调制参数估计。实验结果表明,重排时频谱图增强了时频聚集性,减小了交叉项的干扰;两种方法均能有效判断信号分量的参数;二者相比,前者能更好地抑制噪声的干扰,调频斜率估计误差更小;后者估计的信号起始频率更准确。在实际应用中,可根据需要选择合适的方法对信号进行检测或将二结合起来共同解决问题。

