基于云模型与Fibonacci的混沌伪随机序列发生器设计

魏连锁， 胡现成， 郭 媛， 陈 炜， 马志昇

(齐齐哈尔大学 计算机与控制工程学院， 黑龙江 齐齐哈尔 161006)

0 引 言

混沌是一种非周期的动力学过程，具有不确定性、不可重复、不可预测的特性，它看似杂乱无章，其实混沌中蕴涵着有序[1]，这是其非线性动力系统的固有特性。伪随机序列广泛应用于密码、调频以及调频通信系统中,并且混沌系统产生的信号很难被破解。混沌的应用是需要混沌伪随机序列发生器来产生混沌序列，并且生成速度快，被广泛使用，而随着现在混沌解密对象的复杂性与安全性要求的提高，对混沌序列的要求也越来越高。

对混沌系统或混沌伪随机序列的要求是随机性好、安全性高、均匀分布、长期不可预测等，但是对于一般混沌会存在不连续、可控参数少等问题。文献[2]中就提到了一维Logistic映射，但在计算过程中出现周期退化、复杂度低和映射函数容易被破解等问题。文献[3]中提出的组合设计新一维混沌系统来提高区间大小以及不连续等性能，但周期退化以及周期有限问题没有解决。另外，在文献[4]中提出的多混沌联合可以发现，通过合适的级联组合方式能够提高伪随机性。文献[5]中提出一种基于混沌和Fibonacci伪随机数列(F-L)的加密方法，提高了混沌序列的随机特性，改进了有限周期性的局限性。Zhou等[6]提出将两个一维映射并联后进行模1相加的改进方法得到了性能较好的新一维混沌映射。文献[7]中利用Logistic混沌映射来产生Arnold映射控制参数，再利用Henon混沌生成序列，该算法产生的混沌安全性更高。文献[8]中提出将3个不同的二维混沌映射结合生成混沌序列，具有高维的随机性和复杂度高等优点。因此，将多混沌进行结合可以很好的提高混沌的随机性。

Fibonacci序列产生速度快以及可控参数多等优势很适合在随机序列发生器里应用，但是存在随机数不居中及序列的显著相关性现象[9]，为了克服存在问题，将在云模型里云的数字特征下产生的若干云滴作为三阶Fibonacci函数的数值来源，结合云模型的随机性以及数据的居中分布特性，来提升混沌的随机特性。现在基于云模型的云技术已被成功地应用于计算机多领域。云模型是反映了客观世界中概念的两种不确定性，即随机性和模糊性。

本文介绍了基于云模型Fibonacci混沌系统(Cloud-based Fibonacci Chaotic System，CFCS)，以云模型作为数值来源，利用量子Logistic(Quantum Logistic，QL)混沌序列作为三阶Fibonacci函数模型参数，Logistic 映射来级联耦合，采用多混沌与多发生器的结合来产生了满足实际应用的随机序列。最后从密钥空间、初值敏感性、相关性、互信息、差值特性、分布特性、复杂度、相空间结构等多方面具体分析发现混沌序列具有随机性且安全可靠。

1 混沌伪随机序列发生器设计

混沌伪随机序列是由数学公式计算产生，从数学层面上讲，想实现理想的应用，伪随机序列的周期需要足够大，并且符合各项检验要求。该发生器采用 Fibonacci数列“扰动”的方法来得到混沌序列，实现多参数控制，不仅提高复杂度，而且弥补了Logistic混沌序列分布不均匀的缺点；同时，云滴的产生是随机的，且始终存在着细微的变化，将云滴与Fibonacci系统结合，实现混沌序列的不重复性。

1.1 云模型

云模型是用语言值表示的某个定性概念与其定量表示之间的不确定性转换模型，云模型具有期望值Ex、熵En和超熵He3个数字特征[9-10]。

Ex反映了在云滴群里云重心的位置，

(1)

样本方差：

(2)

En揭示了模糊性和随机性的关联性，

(3)

He是对En的不确定度量，反映了云的离散程度和厚度，

(4)

生成以En为期望值，He2为方差的一个正态随机数，

yi=RN(En,He)

(5)

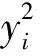
xi=RN(Ex,yi)

(6)

由云模型数字特性产生的云滴分布如图1(a)所示，具有正态分布特性，其中xi居中分布，如图1(b)所示。云发生器的数据虽然不像混沌具有分布均匀特性，但是云模型的随机性应用到混沌发生器上，解决了混沌序列长期不可预测性的问题，每一次混沌发生器的运行会随机产生一组混沌随机序列，序列的规律将

(a) 云滴图

很难被发现。随着随机因子的随机变化，每次的随机序列无法找到周期规律，特别是在加密应用中会起到很好的加密效果。

1.2 云模型Fibonacci混沌系统模型

由Fibonacci 数列产生随机数，序列本身存在显著的相关性，所以需要对它进行改进，这样才能满足实际的需要，对经典的Fibonacci 数列进行改进得到延迟的Fibonacci数列[11-12]：

xi+1=(xi+xi-p)modM

i=p,p+1,…,M∈N

(7)

Fibonacci数列具有简单、快速、易于实现等特性，因为Fibonacci 数列本身具有自相似性，因此采用广义三阶Fibonacci函数模型：

Fj=(AiFi-1+BiFi-2+CiFi-3)modM

(8)

量子Logistic映射的表达式为:

(9)

式中：Ai、Bi和Ci表示随机常数；M为模；Ai,Bi,Ci为选取QL混沌映射所产生的变量xi、yi、zi序列组合，其初值x0= 0.3，y0=0.06，z0=0.2，r=3.99，β=6.2；Fi为取值Ex=5 000，En=3，He=0.1的云滴群，再通过取模运算产生Fj序列。

采用QL混沌映射作为随机变参数来增加序列的随机性，降低相关性。经过广义三阶Fibonacci的函数模型处理后，再与 Logistic映射耦合得到广义三阶Fibonacci混沌系统：

(10)

式中：Q(γ,β)表示QL混沌系统；F(Q(γ,β))表示将云滴代入到式(8)广义三阶Fibonacci函数模型的序列Fj；L(x0,μ)表示初始状态为x0以及参数为r的Logistic混沌系统。最后通过与Logistic映射耦合产生新的均匀且非相关的混沌序列。图2所示为CFCS伪随机序列发生器的设计示意图。

1.3 伪随机发生器设计步骤

步骤1选取量子Logistic混沌系统的初始值及系统控制参数，代入QL混沌系统中，得到xi、yi和zi均在(0,1)范围内的实数三阶序列(xi，yi，zi)。

步骤2选取云模型期望值Ex、En、He3个参数的初始值，利用云发生器生成随机的云滴群。

步骤3将步骤1产生的QL混沌三阶序列(xi，yi，zi)代入式(8)中分别作为广义三阶Fibonacci函数模型的参数Ai、Bi、Ci，并将步骤2中的云滴代入式(8)

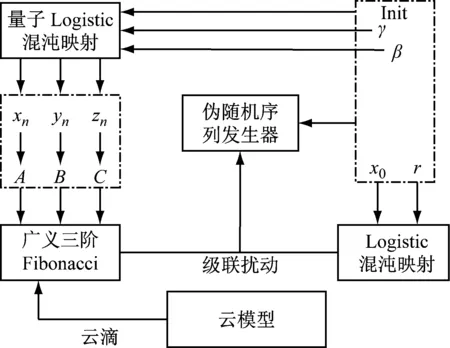
图2 CFCS伪随机混沌序列发生器示意图

中作为广义三阶Fibonacci函数模型的函数值Fi，产生广义三阶Fibonacci函数模型序列。

步骤4步骤3中通过式(8)产生的广义三阶Fibonacci函数模型序列与Logistic混沌系统代入式(10)中级联耦合，广义三阶Fibonacci混沌系统产生最后所需的均匀非相关的序列。

根据上述步骤设计的伪随机序列发生器相比于一般的序列发生器具有较好的伪随机特性，生成速度快、序列独立不重复且具有较高的安全性，产生均匀且非相关的伪随机混沌序列如图3所示。

图3 伪随机序列值分布图

2 混沌伪随机序列分析

2.1 密钥空间分析

密钥空间分析是一个重要的检测方法，它是对随机序列发生器在产生加密密钥应用的可行性的必要检测。检测选取混沌系统的初始值和控制参数作为密钥，检测目标需要密钥空间足够大才能保证安全性。实验数据表明，将该算法的数据精确到小数点后11 位，密钥空间为1011×6= 1066≈2219，远大于2128的密钥空间，增大了抵抗密钥攻击的能力[13]。

2.2 初值敏感性分析

初值敏感性分析是安全性说明的重要部分，伪随机序列拥有好的初值敏感性才能满足实际应用。通过对密钥初始值进行轻微的改变，观察产生的序列与原始序列是否有强烈的变化。利用CFCS产生两个混沌序列，其中1个为原始序列；另1个则是对初始值取偏差为10-11所得到的新序列，图4为两序列的差值图，区间变化的差值说明该算法对密钥初始值具有很强的敏感性。

图4 两序列差异图

2.3 相关性分析

相关性分析[14]是混沌序列随机性分析的关键步骤，好的相关性是系统能够可靠运行的重要保证之一。自相关函数是描述在任意两个不同时刻分别取初值x0=121，x0=121+10-11的相关程度；互相关函数给出了两个随机序列是否相关的一个判断指标，自相关描述同一序列在不同的时刻的相关程度。

在QL混沌系统初始参数取x0=121，x1=2.0，x2=2.0,M=191，CFCS产生的序列具有自相关和互相关特性，通常认为相关系数在0～±0.09为没有相关性，0.1～±0.30为弱相关，如图5所示。由图5可见序列具有类似δ-like的性质，有尖锐的自相关特性和良好的互相关特性。

(a) 序列的自相关特性

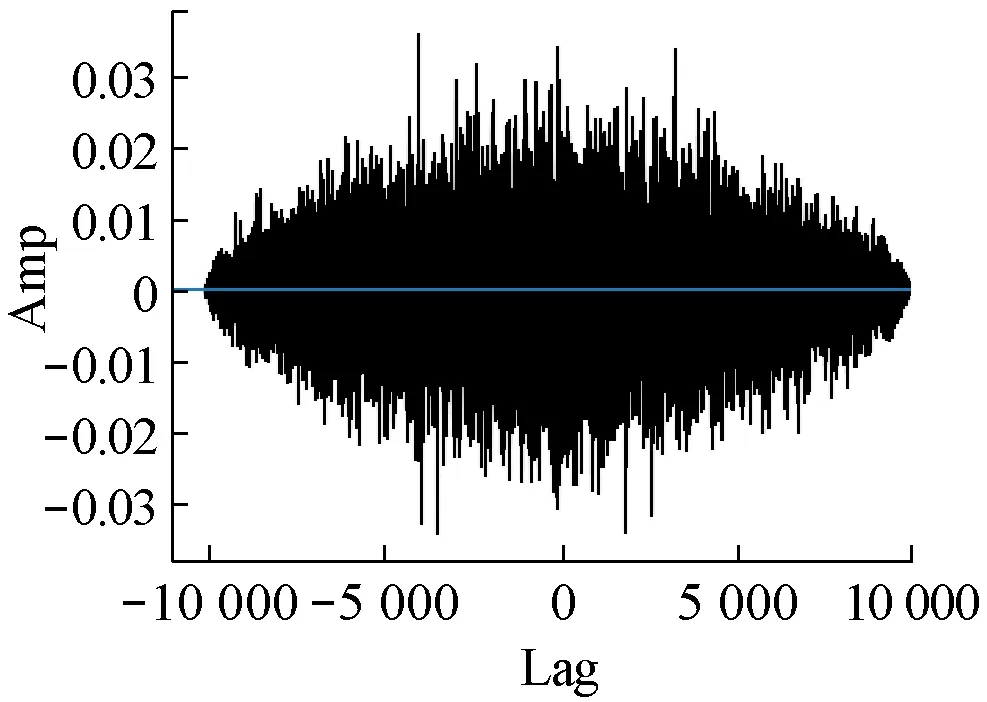
(b) 序列的互相关特性

图5 序列相关性分析图

2.4 随机性测试

随机性采用美国 NIST公布的 SP 800-22 随机数测试标准对序列进行测试，即SP800-22 标准[15]。该标准从不同角度检验伪随机序列在统计特性上相对于理想随机序列的偏离程度，通过该检验标准可以判断出伪随机序列的随机性能[16]。

计算判断标准P-Value 的计算公式:

式中：erfc为互补误差函数；sabs为统计值。评判标准为若P-Value>0.01，认为测试的序列符合随机序列; 反之，则认为序列不满足随机序列的要求。由上述测试方法得P-Value = 0.852 18> 0.01，故可认为序列是随机序列；任意取7次的测试数据分别为：0.723 97，0.898 65，0.710 72， 0.708 45，0.719 65， 0.526 68，0.392 39。由于云模型云滴的模糊性与随机性，随着随机因子的变化，产生不重复的混沌序列，取N(N>100)次测试P-Value 的值均大于0.01。

3 混沌伪随机序列的对比分析

为了更直观展现CFCS伪随机序列的特性，分别对QL(x轴)、F-L混沌和CFCS进行对比，选取了典型的序列直方图、序列复杂度等测试方法进行对比分析。

3.1 序列直方图

为了更直观地观察系统输出序列分布均匀情况，绘制了图6所示的直方图。

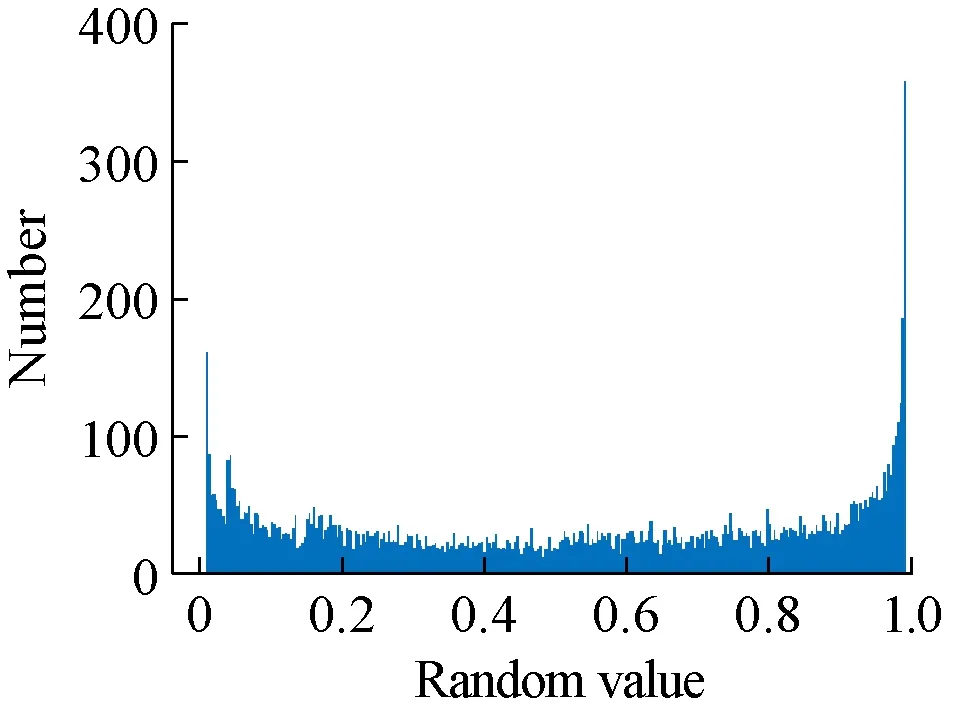
(a) QL直方图

(c) CFCS直方图

由图6可以看出，QL、F-L系统和CFCS生成的混沌序列的分布特点，图6(a)QL(x轴)直方图,(b)F-L直方图分布不均匀，并且初始值对QL影响很大，而CFCS采用 Fibonacci数列“扰动”的方法来得到混沌序列，并且将云模型云滴群作为广义三阶Fibonacci函数模型函数值，使得混沌序列随机性及复杂度提高，混沌序列分布更加均匀平滑，没有出现波动较大的现象，符合随机序列发生器的要求。

3.2 序列复杂度

序列复杂度表示了序列与理想随机序列的相似程度，通过序列复杂度的大小可以判断序列的复杂情况，其数值越大，说明与理想随机序列越相似，就越难以被恢复，安全性越高[17]。Pincus等提出的近似熵(ApEn)方法，可以很便捷地计算出序列的复杂度[18]。图7中给出了F-L系统、QL和CFCS的ApEn值，对比复杂度曲线可以得到以下结论：CFCS模型生成的伪随机序列的ApEn值最大，约为1；其他几种模型数值偏低 。这充分说明此模型生成的伪随机序列的复杂度明显高于F-L系统、QL模型产生的伪随机序列。

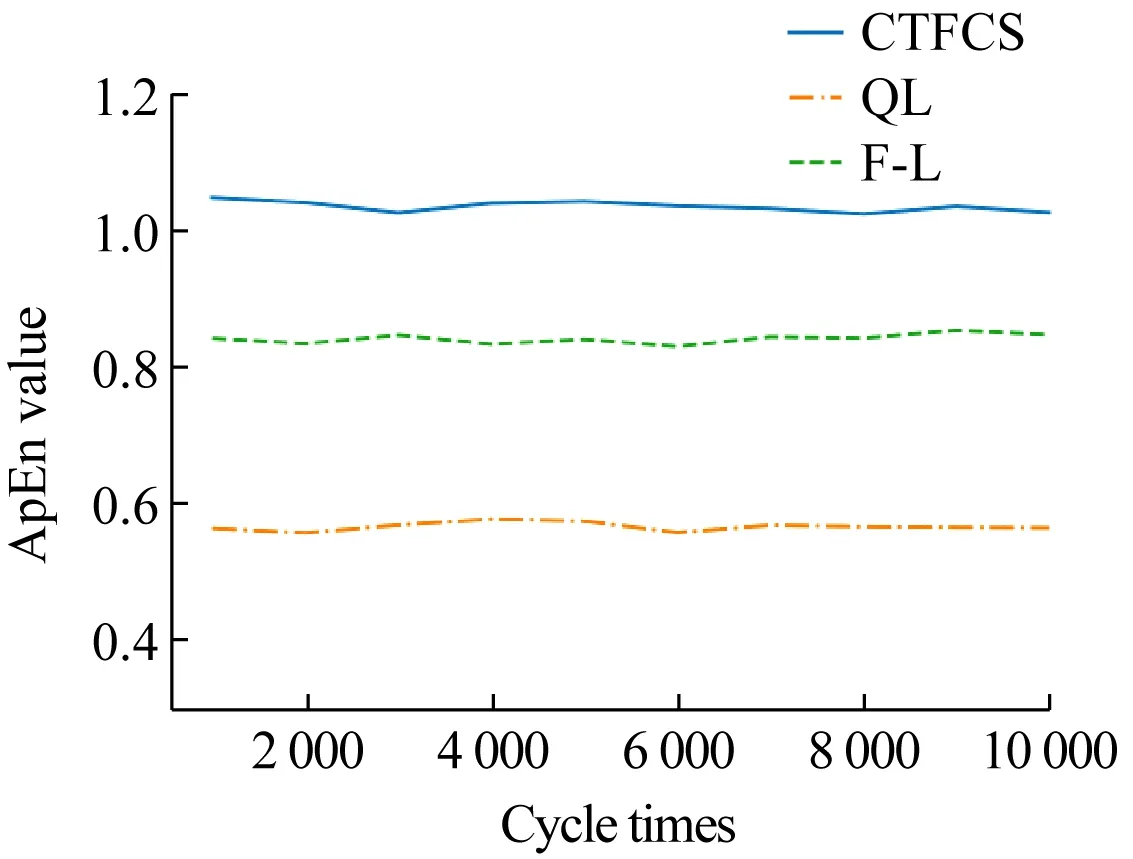
图7 近似熵

3.3 空间分布

对3个模型伪随机序列的连续数值构造空间结构图，以QL(x轴)、F-L系统、CFCS生成的序列xn为基础进行取点，以点(xi，xi+1)绘制二维空间结构图，遍历完整个序列xn得到图8(a)QL(x轴)空间二维结构图、图8(b)F-L空间二维结构图和图8(c)CFCS序列空间二维结构图。

(a) QL(x轴)空间二维结构图

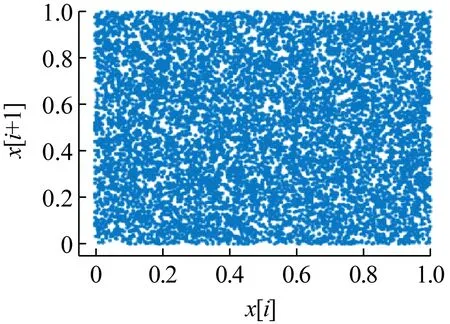
(c) CFCS空间二维结构图

由图8可以看出，QL混沌映射输出序列空间结构呈现曲线特征，说明具有较高的相关性，而F-L存在分布不均匀的现象，并且是随着迭代的次数增加，随机数的分布呈现出初始过于密集，逐渐出现稀疏不均匀分布的现象，而图8(c)CFCS序列以量子Logistic混沌序列作参数、云模型随机云滴群做输入与Logistic 映射级联耦合，不仅增加了可控参数的数量，同时利用混沌序列再次作为数据的输入，增强了数据混沌性，使得序列分布表现出了好的均匀性和无序性。

4 结 语

本文设计了一种伪随机序列的生成算法，该生成器能产生伪随机性强、分布均匀、相关性小的伪随机序列。通过对随机序列的密钥空间、初值敏感性、相关性的分析，证明该方法具有很好的随机性且安全可靠。除此之外，还通过与其他序列的信息熵、序列直方图、序列复杂度进行对比分析，序列表现出良好的伪随机序列，具有结构简单、伪随机性强、分布均匀、相关性小等特征，该发生器具有很好的应用前景。