基于模态分析的扣件弹条扣压力测试方法

王绍华，韦 凯

(西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031)

扣件系统作为铁路轨道结构的重要部件，用于保证钢轨与支承体之间的可靠联结。其中，扣件弹条主要提供扣压力，将钢轨固定在铁垫板上，防止钢轨纵向爬行和翻转。然而，在轮轨系统的长期作用下，扣件系统易出现疲劳、松动甚至失效现象。这类扣压力不足的问题在能用可视化方法评价之前，弹条扣压力早已不能达到正常工作的标准，这将为轨道系统的稳定及安全行车带来极大的隐患[1]。及时发现松动或失效的扣件，保证扣件系统的足够扣压力是铁路工务维护部门的一项重要工作[2-3]。

目前，在扣件弹条扣压力测试方面，TB/T 3396.2—2015《高速铁路扣件系统试验方法 第2部分：组装扣压力的测定》[4]中规定了高速铁路扣件组装扣压力的室内测试方法，通过测定使钢轨脱离钢轨支承表面的力来确定扣件组装扣压力。但该方法局限性较大，需要使用特定的加力架装置且工作量大。发明专利[5-6]提出了一种扣件弹条扣压力的测试装备与方法，但此类装备与方法需要在现场精确安装重型加载设备，存在工作强度大、检测效率低等缺点，无法快速普查铁路全线的扣件弹条扣压力。为了适应铁路交通的快速发展，保证行车安全，亟需开发扣件弹条扣压力的快速无损检测方法。目前我国现有的扣件弹条扣压力检测方法主要为直接测试法，鲜有从扣件系统自身振动特性出发对其扣压力采取间接测试方法。

查阅文献发现，Oda等[7]采用理论研究和试验方法，得出了服役状态下扣件弹条扣压力会直接影响包括扣件系统在内的实际轨道的动力学行为。Thompson等[8]通过试验研究得知扣压力对扣件系统高频动态特性影响较大。由于不同服役状态下弹程(扣压力)对弹条非线性动刚度特性的影响，进而导致安装状态下弹条扣压力对其固有频率的影响较大。

基于以上研究，本文利用扣件系统自身振动特性，对弹条扣压力采取间接测试方法。选取我国地铁常用的Ⅲ型弹条弹性分开式扣件系统为研究对象，采用UG建模软件及ANSYS有限元软件建立扣件系统精细化有限元模型；并基于非线性有限元理论(包括材料、几何及接触非线性)与模态分析方法，计算得到不同弹条扣压力(弹程)与弹条固有频率的对应关系，提出一种铁路钢轨扣件弹条扣压力的间接测试方法。该研究可为铁路扣件弹条的检测和维护提供科学依据。

1 扣件系统三维非线性有限元模型

1.1 有限元模型

传统建模方法是将弹条与周围部件接触部位的边界加以约束，并将某一约束点或面代之以外力。这种计算模型不能真实地反映弹条的受力情况，并且可能引起局部应力集中现象，导致计算结果偏差大。在实际分析中发现，未与弹条直接接触的部件同样会影响弹条的受力特性。因此，为了能准确地模拟扣件弹条服役状态，本文考虑了扣件系统关键部件，主要包括钢轨、弹条、铁垫板、轨距挡块、轨下弹性垫板等，各部件均采用原比例尺寸建立实体有限元模型，其中钢轨长度取半跨扣件间距(0.3 m)。通过多次试算及比较网格数量和类型对结果的影响，最后确定模型共划分 75 659 个六面体单元和 78 106 个节点。扣件系统有限元模型如图1所示。

图1 Ⅲ型扣件系统有限元模型

1.2 材料属性

根据GB/T 1222—2016《弹簧钢》[9]，Ⅲ型弹条材料采用60Si2MnA。考虑扣件弹条在工作环境下非线性(弹塑性)变形，其本构模型采用理想双线性强化弹塑性模型，如图2所示。弹条屈服强度为 1 375 MPa，极限强度为 1 570 MPa。轨距挡块材料为玻璃纤维增强聚酰胺66，弹性胶垫材料采用热塑性聚酯弹性体(Thermoplastic polyester elastomer，TPEE)，铁垫板材料采用QT450-10球墨铸铁。材料详细参数见表1。

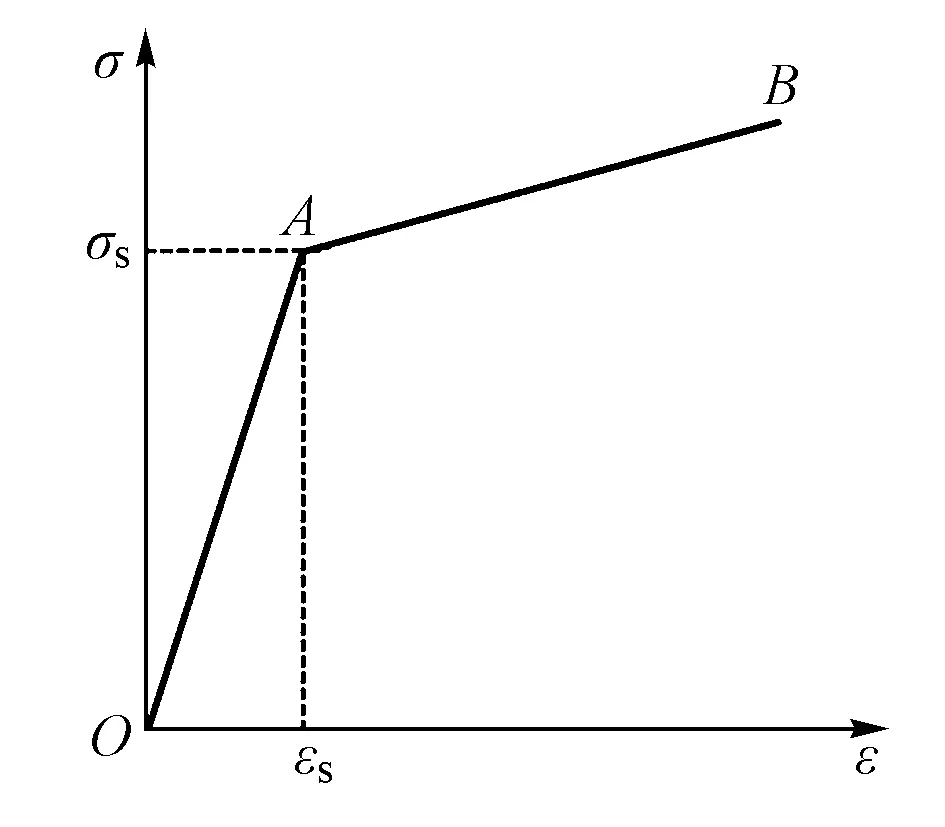
图2 理想双线性强化弹塑性模型

表1 扣件系统各部件材料参数

1.3 接触及边界设置

为了比较真实地模拟弹条工作时的受力状态，本文采用面-面接触单元模拟弹条与铁垫板和轨距挡块的相互作用关系，即采用非线性接触理论来处理弹条边界条件。接触算法采用扩展拉格朗日算法，接触对间的摩擦和运动状态根据库仑摩擦模型确定，扣件系统各部件接触关系设置见表2。

表2 扣件系统各部件接触关系设置

2 预应力状态下的模态分析方法

结构的振动特性决定了结构对于其他各种动力荷载的响应情况，而模态分析可用于分析结构的振动特性。根据弹性力学，建立弹条系统运动方程为

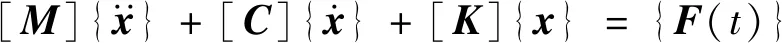
(1)

在不施加外力的情况下，F(t)=0，则此时得到扣件系统的自由振动方程。在研究弹条的固有动力特性时，工程上通常不考虑阻尼的作用及影响，即可得到无阻尼振动方程为

(2)

相应的特征方程为

([K]-ω2[M]){x}={0}

(3)

式中，方程的根ωi为弹条第i阶模态固有频率(i=1,2,…,n)。

在实际工作环境中，由于弹条弹程(扣压力)的影响，产生预应力效应，则考虑预应力的弹条振动方程为

(4)

式中，[KD]为预应力状态下弹条附加应力刚度矩阵。

在有限元求解过程中，将弹条进行实体单元划分处理，其中任一单元的附加应力刚度矩阵[Kd]表示为

(5)

其中

(6)

(7)

(8)

式中：Ni(i=1,2,…,n)为形函数；[Km]为扣压状态下相应单元的预应力矩阵，与不同弹程(扣压力)相对应。

通过将有限个单元的附加应力刚度矩阵[Kd]组合，得到预应力下整个弹条的附加应力刚度矩阵[KD]。

3 基于模态分析的扣件弹条扣压力研究

3.1 模型验证

为了验证扣件弹条有限元模型的正确性，本节计算自由状态下 2 000 Hz 范围内扣件弹条各阶模态，结果见图3，图中阴影部分表示变形前的状态，并将计算结果与既有文献进行对比分析，对比结果及各阶模态振型描述见表3。

图3 扣件弹条自由状态下模态

由表3可知，本节计算结果与文献[10]中理论分析与试验测试结果相差较小，因而可验证本文扣件弹条有限元模型的可靠性。

3.2 扣件弹条静力计算分析

本文通过抬升铁垫板中间部分，使弹条达到正常安装。在铁垫板中间部分进行抬升前，先将铁垫板两侧部分设置全约束，然后对铁垫板中间部分向上施加位移荷载，使铁垫板中间部分同两侧部分在同一个水平面内。

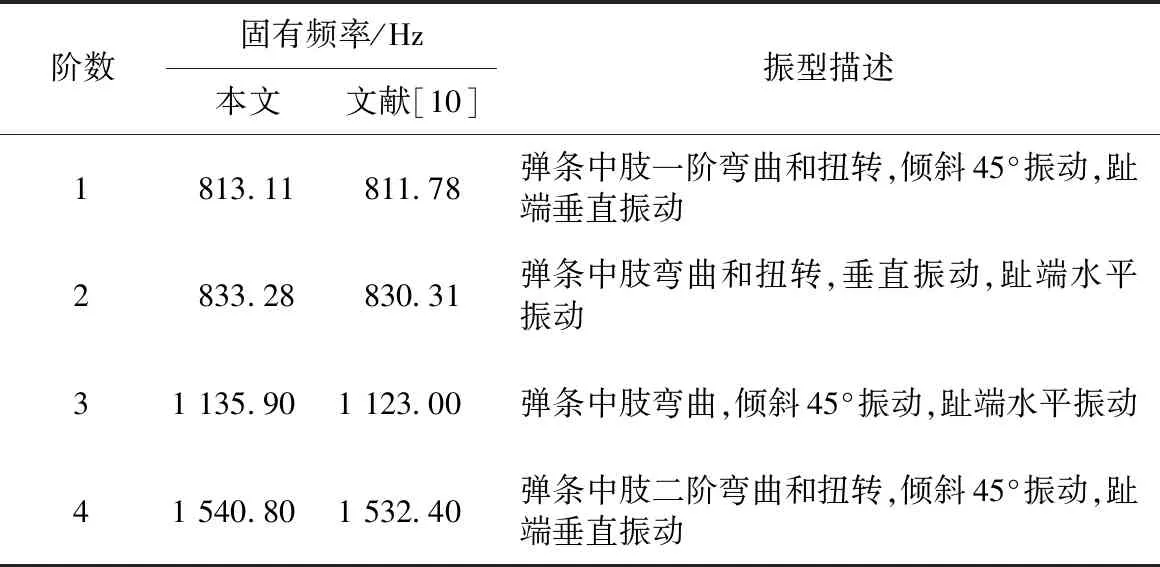
表3 扣件弹条自由状态下模态振型

然后对扣件系统进行静力分析，即以铁垫板中间部分垂直向上施加的位移荷载对弹条施加弹程，以达到弹条扣压状态。以铁垫板中间部分抬升14 mm为例，此时弹条弹程为13.0 mm，弹条扣压力为11.8 kN，弹条最大等效应力为 1 478.2 MPa。弹条应力与位移云图如图4所示。

图4 扣压力11.8 kN时弹条的应力及位移云图

3.2.1 弹程对扣压力的影响

当铁垫板中间部分垂直抬升不同高度时，弹条弹程与扣压力关系曲线见图5。

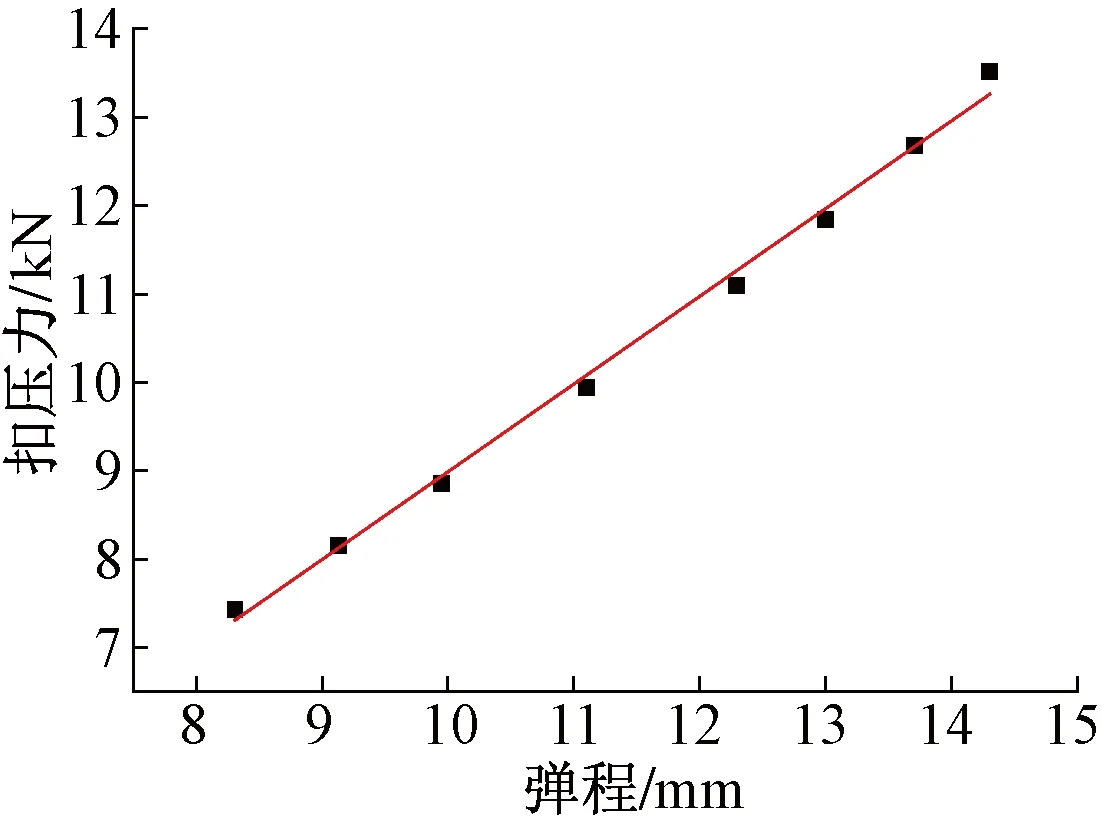
图5 弹条弹程与扣压力关系曲线

通过对计算结果分析可得到弹条扣压力与弹程之间的拟合公式为

P=1.01H-0.95

(9)

式中：P为弹条扣压力，kN；H为弹条弹程，mm。

弹条扣压力与弹程基本呈线性关系，即弹条刚度约为1.0 kN/mm。

3.2.2 轨下胶垫刚度对扣压力的影响

当轨下胶垫刚度分别为30，40，50 kN/mm时，弹条弹程与扣压力的关系见图6。可知改变轨下胶垫刚度主要影响弹条弹程的变化，进而影响其扣压力。即正常扣压状态下弹条扣压力与弹程始终呈近似线性关系，该对应关系不随轨下胶垫刚度变化而改变。

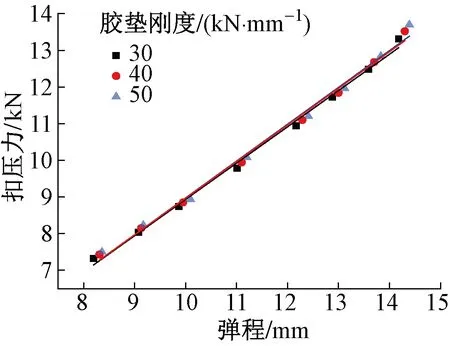
图6 轨下胶垫刚度对弹条扣压力的影响

3.3 预应力状态下的模态分析

通过对弹条无约束状态下的频域分析，已经得到了弹条的固有频率、振型以及敏感频率。然而，扣件系统在正常服役状态下弹条已经发生变形从而产生了扣压力，属于带有预应力的系统。为了进一步计算弹条在服役状态下的敏感频率及振型，有必要研究弹条在正常服役状态下的振动特性。

在上节扣件系统模型静力计算分析的基础上，充分考虑扣件弹条在弹程作用下几何非线性问题(即大位移小应变状态)，对其进行模态分析，得到不同预压力下弹条的各阶固有频率及模态振型，继而建立弹条扣压力与固有频率之间的联系。

在上节静力分析的基础上，对其进行服役状态下的模态分析，可得到当弹程为13.0 mm时(扣压力为11.8 kN时)弹条在1～2 000 Hz 内的固有频率，见图7，对应振型见表4。

图7 服役状态下扣件弹条固有频率

表4 服役状态下扣件弹条模态振型

根据设计要求，Ⅲ型弹条扣压力的正常服役范围是不小于11 kN，且不大于考虑最大残余变形的安全扣压力[11]。通过对扣件弹条预应力下模态分析发现，不同扣压条件下弹条第1阶固有频率与扣压力之间大致呈线性关系，拟合公式为

P=0.016f-1.79

(10)

式中，f表示组装扣件弹条工作频率(即第1阶固有频率)，Hz。

图8为弹条固有频率与扣压力关系曲线。可知，Ⅲ型弹条在有效扣压范围内弹条的工作频率(第1阶固有频率)为800～1 040 Hz，而在有效扣压范围内弹条第2阶固有频率为 1 600～1 840 Hz。

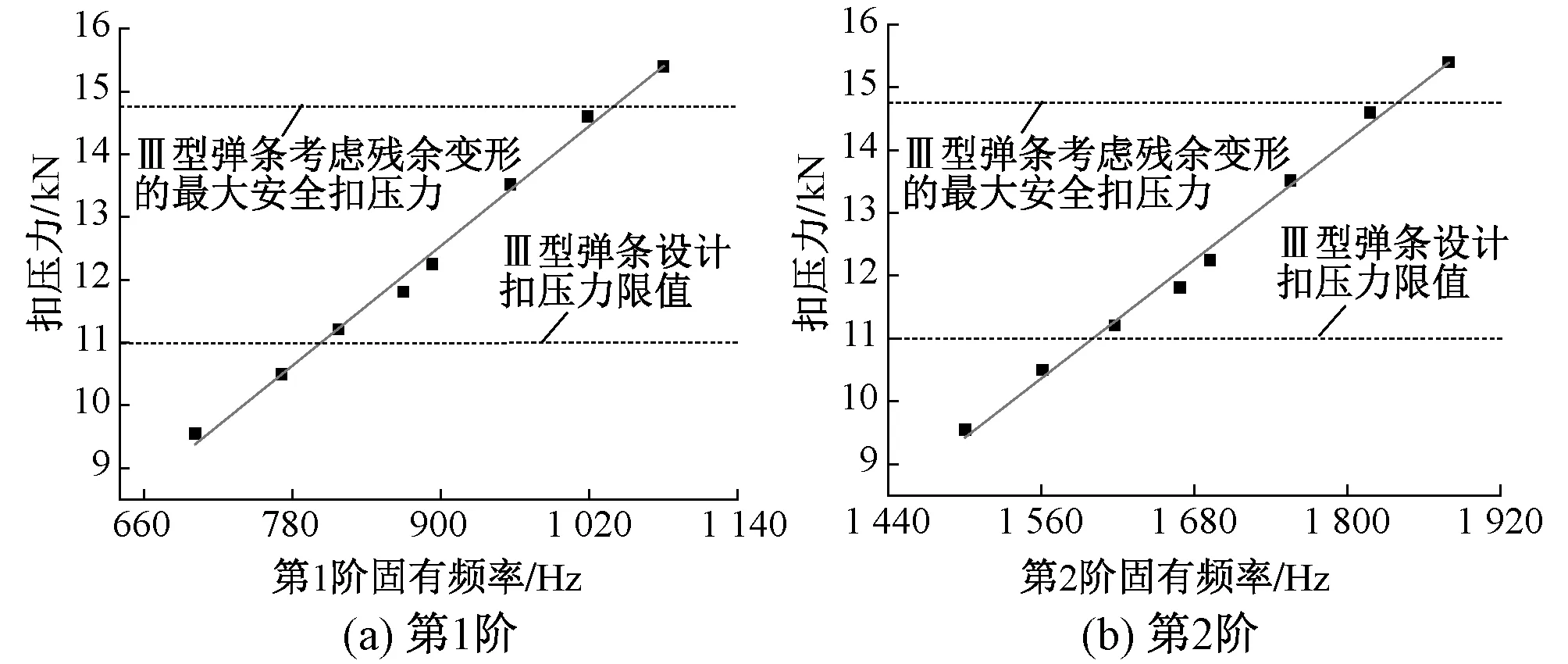
图8 弹条固有频率与扣压力关系曲线

3.4 弹条扣压力间接测试方法

从上节对服役状态下的扣件弹条模态分析可知，Ⅲ型弹条第1阶模态振型主要为弹条前拱大圆弧垂向振动，因此将加速度传感器布置在弹条前拱大圆弧处，并对弹条趾端进行力锤敲击，然后采集振动响应信号。通过对力信号与加速度信号进行加窗处理后，可快速获得拾振点的加速度频响值，进而得到对应的弹条第1阶工作模态频率，然后依据弹条扣压力与弹条第1阶固有频率的对应关系，可间接得到扣件弹条服役状态下的扣压力(弹程)。

4 结论与建议

1)扣件弹条扣压力与弹程基本呈线性关系，其对应关系与轨下胶垫刚度无关，且Ⅲ型弹条扣压力同弹程的变化关系约为1.0 kN/mm。

2)扣件弹条扣压力(弹程)与其固有频率近似呈线性关系，根据Ⅲ型弹条正常服役状态设计要求以及考虑最大残余变形的安全扣压力，可得Ⅲ型扣件弹条在有效扣压范围内的工作频率(第1阶固有频率)为800～1 040 Hz。

3)扣件系统弹条固有频率主要受扣压力(弹程)影响较大，通过有限元分析得到不同扣压状态下弹条扣压力与其固有频率之间的关系，提出一种适用于铁路扣件弹条扣压力的间接测试方法。该方法易于工程运用，可用于快速评价铁路各类扣件系统的弹条扣压力，为铁路扣件弹条的检测和维护提供科学依据。

4)由于本文测试方法仅从理论角度解释了利用扣件系统自身振动特性实现对其扣压力的间接测试，后续研究将结合现场大量扣件弹条扣压力的测试数据，进一步验证本文测试方法的可靠性。