倒Y型四能级原子系统的侧向位移*

陈芳芳

（杭州电子科技大学通信工程学院，浙江 杭州 310018）

0 引 言

在 1943年，Goos和 Hänchen[1-2]在研究光传输到折射率更大的介质中发生全反射时，发现并用实验定量的测量了反射光线的古斯-汉欣（Goos-Hänchen，GH）位移，即反射光的侧向位移，打破了人们对全反射的错误认识。之后，Artmann[3]和Renard[4]等人分别提出根据反射、入射光之间的相位差表达式和能流守恒定理能解释和计算该位移。反射和透射光的侧向位移在微纳光学、光波导开关、量子和等离子体物理学等中具有潜在的应用前景，因此从发现至今受到了人们广泛的研究[5-7]。目前已经有很多对不同热门材料的GH位移的研究，比如：拓扑绝缘体、手征特异材料和左手材料[8-10]，分别可以通过拓扑磁电极化率、手征参数和左手材料的材料参数控制其表面的侧向位移大小。近几年，通过量子相干和干涉效应研究了掺杂了原子的固定结构[11-13]中透射和反射光的侧向位移特性，可以实现在不改变材料结构的同时方便地调控位移，为未来在光和量子通信中的应用奠定了基础[14-15]。

量子非线性光学中的量子相干能导致很多独特的现象，比如电磁诱导透明、电磁诱导吸收以及非线性Kerr效应等[16]。Wang等人[13]首次通过控制耦合场的强度研究了量子相干效应对掺杂有两能级原子系统的固体结构中光束侧向位移的作用。之后，Ziauddin[11]、邓文武[17]和苏家妮[18]等人分别研究了同样的腔结构填充不同三能级和四能级原子系统的反射和透射特性，利用外加的驱动场等控制其吸收和色散，从而实现对反射和透射侧向位移的调控。本文用稳定相位法，计算了倒Y型原子气体填充的腔结构的反射和透射侧向位移，并分析了探测场失谐量、腔厚度对反射和透射率以及侧向位移的作用。

1 原子系统介绍

1.1 模型

频率为ω1的探测光，从真空（介质0）斜入射到由厚度为d1的腔壁（介质1）和厚度为d2的腔体（介质2）组成的腔结构，发生反射和透射如图1所示，其中反射和透射光相对于入射光分别产生了侧向位移Dr和Dt。介质0、1和2的介电常数分别为ε0、ε1和ε2，假设所有介质都是非磁性的，磁导率分别为μ0=μ1=μ2=1。根据特征矩阵法[19]，首先将腔结构分别三层：两层腔壁和一层腔体，将每层入射光和反射、透射光之间的电场和磁场分量关系可以表示为：

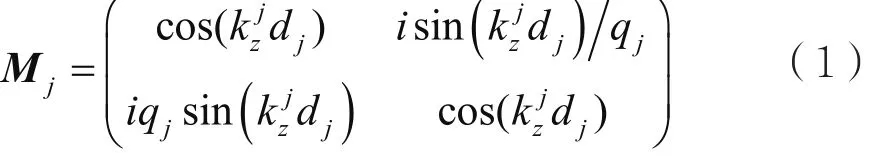
式中，两层腔壁的厚度和介电常数相同，即M3=M1。根据总特征矩阵的元素Qjk（j为行数，k为列数），可以计算得到反射系数r和透射系数t为

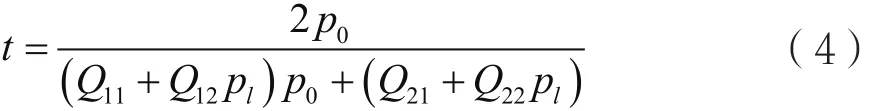
p的下标0和l分别代表入射和透射介质。由于腔结构放置在真空中，当垂直（Transverse Electric，TE）偏振光入射时，当平行（Transverse Magnetic，TM）偏振光入射时，其中为入射角θ。本文只研究了TE偏振光入射时的情况，TM的研究方法和TE的相同。

图1 线偏振光从真空斜入射到原子系统时，反射和透射侧向位移示意图

1.2 倒Y型四能级原子腔体

腔体填充的是如图2所示的四能级原子气体，在弱探测场E1的作用下，原子能实现从|1〉能级跃迁到|2〉能级，其中拉比频率（djk为态|j〉和态|k〉之间电偶极矩的2Ω矩1=阵E为约化普朗克常数）；在耦合场E0的作用下，原子能实现从|0〉能级跃迁到|2〉能级，其中拉比频率在泵浦场E2的作用下，原子能实现从|2〉能级跃迁到|3〉能级，其中拉比频率其中ω0、ω1和ω2分别为耦合、探测和泵浦场的频率，Δ0、Δ1和Δ2为能级间原子跃迁频率与电磁场频率之间的失谐量，γ0、γ1、γ2和γ3分别为能级之间原子跃迁的辐射衰变常数。

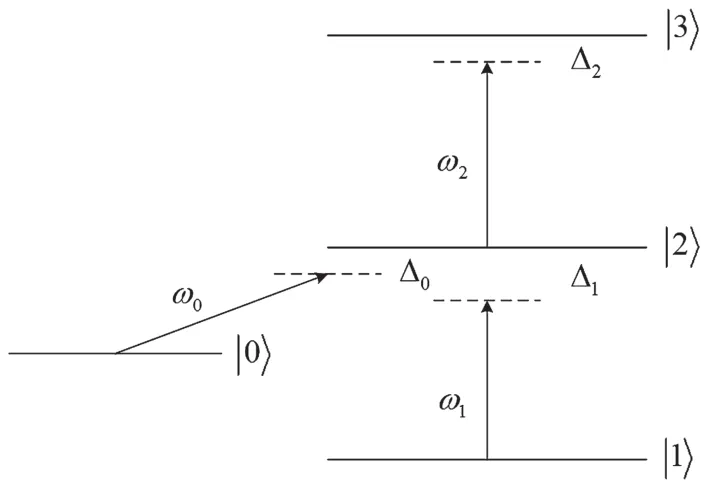
图2 倒Y型四能级原子能级示意图

倒Y型四能级原子的相互作用哈密顿量[20]：

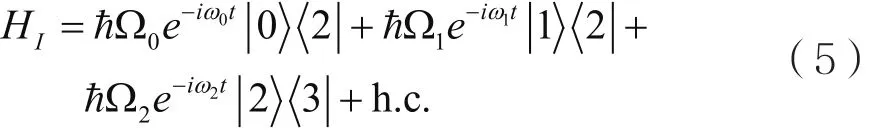
当耦合场和泵浦场都比探测场强很多的情况下，即几乎所有原子位于基态|1〉时，假设密度矩阵元ρ20和ρ23约等于0，将探测场的密度矩阵元只保留到最低阶，近似得到：

其中

极化率为：

受相干场的作用，根据式（3）和式（4）计算得到的反射系数和透射系数，用稳态相位法计算该结构的反射光和透射光的侧向位移Dr和Dt为

2 仿真实验

首先，取γ0=0.2γ，γ1=γ2=0.1γ，γ3=0，Ω0=3.5γ，Ω1=γ，Ω2=5.5γ，研究了耦合场和泵浦场共振时，探测场的失谐量对倒Y型原子系统吸收（Im（ρ12））和色散（Re（ρ12））的影响（见图3）。该情况下有两个吸收峰，当失谐量取为-5γ和5γ之间时，原子系统的吸收将近为0，即发生了电磁诱导透明；在吸收峰处，即当失谐量取6.5γ时，原子系统的色散将近为0，发生了电磁诱导吸收。本文主要仿真了这两种特殊情况的反射和透射侧向位移曲线。

取Δ1/γ=0，即探测场共振且发生电磁诱导透明时，腔壁厚度d1=0.2 μm，腔体厚度d2=2 μm，ε2=2.22，β=γ，其中γ=109Hz其他参数和图3中相同，反射率、透射率以及反射、透射侧向位移曲线（见图4、图5）。在反射率取最值时，反射侧向位移取到了最值，反射侧向位移有正值也有负值；透射率取最小值时，透射侧向位移取到了正向最大值。探测场共振时，透射场侧向位移一直为正；反射场最大侧向位移是负值，能达到-28λ。

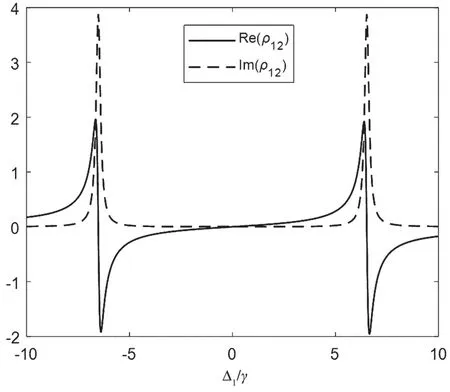
图3 原子系统的色散（实线）和吸收（虚线）随失谐量Δ1/γ 变化曲线

图4 Δ1/γ=0，原子系统的反射（实线）和透射率（虚线）随入射角变化曲线

图5 Δ1/γ=0，原子系统的反射（实线）和透射侧向位移（虚线）随入射角变化曲线

改变失谐量Δ1/γ=6.5，即探测场非共振且发生电磁诱导吸收时，其他参数不变和图4、图5中相同，反射率、透射率以及反射、透射侧向位移曲线（见图6、图7）。此时由于电磁诱导吸收，透射率几乎为0，反射率值也变小，透射和反射侧向位移都随入射角变化，两者的最值相近，和电磁诱导透明时的相比，侧向位移都变小了。改变腔体厚度d2=9 μm，其他参数和图4中相同，反射、透射侧向位移曲线，如图8所示。电磁诱导吸收时，改变腔体厚度，反射和透射的侧向位移分别趋向全部为负值和正值，和图7相比，该情况的位移最值也更大。

图6 Δ1/γ=6.5，原子系统的反射（实线）和透射率（虚线）随入射角变化曲线

图7 Δ1/γ=6.5，原子系统的反射（实线）和透射侧向位移（虚线）随入射角变化曲线

图8 d2=9 μm且Δ1/γ=6.5，原子系统的反射（实线）和透射率（虚线）随入射角变化曲线

3 结 语

本文通过控制原子气体的相关参数来调节腔体的介电常数，再结合腔壁、腔体的厚度和入射角等，能实现对腔结构横向位移的调控，比传统方法（直接调节介质本身的材料参数）更灵活、快捷。通过取不同失谐量，控制原子系统的吸收和色散，实现电磁诱导透明和电磁诱导吸收之间的切换，研究这两种不同情况下的反射和透射侧向位移。在原子系统无吸收和色散时，即电磁诱导透明，位移的最值位置和反射、透射率的最值位置相同；改变失谐量，

在原子系统无色散但有吸收时，即电磁诱导吸收，透射率为0，发生全反射，其反射和透射侧向位移比电磁诱导透明的小。调整腔厚度，可以实现对反射和透射率侧向位移的增强。