基于处理转发器的卫星跳频通信系统性能研究*

户凌志，张海勇，韩 东

（海军大连舰艇学院信息系统系，辽宁 大连 116018）

0 引 言

卫星通信具有覆盖范围广，通信距离远；频带宽，容量大；组网灵活等优点，是打赢现代化战争，夺取信息控制权的重要手段。但是，由于卫星暴露在空间轨道，易受到敌方的有意干扰，而导致通信链路被破坏，甚至整个卫星通信网络陷入瘫痪[1]。为了保证通信的可靠，必须采用高效的抗干扰技术。而采用处理转发器的卫星跳频通信系统，将星上处理（On-board Processing，OBP）与跳频技术（Frequency Hopping，FH）相结合，具有良好的抗干扰能力，是各国军事卫星通信抗干扰技术发展的重点[2]。因此，对处理转发卫星跳频通信系统的研究具有一定的现实意义。

目前，国内对处理转发卫星跳频通信系统的研究相对较少。文献[3]分析了不同干扰方式对卫星跳频通信上行链路的干扰效果，得出梳状谱干扰效果最佳的结论；文献[4]分析了跟踪干扰对卫星跳频通信的干扰椭圆，给出了最基本的干扰机设计诀窍。但是以上研究都未考虑处理转发器对通信链路的影响，而导致系统性能分析不够精确，为了保证处理转发卫星跳频通信系统的合理使用，以最大限度发挥其抗干扰能力，需要对其系统性能进行精确的分析。

1 基于处理转发器的卫星链路分析

1.1 处理转发器的工作原理与特性

处理转发器又称为再生式转发器，它可以对接收到的上行频率信号，经过一系列的星上处理，再通过下行频率转发给地球接收站，其工作原理如图1所示。

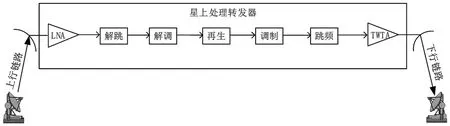
图1 处理转发器工作流程示意图

处理转发器对接收到的上行链路信号，经过低噪放大后，进行解跳得到中频信号，然后将中频信号送入解调器，解调为基带信号，再通过再生处理对信号加以增强，随后，将处理后的基带信号再重新调制到下行载波频率上，进行再跳频，最后通过末级功率放大器对信号进行放大，转发至下行链路地球站接收。

由于处理转发器通过对信号进行星上解调和再生，可以去除上行链路中的噪声及干扰，而不会随信号转移到下行链路，从而提高了整个传输链路的通信质量；而且可以通过星上处理，避免末级功率放大器的非线性影响而导致的功率掠夺及交调干扰，提高了星上功率资源的利用率[5]。

1.2 卫星通信链路分析

研究处理转发卫星跳频通信系统的传输性能，首先要研究卫星的通信链路。而星上处理转发器主要采用数字信号的传输[6]，通常以误比特率表示通信链路的性能。以下变量加方括号表示取10lg（）计算。

上行链路是指信号从地球站发射到卫星接收的链路。设地球站的有效全向辐射功率（Effective Isotropic Radiated Power，EIRP）为EIRPE，与输出功率PT及发射天线增益GT有关，计算如下：

式中LFT为发射天线馈线损耗。设卫星转发器接收增益为GR，则接收机输入端载波功率为：

其中，Lu为上行链路损耗，由上行大气损耗、上行自由空间损耗及其他损耗组成，如果链路中存在降雨，还需要补充降雨损耗。

已知卫星接收系统等效噪声温度Ts及有效噪声带宽Bn，则上行噪声功率Nu=kTsBn，噪声功率谱密度为其中Bn与滤波器滚降系数α，信息速率Rb,编码效率Cr,以及调制因子M有关，关系如下：

则上行链路载噪比为：

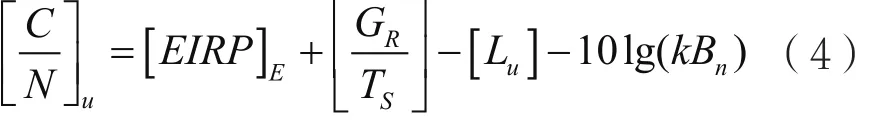
式中，GR/TS为卫星接收品质因数，衡量卫星接收能力的重要指标。载波功率可以表示为Cu=Eb*Rb，则上行每比特能量与噪声功率密度比可表示为：

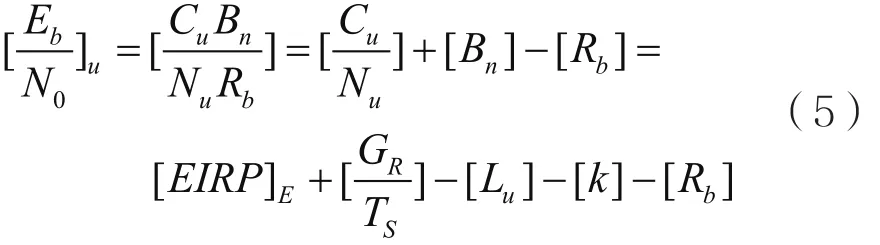
其中，k为玻尔兹曼常数，[k]=-228.6 dBW/(K·Hz)。误比特率Pb是[Eb/N0]的函数，与具体的调制方式有关。以二进制频移键控（Binary Frequency-Shift Keying，BFSK）为例，在高斯信道的条件下，采用非相干解调的上行链路误比特率为：

同理，可以求得下行链路的误比特率。下行链路是指信号由卫星发射给地球站的链路。设卫星有效全向辐射功率为EIRPs，下行链路衰减为Ld，同上行链路一样，由下行大气损耗、下行自由空间损耗及其他损耗等组成，下行链路载噪比为[8]：

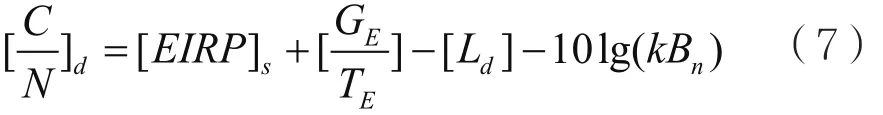
式中，GE/TE为地球站接收品质因数。则下行每比特能量与噪声功率密度比可表示为：

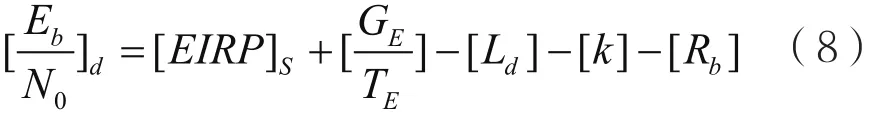
同样，对于采用BFSK调制，经非相干解调后的下行误比特率为：

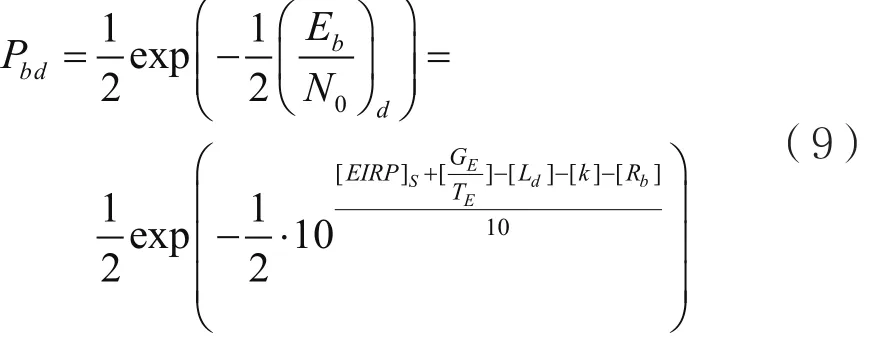
由于采用星上处理转发，经过星上再生处理，上行链路的噪声和干扰不会影响到下行链路，只会在星上解调时引起误码。上行链路的噪声以误码的形式传递到下行链路，所以，全链路的总误比特率由上、下行链路的误比特率共同决定[9]，工程上可通过以下公式计算：

具体的系统误比特率需要根据具体的调制解调方式而确定。

2 卫星跳频通信系统性能分析

2.1 系统的工作原理

卫星跳频通信是使窄带调制信号的载波在较宽带宽上按一定规律随机跳变，从而对干扰信号的躲避，达到抗干扰的效果。这种跳变规律又称为跳频图案，由一组伪随机码控制[10]。跳频通信系统基本工作原理如图2所示。

图2 卫星跳频通信系统基本工作原理

在地面发射站中，先将信息码调制为带宽为Bm的调制信号，然后用PN码控制频率合成器输出不同频率的载波对调制信号在带宽BC上以跳频周期Th的时间间隔进行跳变，形成跳频信号，再由发射机经上变频、放大经上行链路发送给卫星。定义跳频增益GP为跳频带宽BC与信息速率Rb的比值，即GP=BC/Rb，这样定义的好处是可以使GP与调制方式与编码体制无关[2]。

卫星采用星上处理转发器，对接收到的跳频信号进行解跳、解调，再生，调制，跳频，然后经过下变频、放大经下行链路转发给地面接收站。

在接收站中，通过同步电路对接收到跳频信号进行捕获分析，使本地产生与发射端相同跳频图案，对接收的跳频信号进行解跳，然后解调恢复出信息码。

在卫星跳频通信系统中，主要采用的调制方式为多进制频移键控（Multi-digit Frequency-Shift Keying，MFSK）和差分相移键控（Differential Phase-Shift Keying，DPSK）。其中MFSK的M为调制因子，表示调制进制数，例如，当M取4时，即4FSK，表示四进制频移键控；同理8FSK表示八进制频移键控。由于保持相位的相干性非常困难，通常采用非相干解调。

2.2 干扰条件下的系统性能

对于MFSK调制的跳频系统（FH/MFSK），在高斯信道的条件下，非相干接收的误比特率可由文献[11]得到：

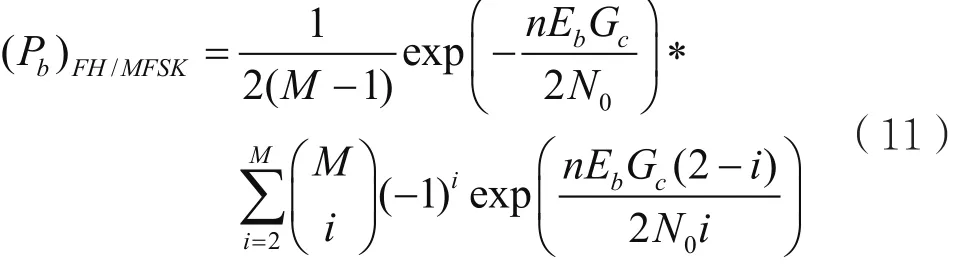
其中，n=log2M，Gc为编码增益。若链路中存在干扰，其实质上相当于链路中引起的附加噪声，设干扰功率为J，干扰功率谱密度为Nj，此时噪声功率谱密度由N0变为Nt=N0+Nj。则干扰环境下的系统误比特率为：

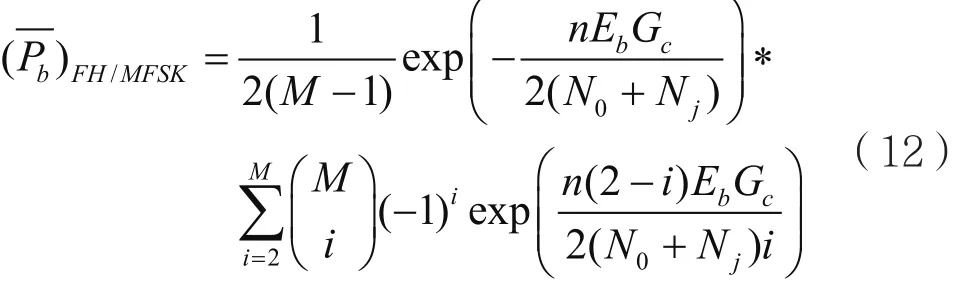
信号功率为P，与信息速率有如下关系：

已知干扰功率与信号功率的比值称为干信比（Jamming to Signal Ratio，JSR），则误比特率与干信比JSR=J/P的关系如下：

由2.1节讨论可知，处理转发卫星跳频通信链路性能是由上、下行链路误比特率共同决定，可以得MFSK卫星跳频通信系统的链路总误比特率，表达式为：

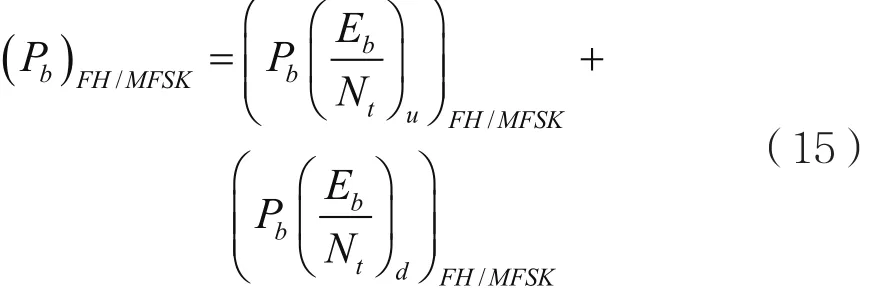
式中，当链路中无干扰时，Nt=N0；存在干扰时，Nt=N0+Nj。由已知系统的相关参数，带入式（5）、式（8）得到计算结果，将结果带入式（15），即可得FH/MFSK卫星通信链路总误比特率。

对于DPSK的卫星跳频系统（FH/DPSK），在高斯信道下的非相干解调误比特率为[12]：

同理，在存在干扰的环境下，则DPSK调制的跳频系统的平均误比特率为：

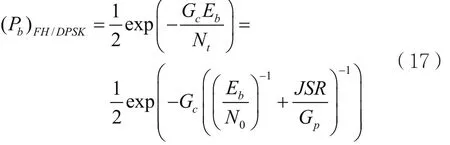
因此，DPSK调制的卫星跳频通信系统的链路总误比特率可表示为：

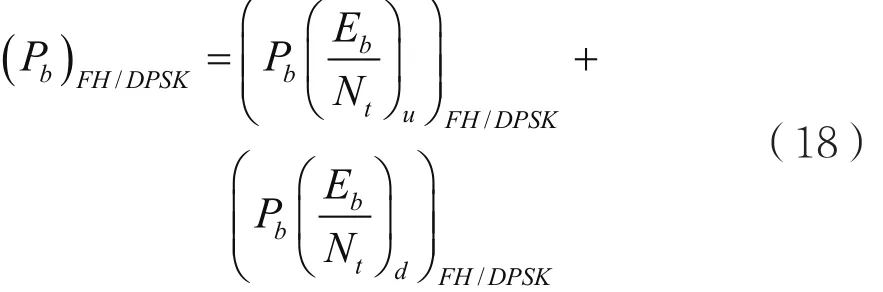
3 仿真及分析

为了分析处理转发卫星跳频通信系统的抗干扰性能，下面分别对采用MFSK及DPSK调制方式的卫星跳频通信系统在未受干扰和受不同程度干扰的条件下进行仿真。设系统采用R3/4及RS（204，188）级联编码，编码增益为5 dB，使3.6 kbit/s的数据在400 MHz的带宽上进行跳频传输，可计算跳频增益为50.5 dB，系统误比特率要求Pb≤10-6。首先分析系统在无人为干扰时，采用DPSK及MFSK在M=2，4，8的情况下，系统误比特率随信噪比的变化情况，仿真结果如图3所示。

图3 不同信噪比下的系统误比特率曲线图

从图3可以看出，当系统未受干扰时，随着信噪比的增加，系统的误比特率逐渐减小，系统的性能也逐渐提高；采用不同调制方式，系统的传输性能不同，分别采用BFSK，4FSK、8FSK和DPSK调制方式时，达到门限误比特率所需的信噪比分别为12.58 dB，9.73 dB，8.29 dB和9.58 dB，则系统性能DPSK与4FSK相近，且高于BFSK低于8FSK；对于MFSK调制，随着M的增加，系统的误比特率逐渐减小，所以多进制的频移键控能够改善系统的性能。

当链路中存在干扰时，图4、图5、图6分别给出了干扰信号功率比（JSR）为30 dB、35 dB和40 dB情况下，不同调制方式的系统误比特率仿真曲线图。

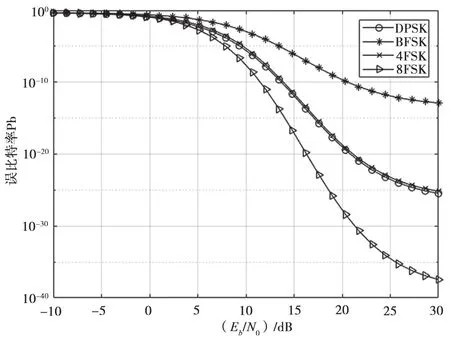
图4 JSR=30 dB的系统误比特率曲线图

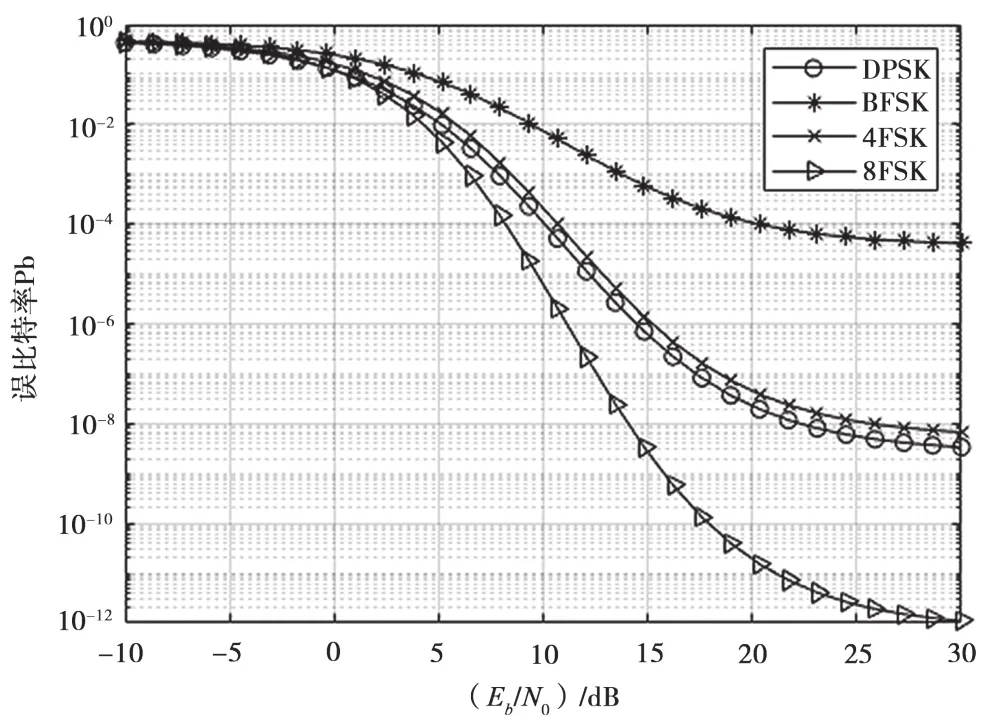
图5 JSR=35 dB的系统误比特率曲线图

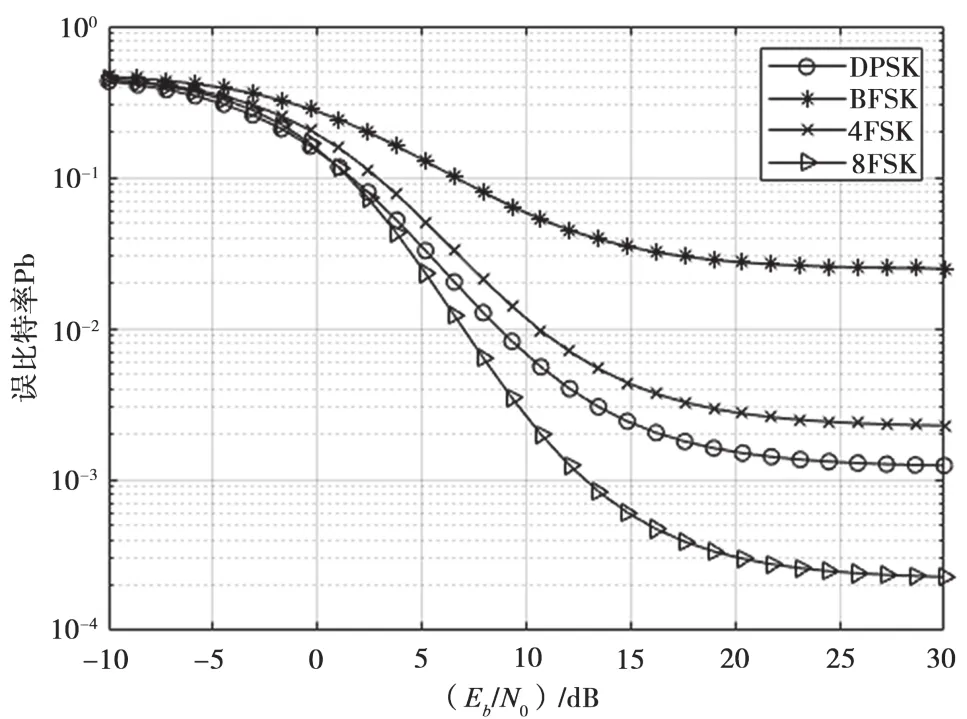
图6 JSR=40 dB的系统误比特率曲线图

从图4、图5、图6中可以看出，系统误比特率随着信噪比的增大而逐渐减小，系统性能逐渐升高；当干信比为30 dB时，采用BFSK，4FSK，8FSK及DPSK调制方式下的系统信噪比门限分别为14.83 dB，10.69 dB，9.31 dB和10.69 dB；当干信比为35 dB时，采用4FSK调制方式的系统的门限信噪比相比JSR=30 dB时系统的门限信噪比提高了4.14 dB，DPSK也提高了2.76，而8FSK仅提高1.38 dB，而采用BFSK调制，系统误比特率与信噪比无关，始终大于4×105，无法正常通信；当JSR=40 dB时，无论MFSK还是DPSK调制误比特率始终大于门限值，通信被严重干扰。

4 结 语

本文对基于再生式处理转发器的卫星跳频通信系统性能进行了研究，首先根据处理转发器的工作原理与特性，推导了基于星上再生处理转发的卫星通信链路误比特率计算表达式，然后结合跳频技术，分析了卫星跳频通信系统的工作原理并对在干扰条件下的系统误比特率表达式进行修正，最后对在不同调制方式下的卫星跳频通信系统性能进行仿真。

仿真结果表明，采用不同的调制方式，系统的抗干扰性能不同，采用8FSK调制的系统抗干扰能力最强，其次是DPSK和4FSK，BFSK最弱，因此，可以采用高进制数的MFSK调制使系统获得较好的抗干扰性能；当系统受到干扰时，随着干扰噪声功率增加，系统误比特率逐渐增大，系统性能明显下降，当干扰过大，单纯的增加信号功率无法改善系统的误比特率，此时可以采用如静默、突发等人为手段来抵御干扰。