基于动态矩阵模糊PID算法的工业锅炉温度控制优化研究

郭福雁，郭 蕊，王心怡

（天津城建大学控制与机械工程学院，天津300384）

温度是工业生产中最常见的控制参数之一，尤其在许多工业系统中，温度的控制直接影响产品的质量以及设备运行的安全性和经济性，对生产效率的提高和能耗的降低也至关重要.因为实际的工业锅炉温度控制是一个比较复杂的控制系统，具有抗干扰能力弱、延迟大、惯性大、对精度要求高等特点.目前，主要采用的是传统的PID 控制方法，但这种控制方法不但具有调整时间长、超调量大等缺点，而且其控制效果不佳，参数不能调整[1].本文针对锅炉温度控制系统延迟大和惯性大、参数变化难以控制等特点，提出了一种新型的控制方法——基于动态矩阵的模糊PID 控制系统.该方法利用动态矩阵算法并结合模糊算法，实现对传统PID 控制系统的优化，从而使PID 参数得到调整[2].通过对传统PID 控制系统、模糊PID 控制系统和动态矩阵模糊PID 控制系统进行仿真对比分析可证明，采用动态矩阵模糊PID 控制系统对锅炉温度进行控制，不仅可以有效解决系统的非线性、时变性和不确定性等问题，还能达到较好的控制效果，从而降低生产能耗.

1 锅炉温度控制系统分析

1.1 过程分析

锅炉温度控制主要通过热电偶传感器检测锅炉温度，系统接收到的温度信号经A/D 转换后送至PLC控制系统.依据这些数据，PLC 做出相应的判断：当锅炉的温度升高时，对其进行加热；当锅炉保持恒温状态时，PID 算法用于控制温度以满足输出要求，与此同时，PLC 将数据传到PC，PC 接收和显示报警[3].锅炉温度控制系统如图1 所示.

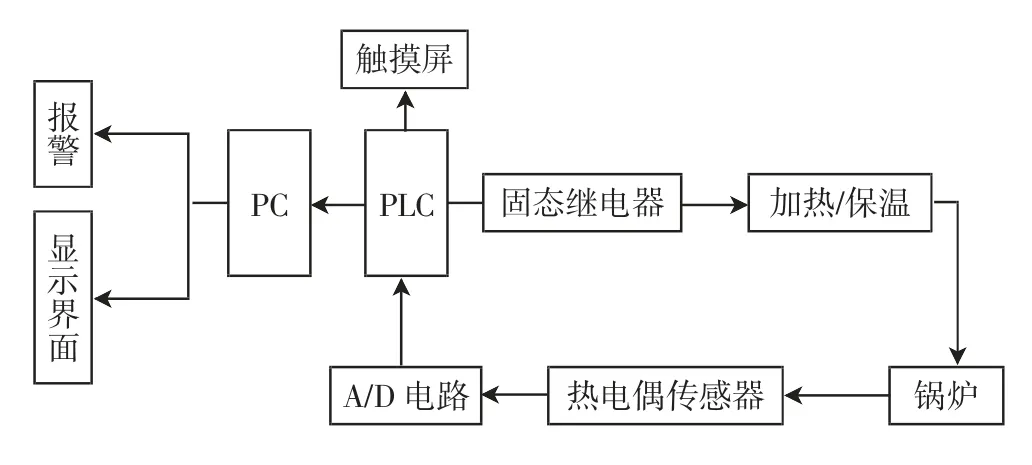
图1 锅炉温度控制系统

1.2 数学模型的建立

锅炉温度控制系统传递函数如下[4]

式中：K 为放大系数；T 为时间常数；τ 为传递滞后常数.

在单位阶跃信号的作用下，锅炉温度控制系统的响应曲线如图2 所示.

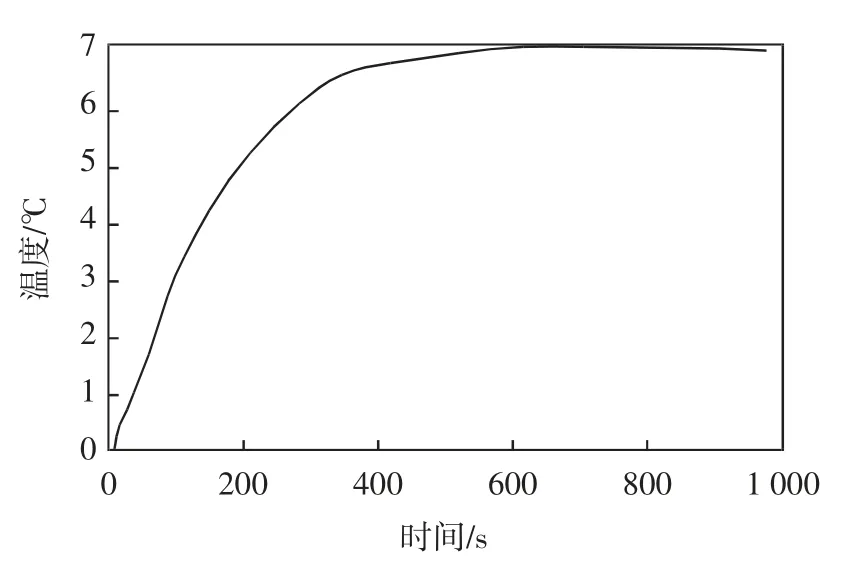
图2 锅炉温度系统的响应曲线

由图2 中曲线可以得到锅炉温度控制系统的数学模型为

2 模糊PID 控制系统

2.1 传统PID控制原理及缺陷

传统PID 算法是将偏差的比例、积分、和微分进行线性组合构成控制量，并控制被控对象.传统PID控制原理如图3 所示.

PID 控制系统是一个线性控制系统，通过比较参考r（t）和实际输出c（t）来控制偏差，其偏差公式如下

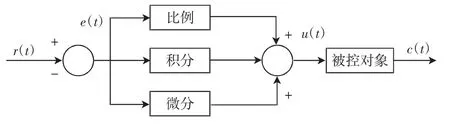
图3 传统PID控制原理

其数学模型如下

可见，传统PID 控制因其原理简单易懂、操作方便、可靠性高、适应性强等特点，一般多用于线性系统中.但是实际系统大多是非线性的，若使用传统PID 控制，选择PID 控制系数的最佳组合比例很困难，难以对参数进行积分和微分.根据传递函数使用Simulink构建传统PID 锅炉温度控制系统，经过多次仿真后，KP，KI和KD的匹配系数确定为0.24，0.065，1.0.但是，PID 参数是固定的，一旦确定不能改变，很难建立精确的系统模型，难以达到锅炉温度控制系统对精度的要求，从而使系统的抗干扰能力差、各方面性能不稳定、控制效果不佳.

2.2 模糊PID控制原理

2.2.1 系统总体架构

为了解决传统PID 的缺陷，本文在传统PID 系统上设计了模糊PID 控制系统.基于PID 算法，温度误差E 和温度误差变化率EC为输入，对E 和EC模糊化，通过模糊推理调整参数来实现不同时间的误差和误差变化率对PID 参数整定的条件，然后通过控制环节获取输出.

2.2.2 模糊化

输入变量选择温度误差E 和温度误差变化率EC，输出为KP、KI、KD，建立模糊规则表KP、KI、KD.输入和输出的隶属度值域均为[-3，3].使用离散法可分成不同的级别[-3，-2，-1，0，1，2，3]，对应模糊子集的设置，也以负大（NB）、负中（NM）、负小（NS）、零（Z）、正小（PS）、正中（PM）和正大（PB）为基础，类似地设置输出量，模糊子集也是NB、NM、NS、Z、PS、PM 和PB.

2.2.3 PID 参数整定原则

对于不同的E 和EC，控制过程中的参数KP，KI，KD，要求应符合以下规则：

（1）当|E|值越大时，应该采取较大的KP较小的KD，这样系统会达到更快的响应速度；

（2）当|E|值为中等时，应采用较小的KP且适当的KI和KD，这样系统就会获得更小的超调；

（3）当|E|数较小时，应采取较大的KP和KI且为了防止在平衡点附近发生震荡要采用适当的KI，这样系统会达到良好的稳定性能.

2.2.4 建立模糊控制规则表

温度误差和温度误差变化率被用作模糊控制系统的两个输入，三个输出为PID 控制系统的参数KP、KI和KD，这三个参数的模糊控制规则如表1-3 所示.

表1 KP模糊控制规则

表2 KI模糊控制规则

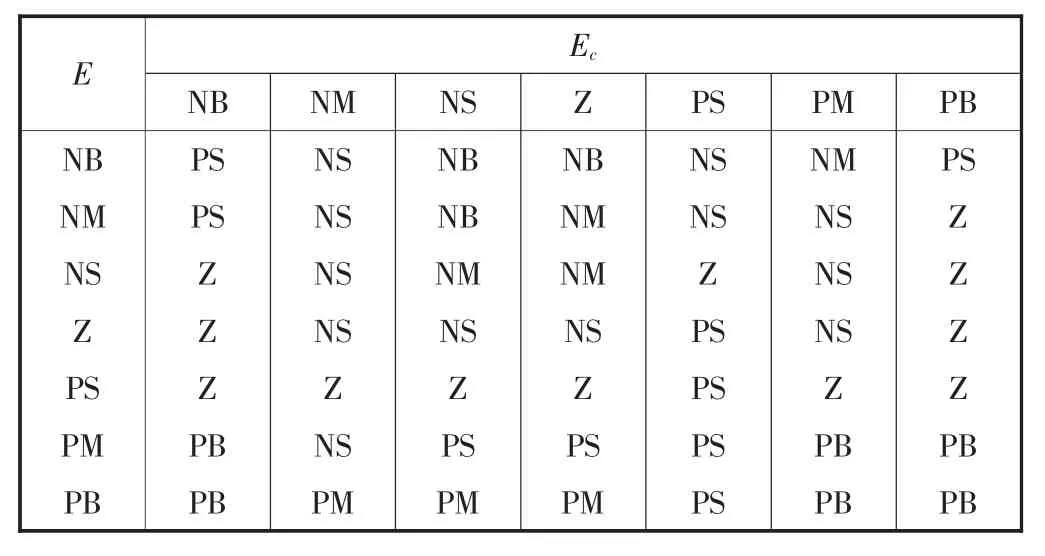
表3 KD模糊控制规则

模糊PID 锅炉温度控制系统是在传统的PID 控制的基础上引入模糊算法，当改变温度误差和温度误差变化率时，PID 参数也随之改变[5-6].此时，模糊PID控制系统中KP、KI和KD这三个输出量的论域均为[-3，3]，与预设参数的对比结果为：12.2，46.15，0.86.若输出变量没有被处理就加在预设的PID 参数上，就会使得有些比值偏大.为了避免这种现象，在叠加之前就需要进行处理，经过多次系数迭代后，KP、KI和KD的匹配系数确定为0.38，0.025，0.45.

实际上，即使采用模糊PID 控制系统，其参数通常是在分析的基础上再结合经验得出的，无法进行误差校正.想得到一组更加精确的参数，应建立精确的数学模型，本文引入动态矩阵算法.

3 动态矩阵模糊PID 控制系统

3.1 动态矩阵模糊PID控制原理

动态矩阵是一种系统优化算法，基于计算机控制，通过预测模型，统计过去和现在的偏差，预测未来的偏差得到最佳输入.动态矩阵模糊PID 控制系统如图4 所示.

图4 动态矩阵模糊PID 控制系统

3.2 预测模型建模

阶跃响应模型是动态矩阵控制的预测模型，通过此模型预测未来的输出，并且其对象特性为动态响应系数b1…bp、bp表示足够接近稳态值的系数，p 表示模式时域长度.如果在某一时刻k-i（k＞i）输入u（k-i），则相应输出的输出贡献为

如果所有k-i（i=1，2，3，…，n）时间都有输入则控制对象未来每个时间的输出预测值有

由于之前的输入是已知的，所以要分开之前的输入对将来输入的贡献，可得

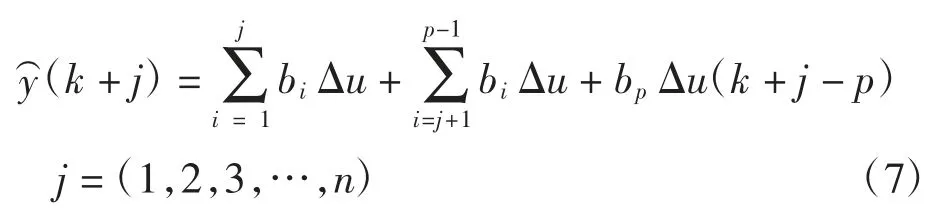
后面两项表示之前输入对输出的n 步预测，记为

即

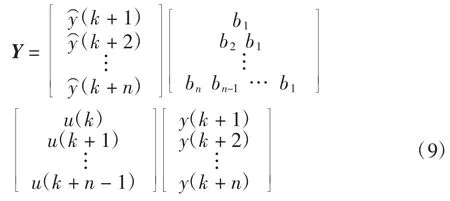
3.3 滚动优化

该算法通过使用优化准则来确定Δu（k）的最小值.为了使系统在下一时刻输出尽可能接近期望值的温度值，经简化计算后公式如下.

令W = [w（k + 1），w（k + 2），…，w（k + n）]T，则表示为

通过滚动优化使得将来某个时间段内某个性能指标被最小化，通过在某个采样时间进行采样和输出来完成，从而进行新的预测，优化和校正，这样可以防止系统因为干扰信号的存在而失去控制.所以，滚动优化这个过程需要反复的在线操作，每次需要优化的目标也会随时间的变化而变化[7-9].

3.4 误差校正

在实际操作中可能会出现模型不匹配和环境干扰等未知因素的影响，预测值可能会偏离实际值，所以要及时使用实时信息进行修正，以免以后的工作建立在错误的基础上[10].

由于一次只实施第一个Δu（k）进行控制，因此可以使用以下公式来预测将来的输出，即

式中：Yp表示下一时刻系统输出的温度的有效值；b 表示阶跃响应值.由于实际输出不一定与时间受控后的预测输出相同，这样就会导致预测错误，然后误差被加权修正用作未来其他时间的预测，其校正后公式为

4 MATLAB 仿真

为了比较传统PID 控制系统、模糊PID 控制系统和动态矩阵模糊PID 控制系统的控制效果，本文对以上三种控制方法做了仿真实验，设定输入温度为25 ℃，仿真时间为200 s 时将温度改为23 ℃，仿真时间为1 000 s，三种控制方式的对比仿真曲线图5所示.

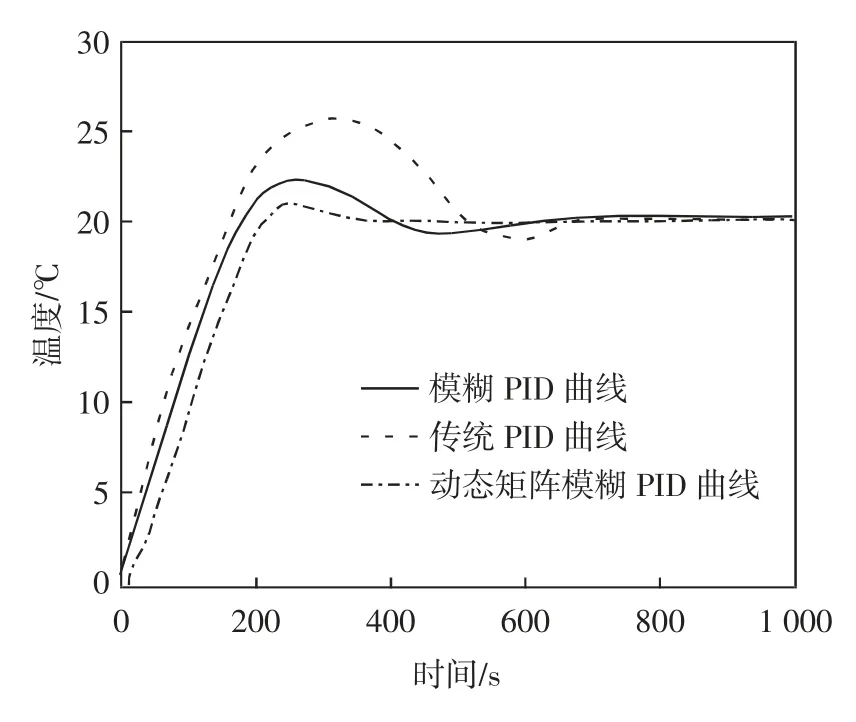
图5 三种控制方式的对比仿真曲线

根据图5，针对以上三种系统仿真结果比较其动态响应特性，得到三个系统的超调量、稳定时间和上升时间三个动态参数的比较，动态参数比较如表4所示.

表4 动态参数比较

4.1 传统PID 系统仿真

通过图5 仿真曲线和表4 可以看出，传统PID 锅炉温度控制系统的曲线波动比较大，性能不稳定，在经过2 次波动之后才达到稳定状态，超调量为25%，上升时间大约需要300 s，达到稳定时间需要750 s.传统的PID 虽然抗干扰的能力较强，但是无法控制延迟大的对象.

4.2 模糊PID 系统仿真

在MATLAB 的模糊逻辑工具箱中构建锅炉温度模糊控制系统，使用Simulink 构建模糊PID 温度控制系统，参数根据PID 控制的调节规则确定[11-12]，PID 参数如表5 所示，仿真图如图5 所示.

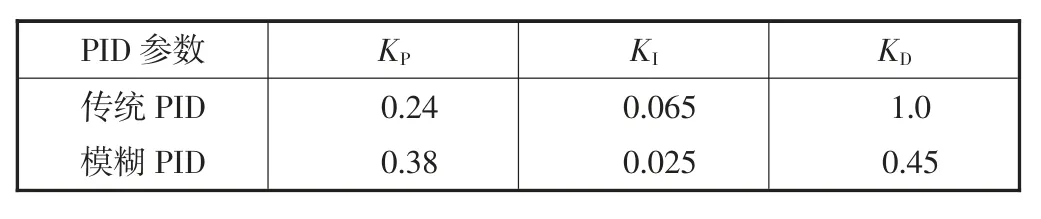
表5 PID 参数

从图5 和表4 中可以看出，模糊PID 曲线相对于传统PID 要平稳的多，超调量为5.3%，相较于传统PID 超调量减小了许多，上升时间260 s，达到稳定时间需要620 s，可见引进模糊算法后，系统的稳定性和延迟性得到了有效的改善.

4.3 动态矩阵模糊PID 系统仿真

动态矩阵模糊PID 控制系统将动态矩阵算法和模糊PID 控制结合.系统将初始时期的输出与下一个时期输出作比较，从而可以得出差值然后通过误差校正来调整，这样的变化规律可以预示未来的变化.在每一个周期中，差值都在不断地发生变化，可以实现在线的误差校正，从而可以保证所建立的模型的精确性，仿真图即图5.

由仿真图5 和表4 可知，动态矩阵模糊PID 曲线的性能指标很好，几乎没有震荡就达到了平衡状态，超调量为0.15%，仅需400 s 就达到了稳定状态，上升时间需要230 s.由此可以得出，模糊PID 控制的各性能指标会比传统PID 控制的效果更佳，而动态矩阵模糊PID 控制的效果更加的优化于模糊PID.通过仿真表明，动态矩阵模糊PID 控制更加稳定，各性能明显得到了很大的提升.

5 结 语

本文针对传统PID 和模糊PID 控制存在的缺陷，提出了利用动态矩阵算法对参数进行优化的方法，并设计了动态矩阵模糊PID 控制系统.与传统的PID 锅炉温度控制系统和模糊PID 控制系统相比，动态矩阵模糊PID 锅炉温度控制系统具有更好的控制效果，并通过MATLAB/SIMULINK 的仿真结果表明，该方法具有简单、计算量小、参数可以自动调整的优点，并且其调整规则简单、实用性强，满足了系统对精度要求高的需求.其既具有常规PID 的优点，又具有模糊控制的自适应性和灵活性，且控制效果也更加优越.同时，在不影响系统响应精度和稳定性的情况下，系统的大滞后问题得到改善，该方法具有一定的应用价值.