内摩擦角对冻融岩石损伤本构模型的影响探讨

袁 超，张慧梅，孟祥振，杨更社，吴禄源

内摩擦角对冻融岩石损伤本构模型的影响探讨

袁 超1，张慧梅2，孟祥振1，杨更社1，吴禄源3

(1. 西安科技大学建筑与土木工程学院，陕西 西安 710054；2. 西安科技大学理学院，陕西 西安 710054；3. 中国矿业大学深部岩土与地下工程国家重点实验室，江苏 徐州 221116)

基于Weibull随机分布和损伤力学理论，从岩石变形全过程的特点入手，选用Drucker-Prager准则，建立能反映冻融岩石各变形阶段特征的损伤本构模型。通过冻融砂岩常规三轴压缩试验，运用Mohr应力圆，获得不同冻融循环次数下砂岩的黏聚力和内摩擦角；由模型理论曲线与冻融砂岩试验曲线对比分析，验证模型的合理性；通过变动内摩擦角，分析摩擦角对模型是否存在影响。结果表明：基于Drucker-Prager准则获得的理论曲线与试验曲线吻合较好，验证了模型的合理性；内摩擦角对分布变量的影响较大，且是线性关系，但对损伤本构模型没有影响或影响不大。研究成果对岩石本构关系的建立有较好的参考价值。

Drucker-Prager准则；损伤本构模型；黏聚力；内摩擦角；冻融实验

自然界岩石随着自身所处应力场及其他环境的变化而变化，其内部或多或少地出现损伤，利用损伤理论来研究含有缺陷的岩石材料，已被认为是最有效的研究方法之一。

目前，对岩石应力应变关系的描述成果众多。单因素情况下，韩建新等[1]基于岩体强度参数随最大塑性主应变的增加而逐渐演化这一力学行为，采用广义Hoek-Brown强度准则，通过理论推导给出岩体应变软化行为模型；黄海峰等[2]为了反映岩石应变软化现象，基于Weibull随机分布，假定岩石微元强度服从Drucker-Prager准则，结合连续损伤理论，建立岩石统计损伤软化模型；张德等[3]通过引入修正Mohr-Coulomb屈服准则来描述冻土微元强度破坏准则，假设微元强度服从Weibull随机分布，并根据统计学和连续损伤力学理论，建立能反映破损全过程的损伤本构模型；王苏生等[4]基于Mohr-Coulomb破坏准则以及岩石微元强度服从Weibull函数随机分布假设，构建了统计损伤本构模型；房智恒[5]在Mohr-Coulomb准则及岩石微元强度服从对数正态随机分布的基础上，结合岩石三轴应力应变试验曲线，建立了能反应岩石破裂全过程的三维损伤本构模型；熊良宵等[6]简述了Mohr- Coulomb强度准则、抛物线型Mohr强度准则和双曲线型Mohr强度准则，并采用3种高应力下岩石的真三轴试验结果对这3种强度准则进行对比分析；LI Xiang等[7]、CHEN Xin等[8]通过引进岩石微元强度，利用其服从随机分布并根据Lemaitre应变等价原理，建立了能反映岩石应变软化过程的损伤统计本构模型。多因素情况下，虞松涛等[9]、张慧梅等[10]基于统计强度理论及损伤力学原理，分别以Hoek-Brown准则和Mises准则为岩石强度准则，构建考虑温度与荷载共同作用的岩石损伤演化；ZHOU Shuwei等[11]、HUANG Shibing等[12]和张慧梅等[13]采用静态弹性模量法对岩石冻融损伤进行了表征，以Drucker-Prager准则为岩石强度准则，并假设微单元强度满足Weibull分布，通过统计理论得到加载损伤，在此基础上，推导出冻融和载荷作用下的统计损伤本构方程。

对以上岩石损伤本构模型中微元强度准则的选取主要有Drucker-Prager准则、Mohr-Coulomb准则、Mises准则及Hoek-Brown准则，而Hoek-Brown是一种经验强度准则；Mises准则则是Drucker-Prager准则简化形式；Mohr-Coulomb准则相对较为保守。在各种准则之中，大多涉及到内摩擦角及黏聚力等参数的确定，内摩擦角及黏聚力的准确性确定，影响准则的正确性，从而可能影响到损伤本构模型的合理性；以往本构模型并没有对内摩擦角等参数进行探讨。基于此，笔者基于Weibull分布和损伤力学理论，选用Drucker-Prager准则，通过设定不同内摩擦角，应用于岩石微元强度准则，进而分析内摩擦角对冻融岩石损伤本构模型的影响。

1 冻融岩石受荷微元强度的度量

根据岩石在细观结构上的非均质性，其内部微元体力学性质的分布具有随机性，岩石未损伤部分连续加载时，导致其内部受荷损伤也是一个连续过程，当假定岩石微元强度服从Weibull随机分布时，受荷损伤变量d可表示为：

式中为岩石微元强度随机分布变量；0、为模型参数。

岩石受荷损伤变量能否更好地反映一定条件下岩石的损伤变形特征，其关键之处在于岩石微元强度的合理度量。

为此，假定冻融岩石受荷时微元强度随机分布变量服从Drucker-Prager准则，则可表示为：

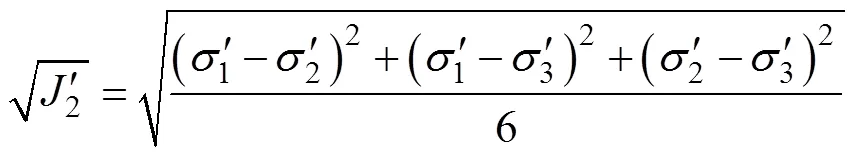
2 本构模型及其模型参数的确定

2.1 本构模型的建立

岩石应变软化变形全过程可分为压密、线弹性、塑性硬化变形、应变软化、完全破坏5个阶段，因此，在建立岩石损伤模型时要充分考虑岩石上述各个阶段的变形特征。首先作如下假设：

①岩石内部的微元破坏，其力学性质在宏观上为各向同性。

③未损伤部分服从广义胡克定律，并依据岩石物理参数泊松比的意义以及岩石各部分的变形协调关系，等围压下可得：

基于上述假定，通过岩石各部分微观受力与几何条件分析可得：

式中、1、2分别为岩石总面积、未损伤面积和损伤面积，因此=1+2，其中损伤面积由冻融损伤面积n和受荷损伤面积d组成。

岩石微元破坏损伤是由冻融损伤、受荷损伤两部分组成，此时定义岩石冻融、受荷总损伤变量表达式为：

单独从岩石面积方面考虑，冻融损伤变量n可定义为冻融损伤面积与整体面积的比值；受荷损伤变量d可定义为受荷损伤面积与去除冻融损伤面积后整体面积(–n)的比值，因此可得：

由式(7)—式(8)并结合②、③假定可得轴向方向的损伤本构模型：

2.2 模型参数的确定

将式(1)、式(8)代入式(9)可得：

将该条件代入式(10)得模型参数的一个表达式：

同时，应力应变峰值点处还应该满足条件

将该条件应用于式(10)可得模型参数的另一个表达式：

本文假定了冻融岩石受荷时微元强度随机分布变量服从Drucker-Prager准则，结合②、③假定，可得：

因此，由式(13)可得：

联立式(11)、式(12)、式(14)可确定模型参数和0，即：

3 计算实例与讨论

为了探讨内摩擦角对岩石损伤本构模型是否有影响，先进行了红砂岩冻融循环实验和常规三轴压缩力学特性试验。试验先将红砂岩加工成直径50 mm、高100 mm的圆柱体试样，并对试件进行注水达到真空饱和；冻融循环温度为–20~20℃，对饱和试样进行冻融0次、5次、10次、20次及40次实验，之后对红砂岩进行围压0 MPa、2 MPa及4 MPa三轴压缩试验。试验得到了不同围压及不同冻融作用下岩石的力学参数，如表1所示。

将式(13)、式(15)、式(16)代入式(10)之后，利用表1和表2试验数据，可得基于Drucker-Prager准则冻融受荷岩石本构模型理论曲线，如图1所示，以此来证明基于Drucker-Prager准则建立的模型合理性。由图1可知，基于Drucker-Prager准则建立的模型获得的理论曲线和试验曲线吻合较好，能够较好的反映岩石各变形阶段特征。

表1 不同冻融循环及围压下红砂岩的力学参数

表2 不同冻融循环次数下的内摩擦角和黏聚力

4 内摩擦角的影响分析

将非冻融及冻融后砂岩内摩擦角分别选取0°、45°、90°，分别获得不同冻融循环情况下的分布变量曲线、不同围压和不同冻融循环次数与峰值点处分布变量值的关系曲线以及损伤本构模型理论曲线，如图2—图5所示。由此可知：

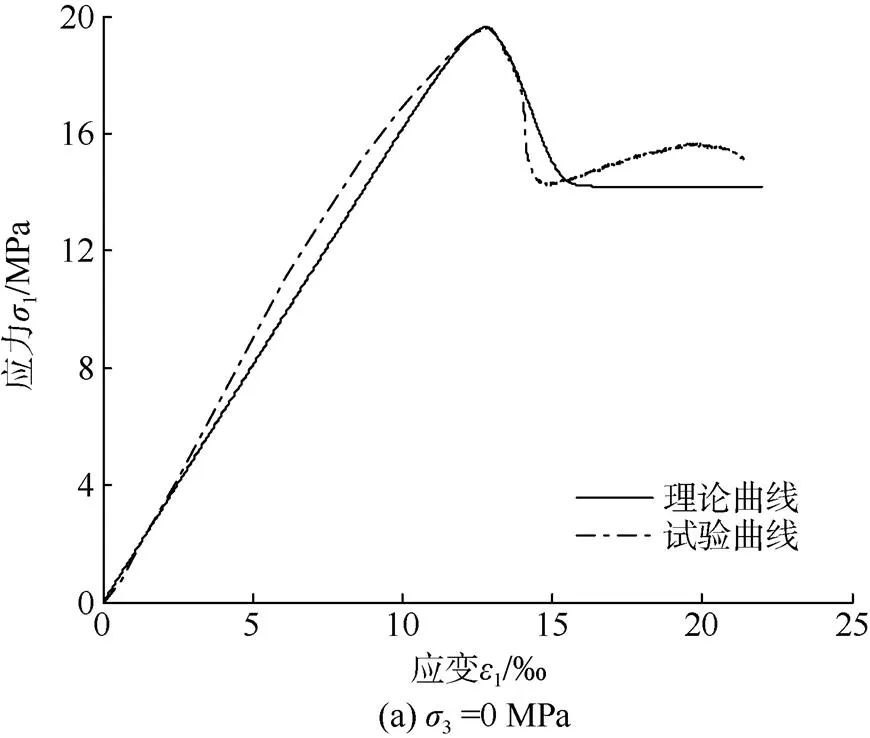
图2 内摩擦角对分布变量F的影响

图3 不同围压下内摩擦角对分布变量值的影响(n=1)

a.内摩擦角对分布变量的影响较大，且呈线性关系，同一应变下，随着内摩擦角的增大，分布变量逐步增大，但增大的幅度有所减缓。

b.相同的内摩擦角下，随着围压的增大，峰值点处的分布变量值逐渐增大，但增大速率减缓；同一围压下，峰值点处的分布变量值随着内摩擦角的增大而增大，且增大速率减缓。说明了围压和内摩擦角随着自身的增大对分布变量值的影响度降低。

图4 不同冻融循环下内摩擦角对分布变量值的影响(σ3=2 MPa)

图5 内摩擦角对本构模型的影响

c.相同的内摩擦角下，随着冻融循环次数的增大，峰值点处的分布变量值逐渐减小，曲线趋于平缓，说明冻融循环随着次数的增大对分布变量值的影响度降低。

d.内摩擦角的变动对基于Drucker-Prager准则确定的损伤本构模型没有影响，或影响不大。因此，为了能够建立更好的反映岩石变形破坏全过程的本构模型，可自由选取内摩擦角的取值，或不考虑内摩擦角的影响。

5 结论

a.采用弹性模量对岩石冻融损伤进行了表征，通过Drucker-Prager准则来描述冻融岩石微元强度破坏，以此建立了能反映冻融岩石破损全过程的损伤本构模型。由冻融砂岩常规三轴压缩试验，运用Mohr应力圆，获得不同冻融循环下砂岩的黏聚力和内摩擦角；模型理论曲线与冻融砂岩试验曲线对比分析，基于Drucker-Prager准则获得的理论曲线与试验曲线吻合较好，验证了模型的合理性。

b.内摩擦角对分布变量的影响较大，且是线性关系，同一应变下，随着内摩擦角的增加，分布变量逐步增大，但增大的幅度有所减缓；相同的内摩擦角下，围压及冻融循环对峰值点处的分布变量值的影响度随自身的增加有所弱化。

c.探讨了不同内摩擦角对岩石损伤本构模型的影响。内摩擦角的变动对基于Drucker-Prager准则确定的损伤本构模型没有影响，或影响不大。因此，为了能够建立更好的反映岩石变形破坏全过程的本构模型，可自由选取内摩擦角的取值，或不考虑内摩擦角。

[1] 韩建新，李术才，汪雷，等. 基于广义Hoek-Brown强度准则的岩体应变软化行为模型[J]. 中南大学学报(自然科学版)，2013，44(11)：4702–4706. HAN Jianxin，LI Shucai，WANG Lei，et al. Model for strain- softening behavior of rock mass based on generalized Hoek- Brown strength criterion[J]. Journal of Central South University(Natural Science)，2013，44(11)：4702–4706.

[2] 黄海峰，巨能攀，蓝康文，等. 岩石统计损伤软化模型及其参数反演[J]. 长江科学院院报，2018，35(6)：102–106. HUANG Haifeng，JU Nengpan，LAN Kangwen，et al. Statistical damage softening model for rock and back analysis of its parameters[J]. Journal of Yangtze River Scientific Research Institute，2018，35(6)：102–106.

[3] 张德，刘恩龙，刘星炎，等. 基于修正Mohr–Coulomb屈服准则的冻结砂土损伤本构模型[J]. 岩石力学与工程学报，2018，37(4)：978–986. ZHANG De，LIU Enlong，LIU Xingyan，et al. A damage constitutive model for frozen sandy soils based on modified Mohr-Coulomb yield criterion[J]. Chinese Journal of Rock Mechanics and Engineering，2018，37(4)：978–986.

[4] 王苏生，徐卫亚，王伟，等. 岩石统计损伤本构模型与试验[J]. 河海大学学报(自然科学版)，2017，45(5)：464–470. WANG Susheng，XU Weiya，WANG Wei，et al. The statistical damage constitutive model of rocks and its experiment[J]. Journal of Hohai University(Natural Sciences)，2017，45(5)： 464–470.

[5] 房智恒. 基于Mohr-Coulomb准则的岩石损伤本构模型研究[J]. 矿业工程研究，2017，32(1)：7–13. FANG Zhiheng. Rock damage constitutive model based on Mohr-Coulomb criterion[J]. Mineral Engineering Research，2017，32(1)：7–13.

[6] 熊良宵，虞利军. 三种Mohr强度准则的对比分析[J]. 长江科学院院报，2016，33(4)：81–85. XIONG Liangxiao，YU Lijun. Comparative study of three Mohr strength criteria[J]. Journal of Yangtze River Scientific Research Institute，2016，33(4)：81–85.

[7] LI Xiang，CAO Wengui，SU Yonghua. A statistical damage constitutive model for softening behavior of rocks[J]. Engineering Geology，2012，143/144：1–17.

[8] CHEN Xin，LIAO Zhihong，PENG Xi. Deformability characteristics of jointed rock masses under uniaxial compression[J]. International Journal of Mining Sciences and Technology，2012，22(2)：213–221.

[9] 虞松涛，邓红卫，张亚南. 温度与围压作用下的岩石损伤本构关系研究[J]. 铁道科学与工程学报，2018，15(4)：893–901. YU Songtao，DENG Hongwei，ZHANG Yanan. The constitutive relationship of rock damage considering the effect of temperature and confining pressure[J]. Journal of Railway Science and Engineering，2018，15(4)：893–901.

[10] 张慧梅，雷利娜，杨更社. 温度与荷载作用下岩石损伤模型[J]. 岩石力学与工程学报，2014，33(增刊2)：3391–3396. ZHANG Huimei，LEI Lina，YANG Gengshe. Damage model of rock under temperature and load[J]. Chinese Journal of Rock Mechanics and Engineering，2014，33(S2)：3391–3396.

[11] ZHOU Shuwei，XIA Caichu，ZHAO Haibin，et al. Statistical damage constitutive model for rocks subjected to cyclic stress and cyclic temperature[J]. Acta Geophysica，2017，65(5)：893–906.

[12] HUANG Shibing，LIU Quansheng，CHENG Aiping，et al. A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application[J]. Cold Regions Science and Technology，2018，145：142–150.

[13] 张慧梅，孟祥振，彭川，等. 岩石变形全过程冻融损伤模型及其参数[J]. 西安科技大学学报，2018，38(2)：260–265. ZHANG Huimei，MENG Xiangzhen，PENG Chuan，et al. freeze-thaw damage model and parameters rock deformation in whole process[J]. Journal of Xi’an University of Science and Technology，2018，38(2)：260–265.

Influence of internal friction angle on damage constitutive model of freeze-thaw rock

YUAN Chao1, ZHANG Huimei2, MENG Xiangzhen1, YANG Gengshe1, WU Luyuan3

(1. College of Architecture and Civil Engineering, Xi’an University of Science and Technology, Xi’an 710054, China; 2. Department of Mechanics, Xi’an University of Science and Technology,Xi’an 710054, China; 3. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou 221116, China)

Based on Weibull random distribution and damage mechanics theory, starting from the characteristics of rock deformation process, the Drucker-Prager criterion was used to establish a damage constitutive model that can reflect the characteristics of rock various deformation stages. Through the conventional triaxial compression test of frozen-thawed sandstone, the Mohr stress circle was used to obtain the cohesion and internal friction angle of the sandstone under different freeze-thaw cycles. The model theoretical curve and the test curve of freeze-thaw sandstone were compared to verify the model rationality. By varying the internal friction angle, whether the friction angle has an effect on the model was analyzed. The results showed that the theoretical curve obtained by the Drucker-Prager criterion agreed well with the experimental curve, which verified the rationality of the model. The internal friction angle had big influence on the distribution variable and was linear, but had no effect on the damage constitutive model or had little effect. The research results have a good reference value for the establishment of rock constitutive relations.

Drucker-Prager criterion; damage constitutive model; cohesion; internal friction angle; freeze-thaw test

TU443

A

10.3969/j.issn.1001-1986.2019.04.021

1001-1986(2019)04-0138-06

2019-01-22

国家自然科学基金资助项目(11172232，51774231，11872299，41772333)；陕西省自然科学基础研究计划资助项目(2018JQ4026)；中国矿业大学未来科学家“双一流”计划资助项目(2019WLKXJ076)

National Natural Science Foundation of China(11172232，51774231，11872299，41772333)；Natural Science Basic Research Plan of Shaanxi Province of China(2018JQ4026)；Future Scientists Program of “Double First Rate” of China University of Mining and Technology(2019WLKXJ076)

袁超，1989年生，男，陕西铜川人，博士，研究方向为岩土力学与工程应用. E-mail：yuanchao828@163.com

袁超，张慧梅，孟祥振，等. 内摩擦角对冻融岩石损伤本构模型的影响探讨[J]. 煤田地质与勘探，2019，47(4)：138–143.

YUAN Chao，ZHANG Huimei，MENG Xiangzhen，et al. Influence of internal friction angle on damage constitutive model of freeze-thaw rock[J]. Coal Geology & Exploration，2019，47(4)：138–143.

(责任编辑 周建军)