双曲线二维O tsu阈值分割算法*
赵 恒 安维胜 杨 陶
(西南交通大学机械工程学院 成都 610031)
1 引言
图像分割是图像处理中的一个重要步骤,在于从图像中提取出关键信息进行后续处理。随着图像处理技术在现实生活中的应用增多,其在国内外的研究也不断深入。图像分割方法主要包括阈值法、区域法、边缘检测法,以及基于图论、基于聚类等特定理论的分割方法[1]。阈值分割算法又包括Otsu 法[2~3],基于熵的阈值分割法[4~5],基于遗传算法[6]等阈值分割法。其中,Otsu法(最大类间方差法)因简单高效性,广泛应用于机器视觉,模式识别等领域。Otsu法根据图像一维信息选取阈值,对受到噪声干扰,无明显双峰的图像,分割结果不理想。
二维Otsu自动阈值分割算法(传统二维直分法)考虑图像灰度和空间邻域信息,使分割结果准确性和抗噪声能力得到提升[7]。但传统二维直分法搜索阈值运算量较大,实时性差[8]。文献[9~10]改进的二维阈值分割算法,使运行时间降低,提升了抗噪能力,但确定阈值时仍然忽略了一部分像素信息,分割精度降低。文献[11~12]中提出并改进的二维直方图区域斜分算法(二维直方图斜分法),虽然阈值附近像素信息没有忽略,但区域宽度由人工确定,导致噪声和边缘信息误划分。文献[13]改进的二维Otsu曲线阈值分割法,直接将噪声划分到目标背景区域,阈值搜索时间和抗噪能力都不够理想。文献[14]的二维直方图区域叉分法,用两条通过阈值点与灰度级轴分别成α,β角的直线对二维直方图进行区域分割。对于不同图像的二维直方图,最佳α,β角匹配参数难以选取,运算效率和自适应性都较差。
本文提出新的区域划分双曲线二维Otsu阈值分割算法。考虑到分割质量和实时性,结合Sobel边缘检测算子提取出图像边缘点[15],选取边缘点信息并用三次样条曲线拟合法拟合选取的边缘信息得到两条曲线[16],将图像目标背景像素和最佳阈值限制在两条曲线之间的带状区域,两条曲线外的区域视为噪声,对于噪声采用文献[17]基于小概率策略的方法进行处理,最后对图像进行阈值分割。
2 传统二维Otsu直分法

并且:

整个二维直方图区域若任意选取一个阈值(s,t),则将二维直方图划分为四个区域,如图1所示。A,B为噪声区域,D0,D1为两类目标背景区域。ω0、ω1分别代表D0,D1的概率:
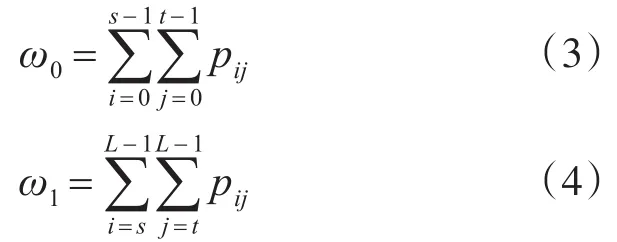
μ0,μ1分别为代表D0,D1区域对应的均值矢量,则:

图像的总均值矢量:
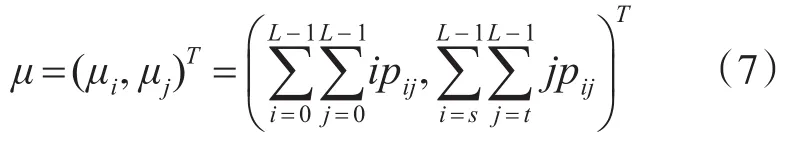
忽略A,B区域的概率:

则类间离散度矩阵表示为
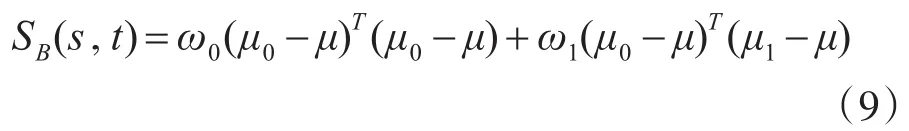
离散度矩阵的迹作为离散度测算,因此,最佳阈值的选取原则为

3 本文算法的实现
3.1 双曲线截距方式
如图2(b)所示,可以看到图像像素带状区域边缘轮廓呈不规则分布,实际图像像素在对角线上下波动,改进二维直方图斜分算法严格的用直线去进行分区并不合理,并且其两条直线之间的距离由人为确定,使得噪声和目标背景像素难以正确划分,此分区方法存在缺陷。图像边缘点与其邻域均值的差异使得在二维直方图中,不同点(i,j)会沿对角线上下偏移,并且介于目标背景点和噪声点之间的区域[12]。基于这一特性用三次样条曲线拟合法分别拟合对角线上下边缘点为曲线,就可以更加精确地将目标背景和噪声进行分离。

图1 传统二维直方图直分
3.2 目标背景区域边界曲线拟合
用Sobel边缘检测算子检测图像得到边缘点在二维直方图中的坐标(m,n),并且按照对角线进行分类。若m>n,用于拟合上边界曲线;反之,用于拟合下边界曲线。定义灰度级水平T1=i+j,(T1=0,1,2,…,2L-2)。由于在二维直方图中边缘点可能在同一坐标点或者是同一灰度级水平T1多次出现,需对边缘信息进行筛选。当m>n时,相同灰度级水平T1有多个边缘点,取|m-n|值最大(即远离对角线最远)时的坐标点,将更多边缘信息归于目标背景;相同坐标下同时出现多个边缘点,选取一次坐标点。对筛选之后的边缘点坐标进行三次样条曲线拟合,从而得到上边界曲线S1;反之,同理可得下边界曲线S2。曲线拟合结果如图2(b)所示,图2(c)是其分区简化模型。两条曲线之间的灰色区域视为目标背景区域;灰色区域外的两个A区域共同归为噪声区。噪声在图像所占的概率较小,其邻域均值更加接近其真实像素,替换其灰度值为邻域均值,可提高算法抗噪性。
3.3 截距阈值分割
对改进的二维直方图采用穷举搜索的方法获得阈值点(s,t)(灰度级水平为s+t=T)进行阈值分割,算法实时性较差。对于改进的二维直方图斜分算法,任意像素点灰度级水平T1<T时,视为目标;反之视为背景。因此就可以将图像在灰度级水平T1进行截距阈值分割。将区域处理后的二维
灰度级水平的总概率P(T1),再进行阈值分割,可提高算直方图各个点的概率投影到对角线,并计算对角线上每个法实时性。当i+j=T1时:
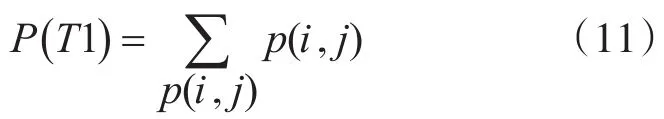
根据图2(d)分区简化模型,D0,D1分别为目标、背景,截距直线g+f=T为阈值。设ω0(T),μ0(T)以及ω1(T),μ1(T)分别代表D0,D1类的概率和两个灰度均值,μ代表总均值。从而有:

类间方差:
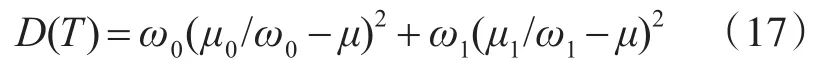


图2 本文区域划分方式
当类间方差最大时取得最佳截距阈值T*,即
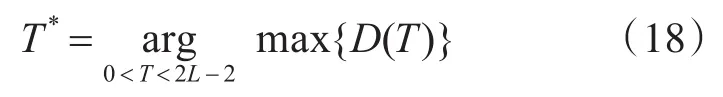
4 实验分析
本次实验设备为Intel i3 CPU@3.4GHz,4GB内存的Win7系统台式电脑,软件采用Matlab R2014b。测试的算法包括改进的传统的二维Otsu算法[9],改进的二维直方图区域斜分算法[12]以及本文的算法。对比的两种算法都是经过改进,相比于原算法性能大幅度提升的算法。测试内容包括测试算法的分割质量、时间对比和算法的抗噪性能。
4.1 分割质量与时间测试
图像分割质量通过图像区域内部均匀性(U)来进行说明[18]。区域内部均匀性主要用来描述图像分割所形成的区域内部相似程度。通常情况下,U值较大说明图像内部均匀性较高,图像分割质量好。

图3 无噪图像及其分割结果
本文对多张图像进行了测试,选取图3中几张图像作为示例说明各算法分割效果。图3(b)是三种算法对不同图像的分割结果,从分割结果中可以看出改进传统二维直方图效果较差,本文算法结果和改进的二维直方图斜分算法效果差异较小。仔细观察图像细节,可以看到本文在边缘细节分割效果比改进二维直方图斜分好。表1是三种算法分割结果的U值及其时间对比。在区域划分时各自采取了不同的策略,导致同一图像的分割结果有所差异。本文算法的U值最高,说明本文算法图像分割质量高。从表1中的算法耗时结果可以看出,本文算法和文献[12]算法速度比文献[9]算法大幅度加快,本文算法相比文献[12]稍慢,但保证了较高分割质量,耗时增加在允许的范围内。
其实从图2(c)中可以看出,边缘点沿对角线分布不规则,二维直方图对角线两端区域边缘点相比于其他区域更加靠近对角线,文献[12]也提到边缘介于噪声和目标背景之间,则可推知噪声也比其他区域更加靠近对角线。对不同图像噪声边缘分布情况差异较大,简单用直线进行分割,可能将边缘外的噪声误划分为目标背景,或者是将大量边缘信息划为噪声。本文双曲线自适应划分的方式,充分考虑了图像二维直方图分布不规则的特点,符合图像二维直方图实际分布情况。用该方式确定带状区域,增强了算法的自适应能力,而且用已经筛选过的较少的边缘信息进行拟合曲线,降低了边缘划分为噪声的可能性,使得大部分边缘信息能够归于目标背景区域获得更加精确的阈值,能够提高图像分割质量。
4.2 抗噪声性能测试
实际图像在拍摄传输存储过程中常会受到噪声干扰,在阈值分割时影响后续处理。但噪声强度一般不高,在某些对图像细节边缘要求较高的情况下,若对图像直接进行不同尺度的平滑滤波,将会导致图像细节边缘区域模糊,影响分割准确性,所以需对算法进行初始抗噪性能测试。本文同时对图3中无噪图像施加高斯噪声、椒盐噪声、乘性噪声混合的等强度为0.05的噪声进行测试。从图4的分割结果看,三种算法都能对含噪图像进行有效分割,但本文算法结果含噪点数量最少,分割效果更好。峰值信噪比(PSNR)[19]是衡量算法抗噪性能的量化指标,PSNR值越大代表算法的抗噪性能越好,可以对算法的图像分割抗噪性能进行客观的评价。从表2可以看出,本文算法的PSNR值较其他算法的分割结果高,与视觉效果一致。说明本文算法的抗噪能力较高。

图4 混合噪声图像分割结果

表2 各算法对混合噪声图像分割数据对比
5 结语
针对二维直方图直分和斜分算法存在的不足,本文提出双曲线二维Otsu阈值分割算法。通过边缘检测得到并筛选边缘信息,用两条根据边缘信息拟合的曲线对二维直方图进行重新分区,使得图像噪声、边缘和目标背景像素划分的更加精确,用小概率策略对噪声进行处理后,再对图像进行阈值分割。最后与改进传统二维直方图直分算法,改进二维直方图斜分算法进行实验对比分析。
实验结果表明:针对不同图像,本文算法分割质量和抗噪性能相比于二维直方图直分和斜分算法都有所提升;在运算速度上比二维直方图斜分算法稍慢,比传统二维直方图直分算法有大幅度提升。综合理论和实验数据,本文算法自适应能力强,鲁棒性好,能提高图像分割质量,有良好的抗噪能力,在较大程度上满足图像分割实时性要求,具备一定推广实用价值,可作为后续图像处理的基础。

