住房租赁市场监管的进化博弈分析
余孝军,何南昆
(贵州财经大学 数统学院,贵州 贵阳,550025)
随着我国城镇化的快速发展,各种住房需求叠加,导致住房租赁市场爆炸式发展。尽管各级政府采取了各种措施增加公租房和廉租房的供给,但远远不能满足城市人口的住房需求。为促进住房租赁市场的健康有序发展,各级政府出台了各种制度,对住房租赁市场进行规范。学者们也从不同角度对住房租赁市场进行了研究,吴晓[1]从承租人的视角对南京租房租赁市场进行了调研,认为成立住房租赁公司和加大廉租房的建设力度会完善租房租赁市场。黄燕芬等[2]通过对住房租赁市场的现状分析和对发达国家住房市场先进经验的总结,认为以“租购同权”促“租售并举”,是构建住房租赁市场长效机制的重要举措。叶剑平等[3]通过调查发现,不健全的住房租赁市场是造成住房销售市场与住房租赁市场不平衡的重要原因,加大政府的监管力度对于完善住房租赁市场,优化住房市场结构有着重要的意义。周建军等[4]构建了中央政府和地方政府之间的静态博弈模型,探讨了住房租赁市场发展缓慢的原因,在此基础上提出了促进住房租赁市场发展的建议。戴思龙[5]运用博弈理论构建了住房租赁市场各行为主体之间的博弈模型,通过对模型的分析,提出了解决目前市场上存在问题的管理建议。郑生钦等[6]构建了政府、消费者、企业的三方演化博弈模型,通过仿真模拟,得到了影响各博弈方演化的主要因素。本文认为住房租赁市场是住房市场的重要组成部分,对我国房地产市场的健康发展有着重要影响。为避免住房租赁市场的无序发展,有必要加强政府监管部门对住房租赁市场的监管。
本文将运用进化博弈理论探讨住房租赁市场监管问题。通过分析住房租赁市场中不同行为主体的行为选择,构建两类进化博弈模型,通过对博弈模型的分析,得到影响各行为主体策略选择的因素,提出规范住房租赁市场的合理建议。
1 房东群体间的进化博弈分析
进化博弈理论是将经典的非合作博弈论与生态学理论相结合,以有限理性群体为研究对象[7],采用动态分析方法将影响各博弈方行为的各种因素纳入模型,从系统论的角度研究了群体行为的演化趋势[8]。进化博弈理论提出后,在诸多领域得到了广泛的应用[9-12]。首先,运用进化博弈理论对房东群体间的行为进行分析。
1.1 模型构建
为分析方便,将房东群体(以下简称房东)简化为两个有限的个体:房东甲和房东乙,且都是有限理性的博弈方。假设房东在住房租赁市场中,有合规出租和违规出租两种策略,即按照相关的法律法规选择合规出租,或者是一味追求利益,不考虑租户情况,不遵守相关法律法规违规出租。假设房东合规出租时的收益为e,房东违规出租时的额外收益为f,房东违规出租时被监管部门发现后受到的处罚为g,房东违规出租被监管部门发现的概率为x(0≤x≤1)。显然,若博弈双方都采取违规出租策略时,一定会被监管部门发现。房东群体间博弈的收益矩阵如表1所示。
表1 房东群体间博弈的收益矩阵
Table 1 The payoff matrix of the game of landlords

房东甲 违规出租房东甲 合规出租房东乙 违规出租(e+f-g,e+f-g)(e+f-xg,e)房东乙 合规出租(e,e+f-xg)(e,e)
上述涉及的参数都为正数,博弈的均衡由参数e、f、g、xg的相对大小关系决定。
1.2 复制动态方程和进化稳定策略
接下来研究房东间博弈的动态调整过程,假设在房东群体间,选择违规出租策略的房东比例为y,则选择合规出租策略的房东比例为1-y。据此,房东选择违规出租和合规出租的期望收益分别为
则房东群体的平均期望收益为
由上述期望收益,可得房东选择违规出租策略时的复制动态方程为
(1)
易得,方程(1)有三个稳定点,即为
由进化博弈理论可知,进化稳定策略具有抗干扰性,即因偶然因素致使偏离均衡状态,但随着时间的推移会再次回复到原来的稳定状态。据此,可得如下三个命题:
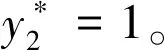
该命题说明,在房东选择违规出租策略时的额外收益大于其因违规行为而受到的处罚时,则房东将选择违规出租策略。即使最初时,所有房东都选择合规出租策略,但由于住房租赁市场监管制度缺失、监管部门处罚力度不够,致使房东选择违规出租策略时的收益大于风险,随着房东间的多次重复博弈,所有的房东一定都会选择违规出租策略。



该命题说明,在房东选择违规出租策略时的额外收益不仅小于合规出租的收益,而且得不偿失时,则房东群体中将没有人选择该策略。如果监管部门加大监管力度,大力查处违规出租行为,并对违规出租行为采取重罚政策时,那么违规出租行为将会大大减少,直至消失。此时,房东选择合规出租策略才是最好的策略。
2 房东群体与监管部门之间的进化博弈分析
由前面房东群体间的进化博弈模型,可知房东的收益及策略选择与监管部门的策略是相关的。下面,对房东群体与监管部门两个群体间的博弈进行分析。
2.1 模型及其复制动态方程
该博弈中有两个不同的群体,一个是住房房东群体,另一个是监管部门,假设双方都是有限理性的博弈方。先对博弈做以下假设:房东群体有合规出租和违规出租两种策略,监管部门有监管和不监管两种策略。房东选择合规出租策略时的成本为c1,收益为a1;房东采取违规出租策略时的成本为c2,收益为a2;房东选择违规出租策略时造成的社会不良影响量化为d,记为监管部门的损失;房东选择违规出租策略时一旦被监管部门查处,其所受处罚为b1,假设其处罚全部归监管部门所有;若监管部门不监管违规出租行为造成社会影响,将受到上级部门的处罚,值为b2;监管部门的监管成本为c。本节假设,只要监管部门进行监管,则一定能查处到房东的违规出租行为,所有参数皆为正数。综上,房东群体与监管部门之间博弈的收益矩阵如表2所示。
表2 房东和监管部门博弈的收益矩阵
Table 2 The payoff matrix of the landlord and the housing rental supervision department

监管部门 监管监管部门 不监管房东 合规出租(a1-c1,-c)(a1-c1,0)房东 违规出租(a2-c2-b1,b1-d-c)(a2-c2,-d-b2)
表2所示的收益矩阵是房东个体与监管部门个体之间的博弈收益矩阵,显然可知,此时博弈为非对称博弈。两个群体之间的每次博弈,其实质是在各自群体中随机选取一个成员进行博弈,两个群体间的博弈就是无数次这样的随机配对博弈,双方的策略学习及模仿都是局限在其所在群体之内,也就是说每个群体策略调整机制还是可以用复制动态方程来刻画。假设,房东群体中选择合规出租策略和违规出租策略的比例分别为p和1-p。监管部门选择监管策略和不监管策略的比例分别为q和1-q。则房东群体选择合规出租、违规出租时的期望收益分别为
u11=q(a1-c1)+(1-q)(a1-c1)=a1-c1,
u12=q(a2-c2-b1)+(1-q)(a2-c2)=a2-c2-qb1。
则对应的期望平均收益为
进而,可知房东选择合规出租策略时的复制动态方程为
(2)
同理,可得监管部门的复制动态方程为
(3)
2.2 进化博弈模型稳定性分析
FRIED[13]通过对雅可比矩阵局部稳定性的分析,得到了博弈均衡的稳定性,进而讨论博弈方的策略选择。系统的动态调整可以用方程(2)和(3)的联立方程组来刻画,即:
(4)
则方程组(4)对应的雅可比矩阵为

则,上面雅可比矩阵的行列式为
(1-2p)(1-2q)(a1-c1-a2+c2+b1q)(b1+b2-c-b1p-b2p)+b1(b1+b2)pq(1-p)(1-q)。
该雅可比矩阵的迹为
trJ=(1-2p)(a1-c1-a2+c2+b1q)+(1-2q)(b1+b2-c-b1p-b2p)。
1)当a1-c1>a2-c2且b1+b2 表3 情形 1 时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(-)(a1-c1-a2+c2)+(b1+b2-c)鞍点(1,0)(a1-c1-a2+c2)c(+)-(a1-c1-a2-c2)-c(-)稳定点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(+)(a1-c1-a2+c2+b1)-(b1+b2-c)(+)不稳定点(1,1)-(a1-c1-a2+c2+b1)c(-)-(a1-c1-a2+c2+b1)+c鞍点 命题4:当a1-c1>a2-c2且b1+b2 此命题说明,当房东选择违规出租策略时的利润小于选择合规出租策略时的利润,且监管部门查处违规出租行为的所得与因不监管行为所受的处罚之和小于监管部门的监管成本时。房东均愿意采取合规出租策略,监管部门更愿意采取不监管策略。 2)当a1-c1>a2-c2且b1+b2≥c时,方程组(4)有四个均衡点(0,0)、(0,1)、(1,0)、(1,1),则各均衡点对应的稳定性分析如表4所示。 表4 情形2时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(+)(a1-c1-a2+c2)+(b1+b2-c)(+)不稳定点(1,0)(a1-c1-a2+c2)c(+)-(a1-c1-a2-c2)-c(-)稳定点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(-)(a1-c1-a2+c2+b1)-(b1+b2-c)鞍点(1,1)-(a1-c1-a2+c2+b1)c(-)-(a1-c1-a2+c2+b1)+c鞍点 命题5:当a1-c1>a2-c2且b1+b2≥c时,(1,0)是方程组(4)的进化稳定策略。 此命题说明,当房东选择违规出租策略时的利润小于选择合规出租策略时的利润,且监管部门查处违规出租行为的所得与因不监管行为所受的处罚之和不小于监管部门的监管成本时。房东均愿意采取合规出租策略,监管部门更愿意采取不监管策略。 3)当a1-c1≤a2-c2≤a1-c1+b且b1+b2 表5 情形 3 时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(+)(a1-c1-a2+c2)+(b1+b2-c)(-)稳定点(1,0)(a1-c1-a2+c2)c(-)-(a1-c1-a2-c2)-c鞍点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(+)(a1-c1-a2+c2+b1)-(b1+b2-c)(+)不稳定点(1,1)-(a1-c1-a2+c2+b1)c(-)-(a1-c1-a2+c2+b1)+c鞍点 命题6:当a1-c1≤a2-c2≤a1-c1+b且b1+b2 此命题说明,当房东选择违规出租策略时的利润不低于采取合规出租策略时的利润,但不超过采取合规出租策略时的利润与被监管部门查处的处罚之和时,且监管部门监管查处违规出租行为所收获的处罚与因不监管行为所受的处罚之和小于其监管成本。房东均愿意采取违规出租策略,由于监管成本过高,监管部门宁愿选择不监管策略。 表6 情形4时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(-)(a1-c1-a2+c2)+(b1+b2-c)鞍点(1,0)(a1-c1-a2+c2)c(-)-(a1-c1-a2-c2)-c鞍点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(-)(a1-c1-a2+c2+b1)-(b1+b2-c)鞍点(1,1)-(a1-c1-a2+c2+b1)c(-)-(a1-c1-a2+c2+b1)+c鞍点(p∗,q∗)-c(b1+b2-c)(a1-c1-a2+c2)(a1-c1-a2+c2+b1)b1(b1+b2)(+)0中心点 命题7:当a1-c1≤a2-c2≤a1-c1+b1且b1+b2≥c时,(p*,q*)是方程组(4)的进化稳定策略。 5)当a1-c1+b1 表7 情形5时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(+)(a1-c1-a2+c2)+(b1+b2-c)(-)稳定点(1,0)(a1-c1-a2+c2)c(-)-(a1-c1-a2-c2)-c鞍点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(-)(a1-c1-a2+c2+b1)-(b1+b2-c)鞍点(1,1)-(a1-c1-a2+c2+b1)c(+)-(a1-c1-a2+c2+b1)+c(+)不稳定点 命题8:当a1-c1+b1 此命题说明,当房东选择违规出租策略时的利润大于选择合规出租策略时的利润与其被监管部门查处的处罚之和,且监管部门查处违规出租行为的所得与因不监管行为所受的处罚之和小于监管部门的监管成本时,房东必然选择违规出租策略,监管部门因监管成本过大,更愿意采取不监管策略。 6)当a1-c1+b1 表8 情形6时各均衡点的稳定性分析 均衡点detJ(符号)trJ(符号)稳定性(0,0)(a1-c1-a2+c2)(b1+b2-c)(-)(a1-c1-a2+c2)+(b1+b2-c)鞍点(1,0)(a1-c1-a2+c2)c(-)-(a1-c1-a2-c2)-c鞍点(0,1)-(a1-c1-a2+c2+b1)(b1+b2-c)(+)(a1-c1-a2+c2+b1)-(b1+b2-c)(-)稳定点(1,1)-(a1-c1-a2+c2+b1)c(+)-(a1-c1-a2+c2+b1)+c(+)不稳定点 命题9:当a1-c1+b1 此命题说明,当房东选择违规出租策略时的利润大于选择合规出租策略时的利润与其被监管部门查处的处罚之和,且监管部门查处违规出租行为的所得与因不监管行为所受的处罚之和大于监管部门的监管成本时,房东必然选择违规出租策略,监管部门因监管成本不高,且能够从监管中获得更多收益,因此其采取监管策略。 文章通过运用进化博弈理论,构建了两类住房租赁市场监管的博弈模型。通过分析,发现住房租赁市场监管博弈模型中博弈方的策略选择受到多种因素的相互制约。房东是否选择合规出租策略与其选择该策略时的利润、监管部门对违规出租行为的打击力度正相关;房东选择违规出租策略的概率与监管部门对违规出租行为的惩处力度成负相关,与选择该策略时获得的利润以及选择违规出租策略与获得的超额收益正相关。监管部门选择监管策略的概率与其监管成本、查处违规出租的处罚所得、不监管行为所受的处罚有关。其中,降低监管成本对加大监管力度并无明显作用,但增加监管成本将会打击监管部门的积极性,增大其选择不监管策略的概率,但是加大对监管部门不作为的惩处力度能有效加强监管工作的开展。 为促进住房租赁市场的健康有序发展,监管部门应建立健全的机制,加大对违规出租行为的打击力度,增大处罚力度,增大违规出租行为的成本。同时,出台政策扶持合规出租,增大其收益,降低其成本。政府应加强对住房租赁监管部门不作为的处罚力度,单纯依靠降低监管部门的监管成本并不一定会加强其监管力度。
Table 3 Stability analysis of equilibria at Case 1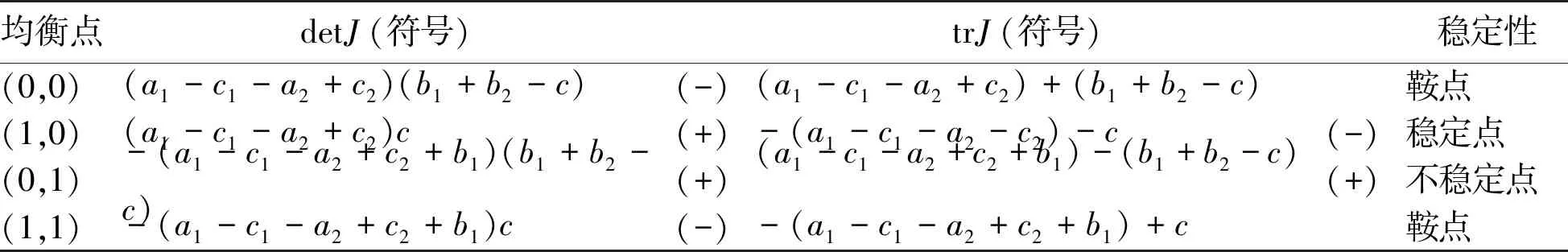
Table 4 Stability analysis of equilibria at Case 2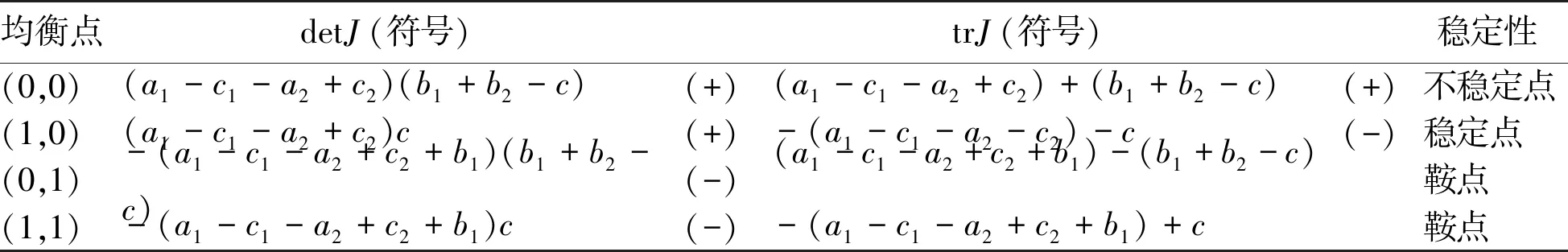
Table 5 Stability analysis of equilibria at Case 3
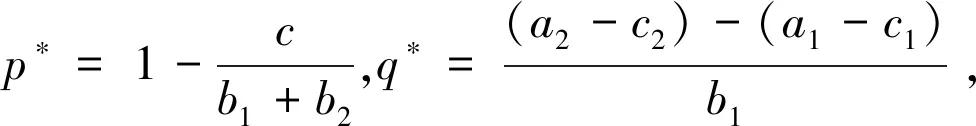
Table 6 Stability analysis of equilibria at Case 4

Table 7 Stability analysis of equilibria at Case 5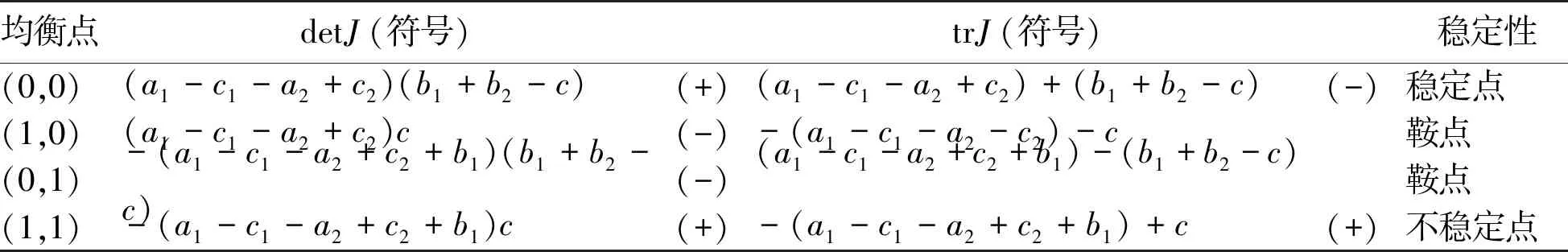
Table 8 Stability analysis of equilibria at Case 6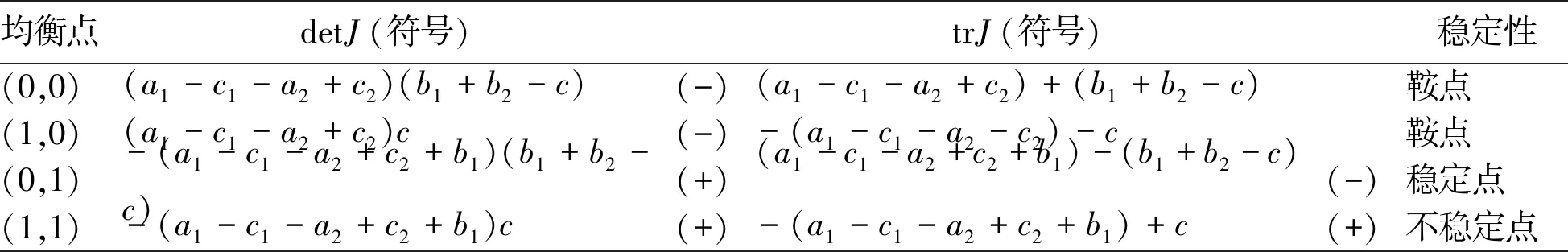
3 结论

