基于仿生微圆结构的汽车吸能盒耐撞性分析

白中浩 谭雯霄 张林伟 周存文

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

薄壁管以其优异的能量吸收特性和较小的质量，广泛应用于汽车吸能盒中[1]。在过去几十年中，研究人员运用仿真建模[2]、理论分析[3]和试验研究[4]对薄壁管的吸能特性进行了大量探索，结果表明，薄壁管的截面形状对能量吸收效率有显著的影响[5]。文献[6-8]对比了具有不同横截面的单胞薄壁管与多胞薄壁管的耐撞性，研究发现多胞薄壁管具有更优异的吸能特性，因此，近年来多胞薄壁管受到了研究人员的广泛关注。文献[9-10]对具有不同横截面的多胞薄壁管进行了理论分析，结果表明，不同类型的多胞薄壁管在压溃时具有不同的能量吸收特性，其原因主要为构成多胞薄壁管的不同类型肋板结构在压溃过程中所耗散的能量不同。由此可知，可通过研究肋板结构的吸能特性来提高多胞薄壁管的能量吸收效率。

为进一步研究薄壁管的能量吸收原理，许多研究人员推导出了薄壁管在轴向载荷下的平均压溃力理论解。CHEN等[11]提出简化超折叠单元(simplified super folding element, SSFE)理论来预测单胞、双胞和三胞薄壁管的平均压溃力。基于SSFE理论，ZHANG等[12]从方形多胞薄壁管的截面中提取出角型、T形和十字形肋板结构，并推导出不同肋板结构的平均压溃力理论解。目前，典型肋板结构的平均压溃力的求解公式已广泛应用于多胞薄壁管平均压溃力的计算。QIU等[13]利用肋板结构理论模型[12]，推导出了4种不同截面六边形多胞薄壁管的平均压溃力理论解。YIN等[14]采用肋板结构的理论解来预测具有不同边数的多胞薄壁单管和双管的平均压溃力。根据上述研究可以发现，肋板结构的理论分析对预测薄壁管的平均压溃力是必不可少的。

在相关肋板结构理论研究的基础上，研究人员可设计出具有较优耐撞性的薄壁管。为突破传统薄壁管能量吸收效率的瓶颈，许多研究人员从仿生角度寻求突破。ZOU等[15]受到竹子内部微观结构的启发，设计了由仿竹结构组成的薄壁管，并论证了该薄壁管相对于传统薄壁管有更好的轴向和横向能量吸收特性；本课题组基于甲虫鞘翅微观结构，设计了一系列仿生多胞薄壁管，结果表明，仿生多胞薄壁管的耐撞性要优于传统多胞薄壁管的耐撞性[5]。仿生结构的加入使得仿生薄壁管相比于传统薄壁管在能量吸收方面更具有优势。目前关于肋板结构的理论解已有较为详细的研究，而有关仿生结构的理论研究报道相对较少。

综上所述，本文运用试验、仿真和理论分析方法对一种可构成薄壁管的仿生微圆结构(bionic microcircular structure, BMS)进行研究，并应用于汽车吸能盒结构设计。为验证有限元模型的可靠性和准确性，对BMS外接方管进行了准静态压溃试验。基于所建立的有限元模型对BMS结构和传统肋板结构(traditional rib structure, TRS)进行了参数化对比分析。基于SSFE理论，建立了BMS结构在准静态载荷下的平均压溃力理论解。

1 试验与仿真模型的建立

图1所示为成年甲虫的鞘翅微观结构[16]和提炼得到的仿生微圆结构(BMS)。通过观察甲虫的微观结构， 可以发现有许多空心圆柱管位于结构的交叉处。受到这种结构的启发，将类似的圆柱管添加到传统肋板结构(TRS)的连接处，进而得到BMS。

图1 甲虫鞘翅微观结构和提炼所得的BMSFig.1 Microstructures of beetle elytra and the BMS extracted from the microstructures

根据外接板数量N，将BMS分为3板仿生微圆结构(3-BMS)、4板仿生微圆结构(4-BMS)、5板仿生微圆结构(5-BMS)和6板仿生微圆结构(6-BMS)。图2对比了BMS与TRS的结构差异。

(a)N=3 (b)N=4 (c)N=5 (d)N=6图2 传统肋板结构与仿生微圆结构Fig.2 TRS and BMS

1.1 试验

为验证有限元模型的准确性，本文使用INSTRON 8802试验机对4-BMS外接方管进行准静态轴向压溃试验。试验样件见图3，样件的材料为铝合金AA6061-O。样件的材料参数设置如下：密度ρ=2.7×103kg/m3，弹性模量E=68.48 GPa，泊松比ν=0.3，幂率指数n=0.23。图4为从材料拉伸试验中获得的工程应力-应变曲线。压溃试验时将试样置于试验机的刚性顶板与底板之间，顶板以2 mm/min的恒定速度压溃试样，当压溃距离达到100 mm时停止移动顶板。

(a)整体 (b)横截面图3 试验样件Fig.3 Specimen used in test

图4 铝合金AA6061-O工程应力-应变曲线Fig.4 Engineering stress-strain curve of AA6061-O

1.2 有限元模型的建立与验证

根据压溃试验中试验样件的几何参数，建立了试验样件的有限元模型。本文采用Belyschko-Tsay四节点壳单元建模，壳单元沿厚度方向取5个积分点，单元网格尺寸为1 mm。本构模型采用分段线弹塑性模型，因铝合金为应变率非敏感材料，故在模型中忽略其应变率效应的影响。仿真中采用两种接触算法，一种是刚性墙与样件之间的点-面接触，另一种是样件本身的自接触[17]。各接触面的静态和动态摩擦因数均定义为0.2。

图5所示为试验样件在试验过程中4个时间点的变形以及仿真模型在同样时间点的变形，可以看出，有限元模拟的变形模式与试验的吻合度较高。将准静态压溃试验得到的力-位移曲线与有限元仿真得到的力-位移曲线进行对比，见图6，可以看出,仿真曲线与试验曲线具有相同的趋势。仿真和试验的压溃力峰值分别为38.12 kN和35.70 kN，平均压溃力分别为22.71 kN和21.85 kN。仿真与试验结果峰值力和平均力的误差分别为6.78%和3.94%。由此可知，有限元模型具有足够高的精度，可应用于后续研究。

(a)试验变形结果

(b)仿真变形结果图5 试验与仿真变形结果对比Fig.5 Comparison of deformed shapes obtained by test and simulation

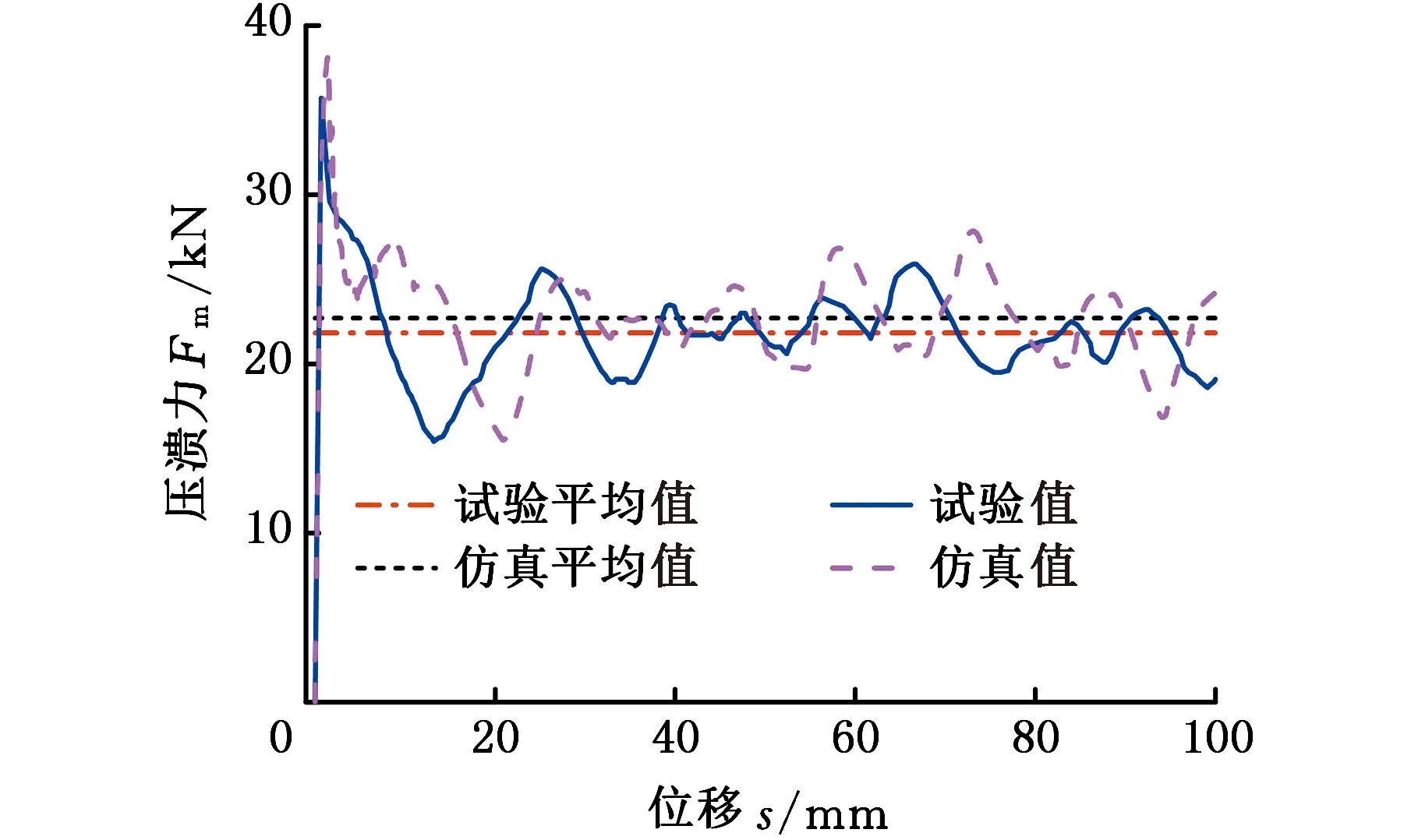
图6 试验与仿真的平均压溃力和力-位移曲线Fig.6 Mean crushing force and force-displacement curves obtained by test and simulation

2 仿真分析

在经过验证的有限元模型中，根据外接板数量N建立4组BMS模型和TRS模型，并对比它们的耐撞性表现。具体模型设置如下：每组模型中BMS和TRS的壁厚t分别取1.0 mm、1.2 mm、1.4 mm、1.6 mm和1.8 mm，且BMS中的圆柱管半径R分别取5 mm、6 mm、7 mm、8 mm和 9 mm。

为了评价BMS和TRS的耐撞性表现，将吸能量E、平均压溃力Fm和比吸能ESEA作为结构耐撞性评价准则。其中，吸能量E为结构在压溃过程中产生塑性变形所吸收的总能量，可由力-位移曲线积分得到，其表达式如下：

(1)

式中,d为结构的有效变形量;F(x)为瞬时冲击力。

在压溃过程中，平均压溃力Fm的计算表达式如下：

Fm=E/d

(2)

比吸能ESEA用来反映结构单位质量材料所吸收的能量，其表达式如下：

ESEA=E/m

(3)

式中，m为结构总质量。

由式(3)可知，ESEA越高，结构吸能效率越高，吸能效果越好。

为了对比BMS与TRS的能量吸收特性，将不同外接板数量的BMS与TRS的比吸能ESEA曲线绘制于图7中。由图7可以看出，BMS的ESEA曲线均高于TRS的ESEA曲线。以N=3时的曲线为例，当壁厚t=1.4 mm、3-BMS的中间圆柱半径R=5mm时，3-BMS的ESEA值比3-TRS的ESEA值大37.02%，此时为N=3时ESEA值的最小值；当N=3、t=1.6 mm、3-BMS的中间圆柱半径R=9 mm时，3-BMS的ESEA值比3-TRS的ESEA值大94.33%，此时为N=3时ESEA值的最大值。由此可知， 3-BMS的ESEA值相较于3-TRS的ESEA增长范围为37.02%～94.33%。同理，4-BMS的ESEA值相较于4-TRS的ESEA值增长范围为35.57%～57.94%，5-BMS的ESEA值相较于5-TRS的ESEA值增长范围为32.20%～56.42%，6-BMS的ESEA值相较于6-TRS的ESEA值增长范围为43.29%～63.31%。由上述研究结果可知，任何外接板数量N、结构壁厚t及BMS的中心圆柱半径R条件下，BMS的ESEA值始终大于TRS的ESEA值。这是因为中间圆柱的存在会使BMS在变形中耗散额外的能量。由图7还可以看出，随着结构壁厚t的增大，BMS的ESEA值呈明显的增大趋势。上述研究结果表明：BMS比TRS具有更好的能量吸收效率。

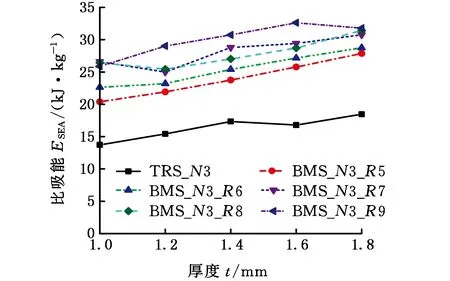
(a)N=3

(b)N=4

(c)N=5

(d)N=6图7 不同参数下TRS与BMS的比吸能曲线Fig.7 Specific energy absorption curves for TRS and BMS with different parameters

3 理论分析

3.1 理论模型的建立

BMS理论模型是基于简化超折叠单元(SSFE)理论[11]而建立的。SSFE理论假定压溃过程中形成的每个褶皱的波长(波长为2H)和壁厚均相同，因此，可以依据单个褶皱中的能量守恒来计算结构的平均压溃力。在实际压溃中，每个褶皱不可能被完全压实，因此，单个褶皱的有效压溃距离应为2Hk，其中k为有效压溃系数，这里取0.75[18]。依据能量守恒原理，压溃力Fm所做外功被结构以弯曲能Eb和薄膜能Em的形式耗散[11]，即

2HFmk=Eb+Em

(4)

为了分析BMS的平均压溃力，提取波长为2H的弧板单元(arc panel element，APE)为研究对象，弧板和外接板的长度分别为2ξ和L。BMS由APE组成，且APE的数量与BMS的外接板数量N相同。如图8所示，以4-BMS为例，4-BMS由4个APE组成。

(a)4-BMS(b)APE图8 仿生微圆结构与弧板单元Fig.8 Bionic microcircular structure and arc panel element

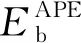
(5)

(6)

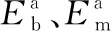
3.2 弧板单元的理论模型

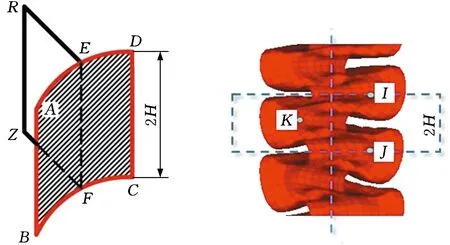
为研究弧板单元(APE)的理论解，可将APE分为弧板ABCD和外接板RZFE，见图9a。图9b为弧板ABCD的仿真变形图，图9c为弧板的塑性铰线和压缩延展单元。

基于SSFE理论，弯曲能由塑性铰线的长度和绕铰线弯曲的角度确定。从图9c中可以看出，塑性铰链线有3条：QP、AD和BC。在完全压溃时，QP的弯曲角为π，而AD和BC的弯曲角为π/2，因此，弧板耗散的弯曲能计算如下：

(7)

(a)弧板单元 (b)弧板仿真变形

(c)弧板塑性铰线与压缩延展单元图9 弧板单元中弧板变形模式与吸能Fig.9 The deformation mode and energy absorption of arc corner in APE

式中，M0为塑性弯矩；σ0为流动应力;σy为屈服应力;σu为极限应力;n0为幂率指数。

依据SSFE理论，弧板耗散的薄膜能可通过对塑性变形区域进行积分得到[11]。从图9c中可以看出，塑性变形区域由3个三角形EGI、KGH和HFJ组成。而图9c中三角形的面积由角度α决定，其中角度α为一个完整波长2H内弧板展开时塑性变形区域边界与弧板上下边界垂线的夹角，因此，弧板耗散的薄膜能计算如下：

(8)

式中，S为塑性变形区域面积；H为半波长。

对于图10a所示的APE中的外接板，图10b为其仿真变形，图10c为其塑性铰线和压缩延展单元。RE、ZF和WO为压溃过程中形成的塑性铰线，其旋转角分别为π/2、π/2和π，因此，外接板的弯曲能可表示为

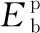
(9)

图10c中的阴影区域表示外接板中的延展单元，角度θ为外接板的垂线与圆弧板弦线的垂直线之间的夹角，见图10a。对塑性变形区域进行积分，可得到外接板耗散的薄膜能：

(10)

将式(7)和式(9)代入式(5)，可得到由APE耗散的总弯曲能：

(11)

同理，将式(8)和(10)代入式(6)，可得到由APE耗散的总薄膜能：

(12)

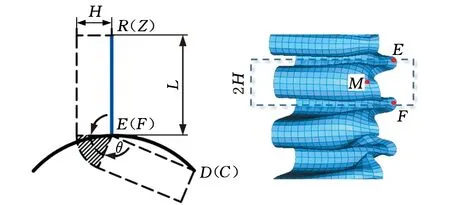
(a)弧板单元 (b)外接板仿真变形

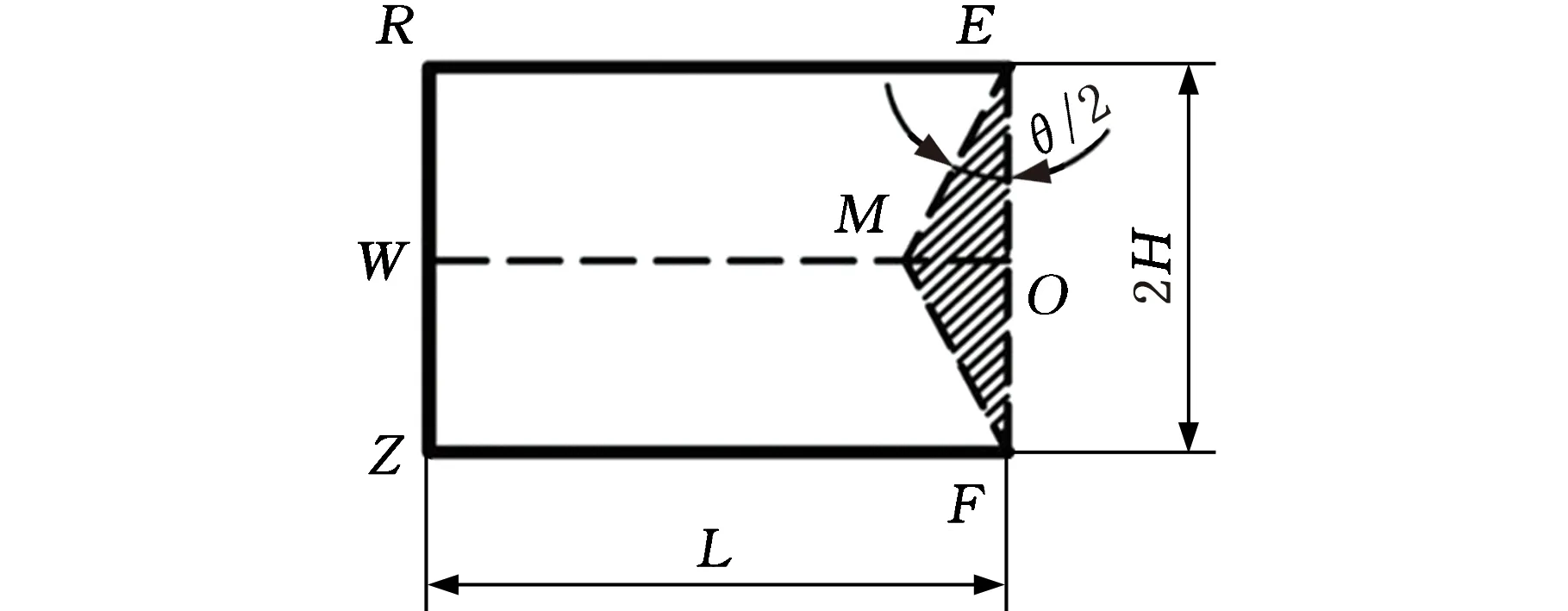
(c)外接板塑性铰线与压缩延展单元图10 弧板单元中外接板变形模式与吸能Fig.10 The deformation mode and energy absorption of additional panel in APE

3.3 仿生微圆结构的理论模型

在上述推导的基础上，可得出BMS的薄膜能耗散表达式：

(13)

BMS的弯曲能可通过计算每个褶皱中3个固定铰链线的能量耗散来确定，其表达式如下：

(14)

Lc=2πR+NL

式中，Lc为整个结构的截面周长。

将式(13)和式(14)代入式(4)，可以得到：

(15)

根据准静态条件[11]，有

(16)

根据式(15)和式(16)，可推导出H的表达式：

(17)

将式(17)代入式(15)，可得到Fm最终表达式：

(18)

定义

(19)

则式(18)可简化为

(20)

由式(20)可知：BMS的平均压溃力Fm随着材料塑性流动应力σ0、结构壁厚t、外接板数量N和截面周长Lc的增大而增大；与外接板数量N和截面周长Lc相比，结构壁厚t对BMS平均压溃力Fm的影响更大。

依据式(19)可以发现，系数λ的值由角度α和角度θ决定。当外接板数量N改变时，角度α与θ也会改变。为了得到系数λ的精确值，本文采用软件MATLAB进行式(20)的曲线拟合[19]，拟合数据点为有限元仿真结果。采用图7中BMS的Fm值对BMS平均压溃力公式进行拟合。根据不同的外接板数量N分为4组数据，每组共有25个拟合数据点，每个N对应不同的系数λ，结果列于表1中。其中，R2为拟合精度评价指标，R2值越接近于1，表明拟合精度越高。

表1 不同外接板数量对应的系数λ值

3.4 理论模型验证

为了验证BMS理论模型的准确性和实用性，对前文的试验结果进行验证。将该样件分成5个部分，包括4个3-TRS和1个4-BMS，如图11所示，样件在压溃过程中耗散的能量等于这5个部分耗散的能量总和。其中，b为3-TRS的边长，φ为3-TRS的夹角。

图11 试验样件横截面Fig.11 Cross section of specimen in test

由此可知，样件压溃过程中耗散的总能量可表示为

(21)

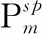
根据前文建立的BMS理论模型，4-BMS 耗散的能量包括薄膜能和弯曲能，可由式(13)和式(14)计算得到。其中N为4，λ=2.826(表1)，(tanα+2tan(θ/2))可通过式(19)计算得到，因此，可得到4-BMS耗散的总能量：

(22)

根据ZHANG等[10]的研究结果，3-TRS耗散的能量可表示为

(23)

式中，φ、L0分别为 3-TRS的角度和截面周长，这里φ为45°。

将式(22)和式(23)代入式(21)，可以得到

(24)

根据式(16)，可以得到半波长H的表达式为

(25)

将式(25)代入式(24)，可以得到试验样件的平均压溃力理论表达式为

(26)

试验中试样的壁厚t为1.2 mm。据前文所述，k取0.75。由式(26)计算得到的平均压溃力为23.95 kN。试验、仿真和理论得到的平均压溃力结果分别为21.85 kN、22.71 kN和23.95 kN，见图12。在3种方法得到的结果中，理论与仿真、理论与试验结果误差分别为5.46%和9.61%，误差均在可接受范围内(小于10%)，因此，BMS的理论解可为汽车吸能盒的耐撞性设计提供参考。

图12 试验、仿真与理论结果对比Fig.12 Comparison of the results obtained from test,simulation and theoretical analysis

4 结论

(1)与传统肋板结构相比，仿生微圆结构能量吸收效率的提升范围为32.20%～94.33%，其主要原因为中间圆柱的存在使得仿生微圆结构在变形过程中耗散额外的能量，进而提高了整体结构的能量耗散能力。

(2)建立了仿生微圆结构在准静态载荷下平均压溃力的理论表达式。该表达式表明仿生微圆结构的平均压溃力随着材料塑性流动应力、结构壁厚、外接板数量和截面周长的增大而增大；壁厚相对于外接板数量和截面周长对仿生微圆结构平均压溃力的影响更大。

(3)系数λ的值由角度α和角度θ决定，当外接板数量N改变时，角度α和θ会随之改变，因此仿生微圆结构的平均压溃力推导的系数λ值取决于N。通过曲线拟合得到系数λ的精确值后，理论表达式得到了试验数据的验证，可较好地预测仿生微圆结构的平均压溃力。