一类拟周期线性哈密顿系统的有效约化性

李 佳， 朱春鹏

(徐州工程学院数学与物理科学学院，江苏徐州221111)

假设A(t)是一个n×n矩阵，由Floquet定理知，如果A(t)是一个T周期矩阵，则x=A(t)x可以通过一个T周期变换，使其约化为常系数线性方程．Johnson等［1］进一步考虑了假设系数矩阵A(t)满足全谱条件，则拟周期系统x=A(t)x是可约化的．所谓的约化是指存在一个拟周期非奇异变换x=φ(t)y，其中φ(t)和φ(t)－1是拟周期且有界的，使得x=A(t)x变为y=By，其中B是常数矩阵．Jorba等［2］考虑了线性拟周期方程x=(A+εQ(t))x，其中x∈Rn，常数矩阵A是有不同的特征值．他们得到在非共振条件和非退化条件下，存在一个非空Cantor集E，使得当 ε∈E 时，方程是可约化的．Xu［3］把上面的结论推广到了有相同特征值的情况．Jorba等［4］考虑了非线性拟周期系统x=(A+εQ(t))x+εg(t)+h(x，t)，x∈Rn，其中 A有 n个不同的非零特征值．在非共振条件和非退化条件下，他们得到了ε∈E时，非线性系统是可约化的．Li等［5］进一步推广到了有重特征值的情况．但是，上面的文献只考虑了解析系统的约化性．近来，Li等［6］考虑了矩阵A不同特征值情况下，有限光滑拟周期系统x=(A+εQ(t))x的可约化性．虽然这样，上述文献的约化性都是约化到常系数矩阵的．不同于约化到常系数矩阵的情况，Jorba等［7］考虑了拟周期方程x=(A+εQ(t))x的有效约化性，其中常数矩阵A是有不同的特征值．他们得到在只有非共振条件，没有非退化条件的情况下，对于所有的参数ε，通过一个拟周期变换，系统可以约化为y=(A*(ε)+εR*(t，ε))y，其中R*关于ε是指数小的．最近，Li等［8］进一步推广到了有不同特征值的拟周期线性哈密顿系统的有效约化性．通过构造一个辛映射，使得这个有效约化保持了哈密顿结构．

受文献［7－8］的启发，本文把文献［8］的结果推广到有重特征值的情况．

定义 1 如果 f(t)=F(ω1t，ω2t，…，ωrt)，其中F(θ1，θ2，…，θr)对于所有变量都是 2π 周期的，且θi=ωit，i=1，2，…，r，则称函数 f是频率为 ω=(ω1，ω2，…，ωr)的拟周期函数．

如果 F(θ)，θ=(θ1，θ2，…，θr)在 Dρ={θ∈Cr‖Im θi|≤ρ，i=1，2，…，r}上解析，则称 f(t)在 Dρ上是解析拟周期的．记f(t)在Dρ上的最大值范数为‖f‖ρ=sup |F(θ)|．

θ∈Dρ

定义 2 如果所有的 qij(t)(i，j=1，2，…，n)在Dρ上是解析拟周期的，则称矩阵函数 Q(t)=(qij(t))1≤i，j≤n在 Dρ上是解析拟周期的．

1 主要结论

定理1 考虑哈密顿系统

假设 A=diag(λ1Ir1，λ2Ir2，……，λlIrl)，其中 Id是 d阶单位矩阵，r1+r2+…+rl=n，i≠j时，λi≠λj．假设 Q(t，ε)在 Dρ上是频率为 ω=(ω1，ω2，…，ωr)的解析拟周期矩阵，并且关于ε连续．假设下面的条件成立．

假设 1(非共振条件) λ=(λ1，λ2，…，λn)和ω=(ω1，ω2，…，ωr)满足

其中，k∈Zr{0}，τ＞r－1，α＞0 是一个小常数．

假设 2 记 Q(θ)=(Dij)1≤i，j≤l，其中 Dkk是 rk阶矩阵，1≤k≤l．定义 D=diag(D11，D22，…，Dll)．令［D］是D关于 t的平均．假设［Dii］的特征值为 δ1i，…，δrii，它们满足

其中，j≠j'，i=1，2，…，l，|ε|≤ε0，ζ是常数．

则对于所有的|ε|≤ε*≤ε0，存在一个拟周期辛变换 x=φ(t，ε)y，其中 φ(t，ε)在 Dρ上是频率为ω的解析拟周期矩阵，使得(1)式变为哈密顿系统

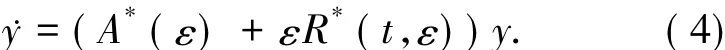
此外，有以下结论成立:

1)A*(ε)是常数矩阵，满足‖A*－A‖≤c1ε，其中c1＞0是常数;

2)R*(t，ε)在 Dρ上是频率为 ω=(ω1，ω2，…，ωr)的 解 析 拟 周 期 矩 阵，并 且 ‖R*‖ρ－δ≤是常数．

注 1 一般来说，Q(t，ε)依赖于 ε．下面为了简单起见，有时省略Q(t，ε)中的参数ε．

2 定理1的证明

事实上，本文重特征值的情况主要影响文献［8］的第一步 KAM迭代．因此，首先给出第一步KAM迭代，而以后的KAM迭代变为不同特征值的情况，完全类似于文献［8］．

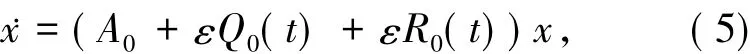
其中，A=A+ε［D］，Q=(Q－［D］)M，R=

000

(Q－［D］)≥M．类似于文献［8］，做辛变换 x=eεP0y，其中哈密顿矩阵P0将在下面定义，则方程(5)变为

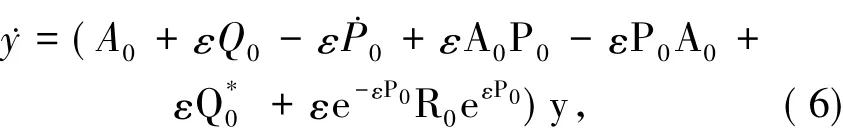
其中此时，希望系统(6)中Q0－P0+A0P0－P0A0=0，等价于解方程

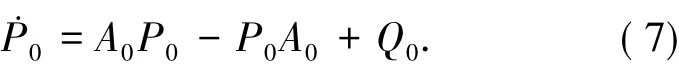
由假设2，即A0的特征值互不相同，于是，存在可逆矩阵 S，使得 珔A0=S－1A0S=diag(λ01，λ02，…，λ0n)，其中 A0的特征值为{λi+εδji}，i=1，2，…，l，j=1，2，…，ri．令S－1P0S=P珔0，S－1Q0S=Q珚0．于是，解方程(7)实际上变为解方程把P珔0和Q珚0展开为傅里叶级数 珚Q0=其中．如果并且当λ0i'和λ0j'分别是A0中不同的小分块矩阵的特征值时，|λ+i'－λ+j'|≥δ0，其中，M(ε)=?是常数，则通过比较

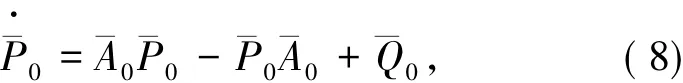
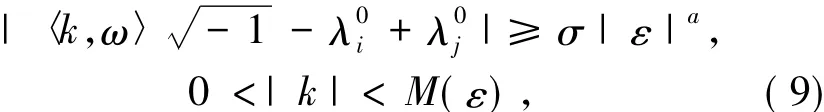
(8)式的傅里叶系数，有P珔0ij=0，(i，j)为矩阵 D 中小分块矩阵Dmm中的元素的坐标，1≤m≤l;其他，P珔kij=于是，方程(7)可解．另外，由于A0和Q0是哈密顿矩阵，于是P0也是哈密顿矩阵．具体证明见文献［8］中的引理2．2．此时，哈密顿系统(6)变为令Q0*=(D*ij)1≤i，j≤l，其中，D*kk是 rk阶矩阵，1≤k≤l．定义 D*0=diag(D*11，D*22，…，D*ll)．由于Q0*是哈密顿矩阵，于是D*0也是哈密顿矩阵．哈密顿系统(10)变为

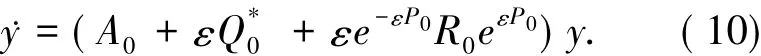
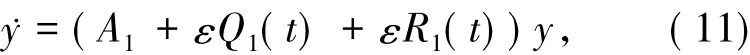
其中，A1=A0+ε［D0*］，Q珟0=Q*0－［D*0］，Q1=Q珟M0(ε)，

R1=Q珟≥0

M(ε)+e－εP0R0eεP0．A1、Q1、R1都为哈密顿矩阵．下面证明非共振条件(9)成立．当k∈Zr，0＜|k|时，由定理的假设1，有

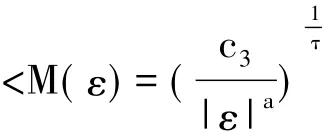
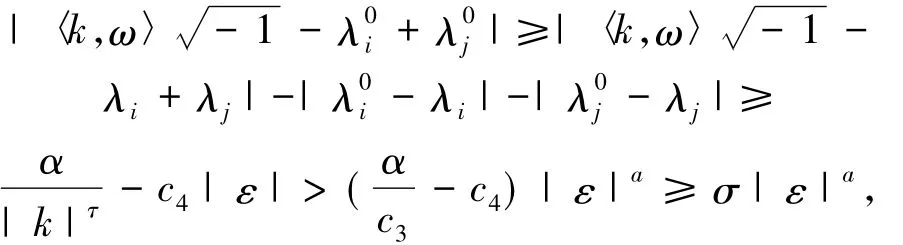
是常数．

对于哈密顿系统(11)，A1的特征值互不相同．这是因为，由文献［8］的(3．14)式，得到 Q*0=O(ε1－2a)，a∈(0，)．再由假设 2及(11)式，得到A1的特征值互不相同．事实上，对于下面每一步KAM迭代中的Ad，d∈Ν，它们分别都有不同的特征值．下面的证明完全类似于文献［8］，为了简单起见，此略．

致谢徐州工程学院科研项目(XKY2016214、XKY2016215和XKY2017113)对本文给予了资助，谨致谢意．