基于多尺度递归图理论的桥梁微弱信号非线性非平稳检验
张二华, 单德山, 李 乔
(1. 华东交通大学 土木建筑学院,南昌 330013; 2. 西南交通大学 土木工程学院桥梁工程系,成都 610031)
复杂运营环境下,发生微弱损伤的桥梁结构系统其本质是非线性、非平稳的,产生的动力测试信号为非线性、非平稳信号。由于桥梁所处的恶劣环境,这些幅度微小的信号又极易被强噪声所淹没。传统的频域信号处理方法均以傅里叶变换为基础,忽视了信号蕴藏的系统非线性非平稳信息;传统时域分析方法则常常直接提取有用信号的时域特征,抗噪性能很差[1]。而桥梁微弱动力测试信号的非线性、非平稳程度往往与初始损伤的发生和发展密切相关,这直接导致了基于传统信号处理方法的桥梁损伤识别结果无法满足工程的实际需求[2]。因此,研究强噪声环境下的桥梁微弱信号非线性、非平稳特征分析方法具有重要的实际意义。
针对信号非线性、非平稳特征分析,Eckmann等[3]提出了一种图形化的信号非线性、非平稳特征提取方法,即递归图(Recurrence Plot,RP)理论。在此基础上,Zbilut等[4]建立了递归量化分析(Recurrence Quantification Analysis,RQA)方法,构建了信号非线性、非平稳的量化指标。由于该方法摆脱了数据统计分布假设的限制,完全由信号驱动,且具有广泛的适用性,近年来已先后在生物医学工程、机械故障诊断、建筑结构损伤识别、风工程等领域[5-7]得到应用。
针对强噪声背景下的微弱信号非线性非平稳性检测,其最大挑战为消噪处理技术[8]。而基于滤波的常规方法在提高信号信噪比的同时,往往将部分有用信息一同滤除,造成原始信号的信息丢失。由Huang等[9]提出的经验模态分解(Empirical Mode Decomposition,EMD)从根本上摆脱了Fourier变换的局限性,非常适用于非线性、非平稳过程而受到广泛关注。马宏伟等[10]结合EMD和相关性分析,提出一种振动信号的降噪方法;吴杰等[11]提出了一种改进的交叉证认EMD小波滤波方法;范博楠等[12]对基于EMD的微弱声发射信号降噪方法进行了总结。
针对桥梁微弱信号的特点,将改进的集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法和递归图理论相结合,采用改进的EEMD方法将强噪声背景下的微弱信号分解为包含不同频带范围的信号分量,将递归图理论应用于不同信号分量,分析不同信号分量的递归特征,并引入RQA分析指标,对不同尺度的信号分量进行非线性、非平稳程度的定量描述,从而避免了直接从原始微弱测试信号提取准确的非线性非平稳特征的困难。
1 非线性非平稳分析方法
1.1 改进的EEMD方法
文献[13]针对桥梁动力测试信号的特点,提出一种改进的EEMD方法。其核心思想为:利用高斯白噪声的能量在全频域内均匀分布的特点,对高斯白噪声进行EMD分解,获得高斯白噪声各阶固有模态函数(Intrinsic Mode Function,IMF)分量,使用EEMD方法获得信号的第一阶IMF分量和分解余量,之后每次分解均是从原信号的分解余量开始,且每次仅取分解的第一阶固有模态,从而确保了模态分量的一致性,避免了EEMD中不同分解过程中模态分量不一致的问题。
改进的EEMD方法有效解决了桥梁结构动力测试信号噪声水平高、难以分离结构有效信号的问题,且该方法自适应水平高,本文将其用于桥梁微弱信号的自适应分解,以便为后续多尺度非线性非平稳性分析提供良好的信号分量。
1.2 递归图
递归图是一种N×N的二维图形,将相空间中的递归点以黑点表示、非递归点以白点表示,以达到表征信号系统动力学特征的目的。其基本理论阐述如下。
相空间重构是递归图分析的基础,对于长度为L的信号{x(1),x(2),…,x(L)},由时间延迟重构技术可得到延迟向量
X(n)=[x(n),x(n+τ),…,x(n+(m-1)τ)]T,
n=1,2,…,N
(1)
式中:X(n)为延迟向量;N为重构向量总个数,N=L-(m-1)×τ,m为嵌入维数,m可通过虚假邻近点法确定,τ为延迟时间,可通过互信息法确定。
递归图的数学模型表示为
Ri,j=Θ(ε-‖X(i)-X(j)‖),i,j=1,2,…,N
(2)
式中:Ri,j为递归值, 取0或1,i为行数,j为列数;ε为距离阈值; ‖·‖为欧式范数(Euclidean Norm);Θ(x)为海维塞函数(Heaviside Function), 当x<0,Θ(x)=0, 反之,Θ(x)=1。
距离阈值是一个经验值,它确定了一个以延迟向量X(i)为中心、ε为半径的领域。 当X(j)位于该领域内,Ri,j=1,否则Ri,j=0,最后,即可将一个N×N的状态距离矩阵转换为0~1的递归矩阵,以二维图形表示出,即为递归图。
1.3 递归量化分析
递归量化分析指标均是建立在递归点密度、递归图对角线和垂直线基础之上。递归图的对角线反映了信号状态的复杂性,能够揭示信号状态分叉的发生和混沌的程度,以递归图对角线长度为基础的RQA指标可作为信号非线性特征的定量指标;递归图竖直线反映了信号状态无变化或变化极为缓慢的时间步,以递归图竖直线长度为基础的RQA指标可作为信号非平稳特征的定量指标。
1.3.1 非线性测度
测度熵ENTR(entropy)是递归图中平行于主对角线的长度为l的对角线长度分布的Shannon熵,测度熵反映了递归图中对角线分布的复杂程度,是一个对系统复杂度变化非常敏感的测度。
(3)
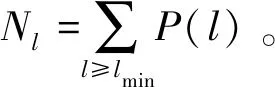
1.3.2 非平稳测度
垂直线平均长度,常称为捕获时间(Trapping Time,TT)代表了系统维持在某一状态不发生转变的平均时间,即TT越小,代表系统某一状态保持不变的时间越短,TT越大,代表系统维持某一状态不变的时间越长,该测度可有效反映系统的非平稳程度。
(4)
基于上述理论和方法,提出一种强噪声背景下信号非线性非平稳特征多尺度分析方法,简述如下:首先,将原始信号s(n)进行改进的EEMD分解,获得各阶IMF分量,计算各阶IMF分量与s(n)的相关性系数,去除趋势项;然后重构其余IMF的相空间,构造每一个IMF的递归图;最后,基于各阶IMF的递归图,对各阶IMF进行RQA分析,获得各阶IMF的非线性非平稳测度。
2 模拟信号测试
2.1 模拟信号和整体递归量化分析
构造典型非线性非平稳Rössler信号,叠加噪声水平约为100%的随机噪声,如图1所示。Rössler信号数学模型为

(5)
式中:x(0)=y(0)=z(0)=0.1;a=0.2;b=0.2;c=5.7; 采样时间间隔Δt=0.2 s。
由虚假邻近法和互信息法,计算了信号图1(c)的延迟时间τ和嵌入维数m,重构了其相空间。基于相空间,建立了整体信号的状态距离矩阵,绘制了状态距离云图。根据Zbilut等和Marwan等的研究结论,ε取信号相空间最大半径的10%,建立了整体信号的递归图,如图 2所示。由图2可知,整体信号的相空间分布发散,状态距离矩阵及递归图呈现递归点均匀分布的特征,非常接近随机白噪声的信号模式特征;递归量化指标值如表1所示,ENTR值和TT值均较小,上述现象表明强噪声已严重污染了信号的递归特征,基于强噪声背景下的微弱信号整体递归分析,严重失真。
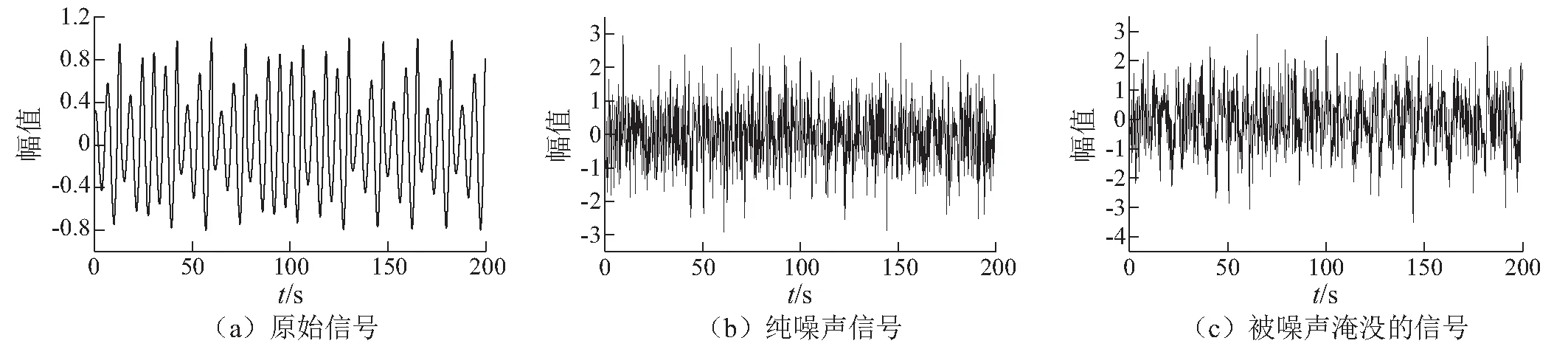
图1 模拟信号Fig.1 Simulated signals
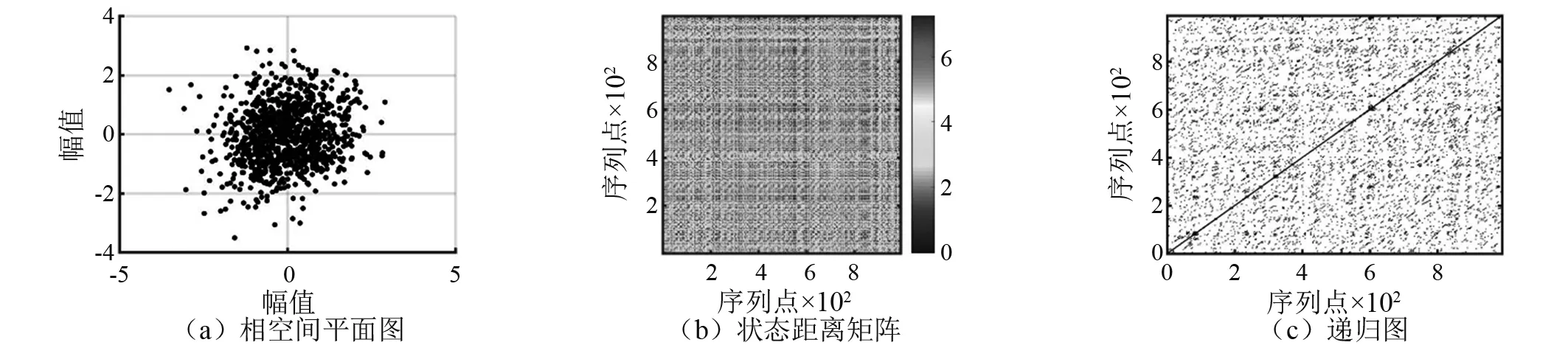
图2 强噪声背景下微弱信号整体递归分析流程图Fig.2 Flow chart of global recursive analysis for weak signals in strong noise environment
2.2 自适应分解及多尺度递归量化分析
采用改进的EEMD方法,对被噪声淹没的信号进行分解,获得各阶IMF如图3所示。
分别计算各阶IMF与原始信号的相关性系数,其中IMF8~IMF11分量的相关性系数小于0.05,可认为相关性极为微弱,作为趋势项进行了剔除。
2.3 多尺度递归图及递归量化分析
与整体信号相空间重构采用的方法相同,分别计算了IMF1~IMF7的延迟时间τ和嵌入维数m,重构了IMF1~IMF7的相空间。基于相空间,分别建立了IMF1~IMF7的状态距离矩阵,绘制了无阈值递归图(即状态距离二维图)。与整体信号递归图阈值的选取方法一致,ε取各IMF相空间最大半径的10%,建立各IMF的递归图,如图4~图6所示。

图3 原信号的各阶IMF分量Fig.3 Each IMF component of the original signal
由图4~图6可知:①IMF1的相空间图均匀分布,无吸引子;IMF2~IMF4的相空间图相对不规则,存在突变和吸引子;IMF5~IMF7的相空间图相对规则,无明显吸引子;②IM1的递归图孤立点均匀分布,无对角线、竖直和水平方向的线段,表现为典型均匀模式,线性、平稳特征显著;IMF2~IMF7的递归图出现显著的带状白色条纹,竖向线结构明显,表现为典型的非平稳过程,其中竖向和水平向带状白色条纹越多,表示信号状态分层越剧烈,其非平稳性越强;③IMF2~IMF5的递归图出现对角线方向的线段,线段走向大体平行于45°主对角线方向,且对角线和孤立递归点并存;IMF6~IMF7对角线分布更加复杂,孤立递归点逐渐减少,对角线走向表现为弧形特征,表现为漂移模式和突变模式的组合,其非线性程度增强。
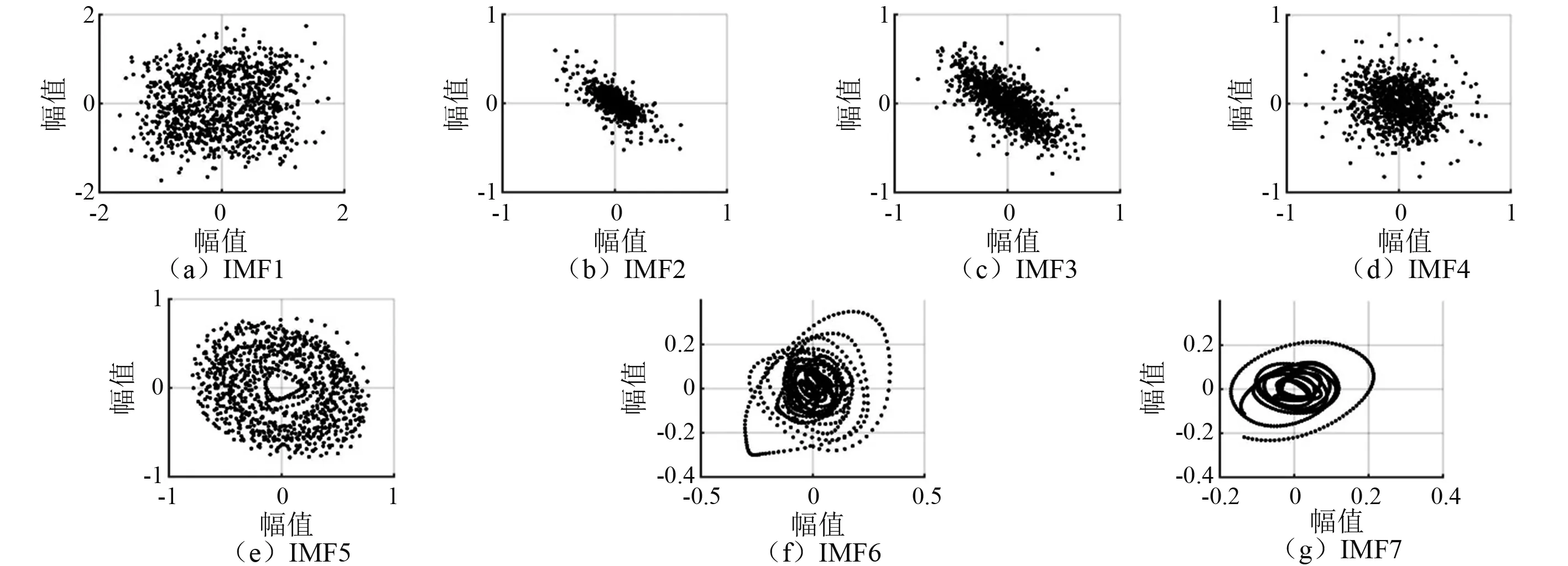
图4 IMF1~IMF7的相空间模式特征Fig.4 Pattern features of IMF1—IMF7’s phase space

图5 IMF1~IMF7的状态距离矩阵模式特征Fig.5 Pattern features of IMF1—IMF7’s state distance matrix
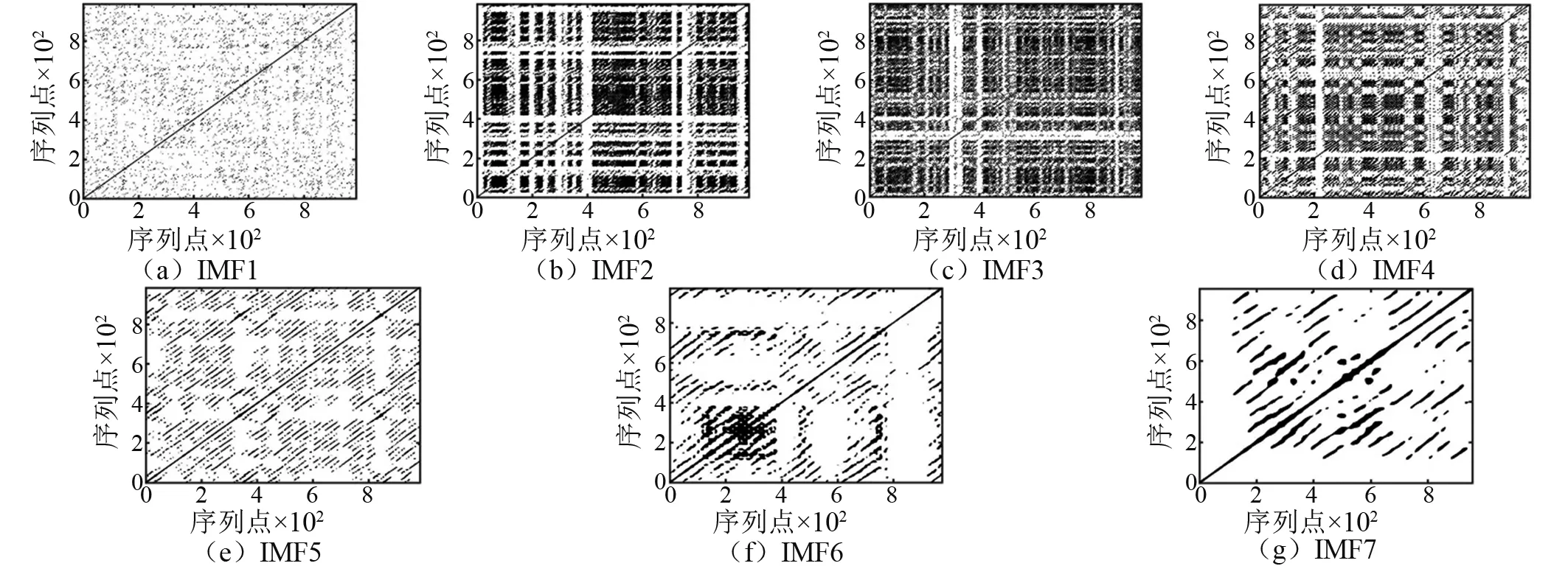
图6 IMF1~IMF7的递归图模式特征Fig.6 Pattern features of IMF1—IMF7’s recurrence plots
通过RQA分析,获得了各阶IMF的非线性非平稳测度值,如表1所示。由表1可以得出:①对于非平稳测度值,IMF1的TT值为0,表明信号为典型随机过程;IMF6和IMF7的TT值较大,表明信号状态滞留的平均时间较长;IMF2~IMF5的TT值较小,信号状态滞留时间较短,非平稳程度强于IMF6~IMF7;②对于非线性测度值,IMF1的ENTR值为0,表明信号为典型线性过程;IMF6~IMF7的ENTR值大于IMF2~IMF5,信号的复杂度较高,非线性程度强于IMF2~IMF5;③各IMF的非线性非平稳测度值能准确的反映递归图中的模式特征信息。
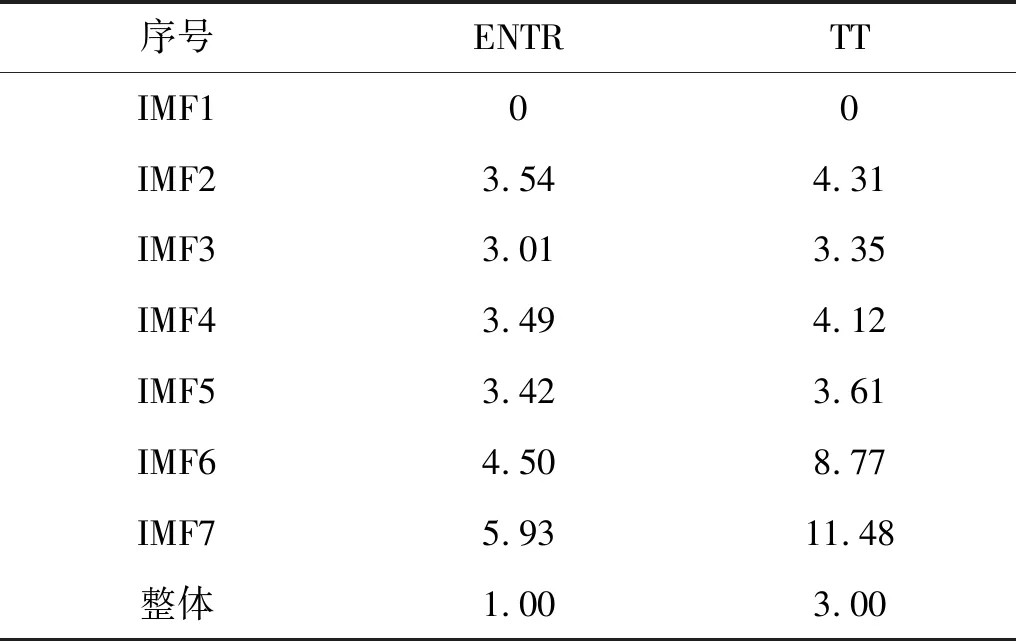
表1 整体及多尺度非线性非平稳测度值
3 桥梁实测信号应用
采用某主跨1 088 m斜拉桥的桥塔加速度测试数据对本文方法进行检验与应用。实桥传感器布置概况可参见文献[14]。信号采样频率为20 Hz,截取测试时间为100 s。选取的加速度信号如图 7所示。
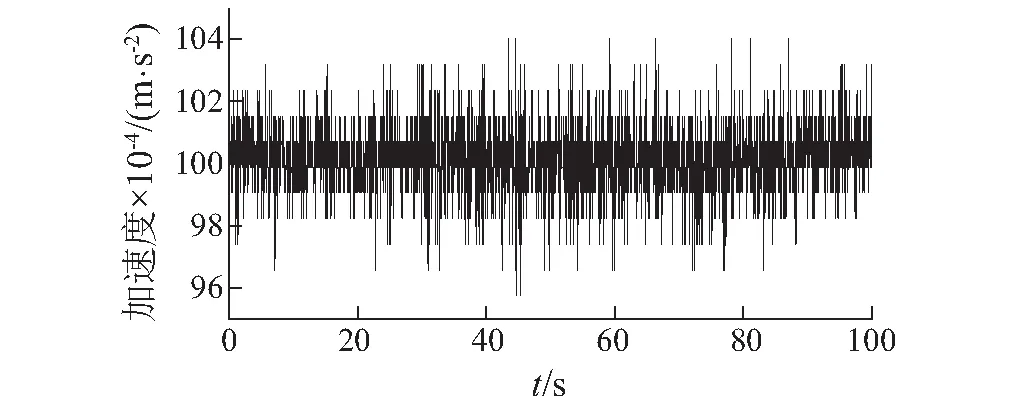
图7 桥塔实测加速度测试数据Fig.7 Real acceleration test data of bridge tower
采用改进的EEMD方法对实桥进行自适应分解,获得各阶IMF,并计算各阶IMF与原信号相关性系数,去除相关性微弱的趋势项分量,最后剩余IMF1~IMF8分量,其过程与模拟信号的分解与剔除趋势项过程类似。
与模拟信号测试过程相同,分别计算了整体信号的递归图及各阶IMF的递归图,并进行递归量化分析。如图8~图9所示。
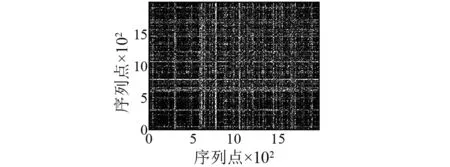
图8 整体信号的递归图Fig.8 The recurrence plot of the whole signal
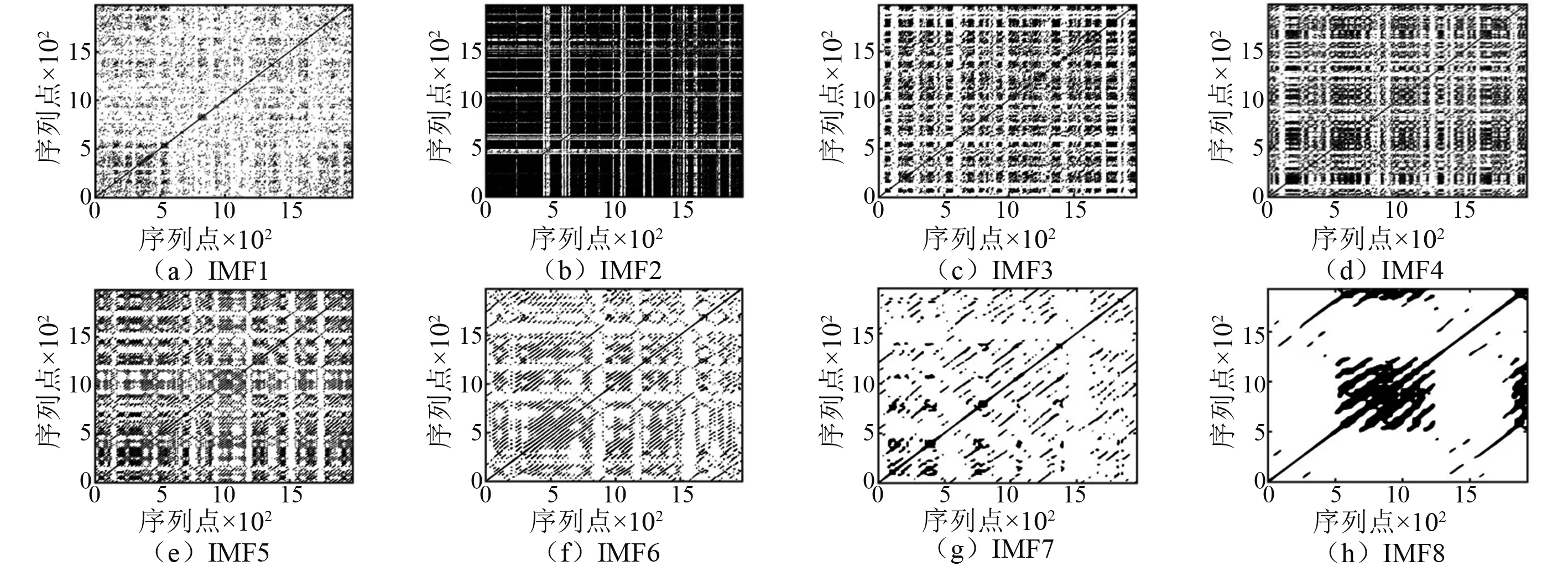
图9 各阶IMF的递归图模式特征Fig.9 Recurrence plots pattern features of each IMF
与模拟信号类似,由图8~图9可知:①对于恶劣测试环境下的实桥动力测试信号,直接采用递归量化分析,其递归图中蕴藏的递归拓扑结构受到随机噪声的严重污染,已无法准确获得信号真实的非线性非平稳特征;②将恶劣测试环境下的实桥动力测试信号进行自适应分解后,其各IMF分量的递归图模式特征存在明显差异,递归拓扑结构清晰可辨。
由RQA分析,获得整体信号和各阶IMF的非线性非平稳测度值,如表2所示。
由表2可知,类似模拟信号RQA分析结果,各IMF的非线性非平稳测度能够较准确的量化不同递归图模式的特征信息;进一步表明,本文所提方法,能准确获得恶劣测试环境下实桥动力测试信号不同尺度的非线性非平稳特征,较直接采用递归分析法,所提取的信息物理意义明确,信息更加丰富。

表2 整体及多尺度非线性非平稳测度值
4 结 论
经模拟信号测试与实桥动力测试数据的检验与应用,可得如下结论:
(1) 对于强噪声背景下的桥梁微弱信号,直接采用整体递归量化分析方法提取信号非线性非平稳特征,其递归图不能有效揭示信号的递归拓扑结构,分析结果精度较差。
(2) 基于多尺度的递归量化分析能够较好的揭示强噪声背景下微弱信号各成分的非线性非平稳特征,提取的递归图清晰可辨,选取的递归量化分析指标对递归图包含的非线性非平稳信息敏感。
(3) 本文所提方法能有效提取实桥恶劣测试环境下的动力信号不同尺度非线性非平稳特征,提取的信息丰富准确;由恶劣测试环境下实桥分析结果表明,本文所提方法能用于实桥测试信号的非线性非平稳特征检验中。

