一种多阈值融合心音递归图的设计与应用

成谢锋， 汪 晶， 王 悦

(1. 南京邮电大学 电子科学与工程学院，南京 210003；2. 江苏省射频集成与微组装工程实验室，南京 210003)

心音信号是人体重要的生理信号之一，它包含了关于心脏各个部分如心房、心室、心血管以及各个瓣膜功能状态的生理信息，具有普遍性、稳定性、独特性和可采集性等生物特征[1]。课题组在心音信号的基础上构建了心血管健康评估系统(进入了研究生电子设计大赛全国总决赛并获奖)-“生命心衣”，为了达到快而高效的效果，本文从二维的角度对心音部分进行分析。

心音信号是典型的非线性信号，并且具有混沌特性，而递归图是分析时间序列周期性、混沌性的一种重要的非线性分析方法[2]。但在利用递归图进行分析时存在两个关键性难题：第一，递归图适合对较短数据的处理，一旦数据太长，就会明显增加数据的处理时间，心音是准周期性信号，一般对心音信号的分析至少是2～3个周期，甚至更长,因此，必须对心音信号进行前期处理；第二，递归图对阈值参数的要求很高，如果阈值选择过小，递归图中将几乎没有递归点，也难以提供有用的递归结构特征；若阈值选择过大，某些递归结构特征将会被掩盖，从而出现错误的递归特征。对于递归图阈值的选择，很多学者进行了相关的研究工作[3-5]，但这些方法对于心音特征的表征不一定有效，因此，寻找一种适用于心音信号分析的阈值至关重要。

为了解决上述存在的两个难点，本文提出了相应的解决方法。首先，为了解决数据长度的问题，前期需要对心音信号进行等分等长处理，既选出心音信号所在频段,又保留了心音信号适当的数据长度,并得到用于递归图处理的等分等长心音系数。其次，针对递归图阈值的选取问题，本文提出了一种自适应阈值的获取方法，并且考虑到心音信号的复杂性，通过单个阈值获取的递归图在表征心音信号的特征时将出现困难,因此，在自适应阈值的基础上构建了一种多阈值融合心音递归图，这种心音递归图能最佳的表现心音特征。通过从多阈值融合心音递归图中提取D′2/S′2值和灰度共生矩(Gray-Level Co-occurrence-Matrix, GLCM)的4种特征：能量、对比度、相关性和熵，并将这些特征作为支持向量机(Support Vector Machine, SVM)的输入进行分析。

1 分析的前提

图1中，Ⅰ为正常心音的波形； 波形中的T1为第一心音S1的持续时间；T2为第二心音S2的持续时间；T12为S1～S2的持续时间；T21为S2～S1的持续时间。Ⅱ为Ⅰ对应的递归图。为了明确两者之间的关系，并考虑到Ⅰ和Ⅱ的横坐标点数不一致，因此，将Ⅱ中纵横坐标扩展成与Ⅰ的横坐标长度一致，然后将Ⅱ中横坐标方向上的矩形图块左右边界线与Ⅰ对照分析,并用直线标记，逆时针旋转90°，即得到Ⅲ。结合Ⅲ，并对Ⅰ和Ⅱ中的图形同时从左至右进行对比，Ⅰ中第一次S1持续的时间与Ⅱ中第一次出现矩形图块左侧的空白间隔相等，Ⅰ中第一次S1～S2的持续时间与Ⅱ中第一次出现矩形图块的宽度相等，Ⅰ中第一次S2持续的时间与Ⅱ中第一次出现矩形图块右侧的空白间隔相等，Ⅰ中第一次S2～S1的持续时间与Ⅱ中第二次出现矩形图块的宽度相等。以此类推，这种关系表现在Ⅲ中，即从上往下的直线依次对应Ⅱ中从上至下矩形图块的左右边界线。当只考虑Ⅱ中对角方向上的情况时，可以得到Ⅳ中的对角化图形。将Ⅰ与Ⅳ进行对比可知，Ⅳ小方块的边长T12′与Ⅰ中的T12相等，Ⅳ大方块的边长T21′与Ⅰ中的T21相等，因此对于时域波形上T12/T12可以通过递归图中T12′×T12′/T21′×T21′得到， 时域上S1/S2可以通过Ⅳ中T12′/T21′得到。由于一维波形上T12/T12和S1/S2在二维递归图上得到了放大，因此利用递归图对心音进行分析是可行的。

图1 心音与递归图的关系Fig.1 The relationship between heart sound and recurrence plot

在一个心动周期内，可以分为收缩期(systolic,S)和舒张期(diastolic,D)两部分，其中收缩期持续时间为S1的开始到S2开始前， 舒张期持续时间为S2的开始到下一个心动周期S1开始前， 将T1，T2，T12，T21与心音的收缩期和舒张期联系起来，可以得到S=T1+T12，D=T2+T21， 为了便于后续分析令S″=T12,D″=T21。

因此，本文设计的一种多阈值融合心音递归图和分类识别方法的原理图，如图2所示。

图2 系统框架图Fig.2 The frame diagram of system

2 分析方法

2.1 获取等分等长心音系数

利用RP对心音信号进行处理时存在的第一个关键难题，即：RP适合对较短数据的处理，数据过长会明显增加数据的处理时间，如何降低数据的长度。

定义1对信号s(t),通过某种变换降低数据的长度,获取信号所在的频段，消除其它频段杂音,称为等分处理;再对所选信号进行多层等长度分析,凸显信号的时频细节特征, 称为等长处理;这种既保留原始信号s(t)的所有特征信息同时又降低信号长度的方法，称为等分等长处理。

设对信号s(t)等分p段，ε(t)为单位阶跃信号,bk(k=1,2,…,p)为等分处理系数，则经过等分处理后，任意一段信号可表示为

(1)

任意选择等分处理后的一段信号进行等长处理, 得到q个等长信号，则等长处理后的任意一个信号可表示为

ski(t)=aisk(t)i=1,2,…,q

(2)

式中：ai为等长处理系数。

定义2设Hc(t)是时序心音信号经过等分等长处理得到的，在保留原始心音信号的所有特征信息的同时降低了心音信号的长度，则Hc(t)称为等分等长心音系数。

等分等长心音系数Hc(t)具有如下特性：

(1)Hc(t)不仅保留了心音信号的周期性，能量集中性，相对稳定性等特征，并且频段为心音信号的主要频段范围，凸显了心音的时频特征；

(2)Hc(t)的数据长度相对于原始心音信号的长度明显降低了，同时又避免了心音信号长度过短的情况，很好地满足了递归图的处理要求。

等分等长心音系数Hc(t)获取步骤：

步骤1任意选择待分析心音信号中4～6 s长度的信号；

步骤2为了获取心音信号所在的频段，采用心音小波对原始心音信号进行m层小波分解，使得第m层的频带低于500 Hz, 并令第m层的低频信号为Hl(t), 高频信号为Hh(t)；

步骤3为了凸显心音的时频特征，对等分处理后的Hl(t)进行d层小波包分解， 得到u=2d个信号， 即Hl1(t)，Hl2(t)，…，Hlu(t)， 选择经过等分等长处理后所有长度一致的， 得到2k+1 个信号，即等分等长心音系数Hc(t)。

2.2 多阈值融合心音递归图的获取方法

利用RP对心音信号进行处理时存在的第二个关键难题，即：RP对阈值参数的要求很高，阈值的设置直接影响RP对心音信号内部结构的呈现情况,如何选择合适的阈值。

2.2.1 一种自适应阈值θ的获取方法

设{x1,x2,x3,…,xn}为时序心音信号， 嵌入维数为m， 延时时间为τ， 则相空间重构后的矩阵为

(3)

令N=n-(m-1)τ，对相空间矩阵任意两列之间求距离，得到距离矩阵为

(4)

距离矩阵反映了在相空间中，每一个向量在相空间的位置状态与其他向量之间的距离变化情况，因此从距离矩阵出发选择合适的阈值更具有合理性。令Yi={di1,di2,…,dii,…,diN}， 其中i=1,2,…,N，为了反映距离矩阵D中每一个向量Yi的统计分布，对其求均值，即为

(5)

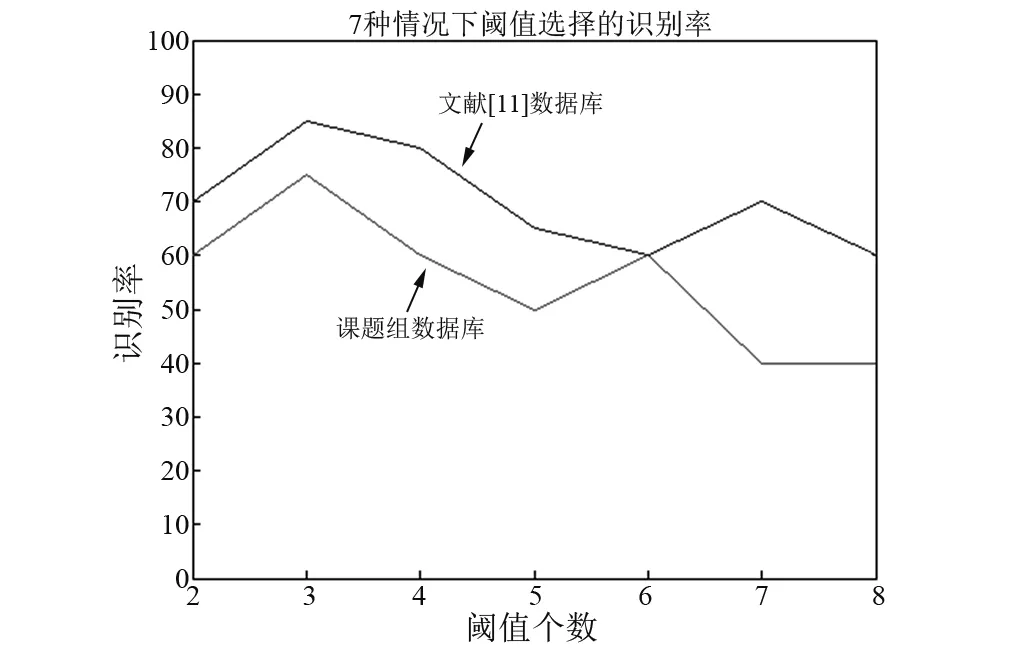
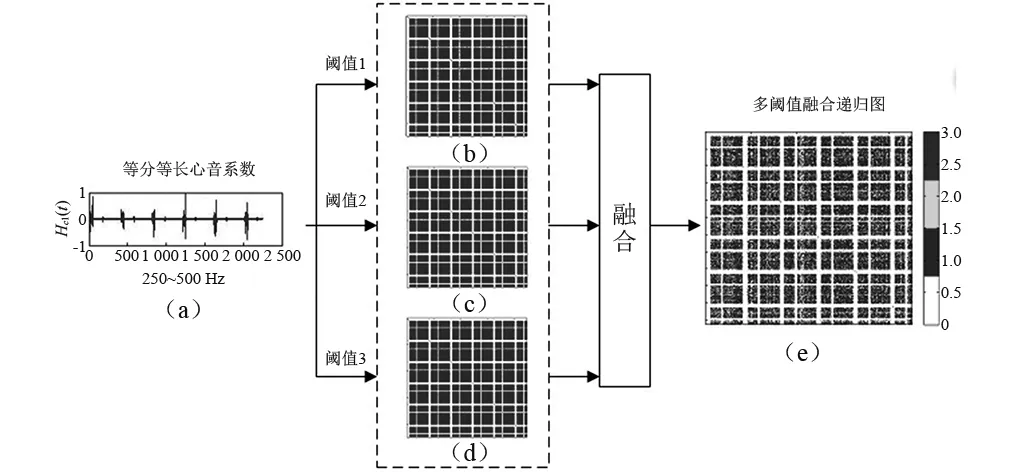
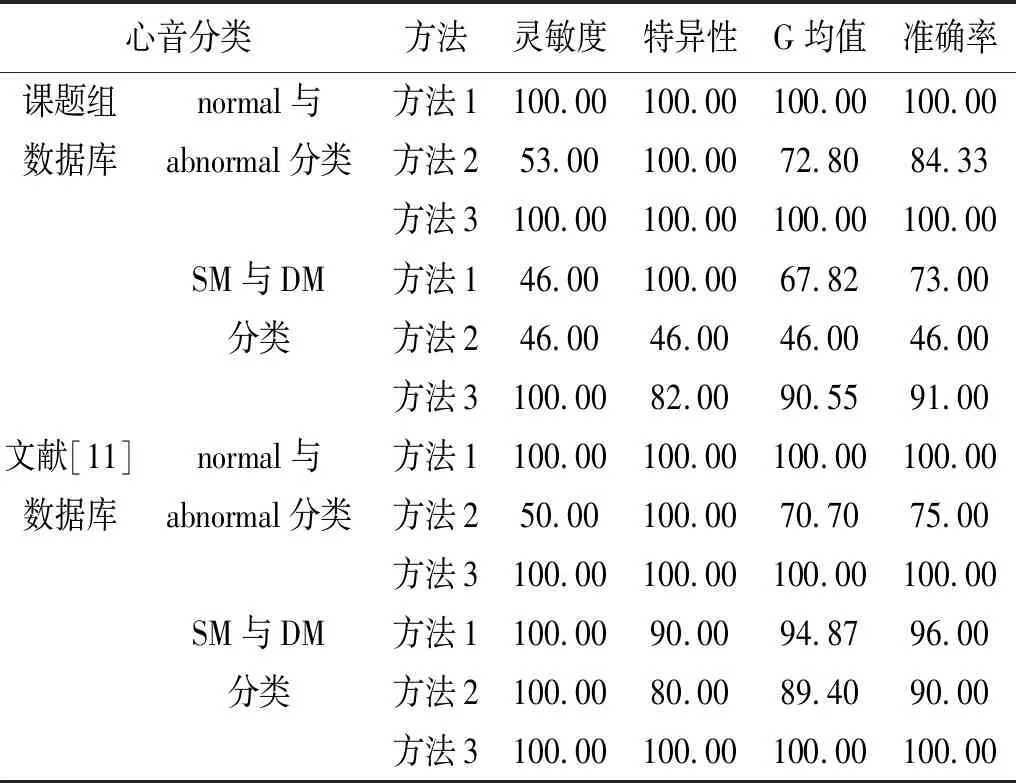
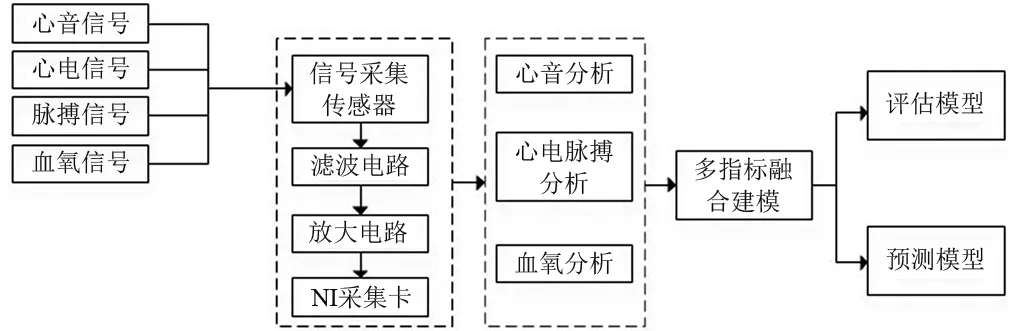
对距离矩阵中每一个向量Yi进行均值分析后， 得到了均值向量，即:E={E1,E2,…,Ei,…,EN}T。 为了便于数据分析，只保留小数点后四位，同时去掉均值向量E中重复的元素，可得到变换后的互异均值向量，即Et={E1,E2,…,Ei,…,Ep}T,p

θ=Ei|max(W)

(6)

2.2.2 基于自适应阈值θ的多阈值融合心音递归图

本文提出的阈值选择方法是选取权重最大的元素对应的均值，当权重最大的元素出现重复现象时，阈值选择将会出现困难。因此，本文在自适应阈值的基础上提出了一种多阈值融合心音递归图。

定义3设R为等分等长心音系数经过多个阈值处理得到的递归矩阵的融合，则称之为多阈值融合递归矩阵。

为了便于对多个阈值的分析，将Et改写为Et1={E1,E2,…,Ei,…,Ep}T，W改写为Wt1={w1,w2,…,wi,…,wp}。首先进行阈值分类，选择Wt1中最大元素在Et1中对应的值作为第一类阈值e1f={ε11,ε12,ε13,…,ε1f}，其中f

选取不同个数的阈值进行融合处理得到的多阈值融合递归图在表征心音特征上是不同的。灰度共生矩阵的灰度级数一般取8级或16级[7]，考虑到运算效率，因此，本文选择了前8个阈值进行分析，并按照只选择前两个，只选择前三个,只选择前4个，只选择前5个，只选择前6个，只选择前7个，只选择前8个，即7种情况进行分析。对数据库中的心音采用这7种情况进行多阈值融合处理，依次对得到的多阈值融合心音递归图提取D′2/S′2值和灰度共生矩特征，并按照十折交叉验证[8]的方法对文中两个数据库的normal和abnormal情况进行分析，结果如图3所示。

图3 7种阈值选择方法的识别率分析Fig.3 The recognition rate analysis of seven threshold selection methods

根据文献[9]中的互信息法和Cao算法计算得到嵌入维数和延时时间参数，设定为m=3，τ=1，同时选择三个阈值进行多阈值融合处理。图4为对一例正常心音进行等分等长处理后得到的其中一个等分等长心音系数Hc1(t)进行多阈值递归图融合的分析。

图4 等分等长心音系数的递归图融合原理图Fig.4 The schematic diagram of recurrence plot fusion on equal part and equal length heart sound coefficient

图4(a)为归一化心音经过等分等长处理后得到的等分等长心音系数Hc1(t)； 图4(b)为阈值为e1f时， 对应的递归图R1；图4(c)为阈值为e2v时，对应的递归图R2； 图4(d)为阈值为e3z时，对应的递归图R3； 图4(e)为三个阈值得到的递归图进行融合后的多阈值融合递归图。从图4(e)中可以看出，经过多阈值处理得到的多阈值融合递归图不仅保留了心音特征T1，T2，S″和D″，同时S″和D″的长度更加精确了。

2.3 特征提取

2.3.1 提取多阈值融合心音递归图的D′2/S′2值

将得到的多阈值融合心音递归图进行对角化处理，则D′2/S′2值的获取步骤为：

步骤1由于采集的心音信号不都是周期的整数倍，得到的S″和D″的个数不都相等，首先统计多阈值融合心音递归图中S″和D″的个数，若两者相等不做舍去操作，若两者不等，舍弃较多的个数，使两者保持相等；

步骤2考虑到心音是非平稳准周期信号，随机选择其中一个S″和D″会造成较大的误差性，因此，分别对步骤1中的S″和D″进行求和处理，得到S′=ΣS″，D′=ΣD″；

步骤4分别对S′和D′进行平方处理，得到S′2和D′2，并获取最终的特征值value=D′2/S′2。

2.3.2 提取多阈值融合心音递归图的GCLM

为了获取多阈值融合心音递归图中不同灰度级之间的空间相关性，采用灰度共生矩阵提取纹理特征。Haralick等定义了14种描述灰度共生矩阵[10]的特征参数，本文选取最常用的4种提取多阈值融合心音递归图的纹理特征。

(1) 二阶矩

(7)

(2) 对比度

(8)

(3) 相关性

(9)

式中：μ1，μ2，σ1，σ2分别为均值和标准差。

(4) 熵

(10)

通过对式(4)的分析可知，距离矩阵是关于斜率为-1的对角线对称的，即得到的递归图是关于135°角对称的，因此在计算灰度共生矩阵时，只用考虑0°，45°，135°三个方向的纹理特征。

3 数据分析

3.1 数据来源

文中的数据库来源于课题组心音数据库和文献[11]中的心音数据库，由于递归图可以将D/S值放大，因此将两个数据库中的异常心音分为收缩期杂音(Systolic Murmur, SM)和舒张期杂音(Diastolic Murmur, DM)。由于数据的来源不同，使用的采样频率有差异，为了便于数据分析，统一将心音信号转换成采样频率为2 000 Hz的形式。

3.2 结果分析

3.2.1 不同阈值选择方法的对比分析

为了验证本文提出的自适应阈值获取方法的有效性，分别与文献[12]中标准差的10%，文献[13]中标准差的15%，文献[14]中标准差的25%和文献[15]中标准差的5倍4种阈值选择方法进行对比分析。并采用十折交叉验证方法对normal与abnormal的分类以及SM与DM的分类进行分析，结果如表1所示。

从表1可以看出，对于文中的两个数据库，不管是对正常心音与异常心音的分类，还是对收缩期杂音与舒张期杂音的分类，本文提出的方法较其他4种方法识别效果更好，即本文提出的阈值设置方法是有效的。

表1 5种阈值选择方法的识别率对比分析

3.2.2 不同递归图选取方法的对比分析

为了验证本文提出的多阈值融合心音递归图的可行性，选择3种方法获取递归图，方法1选择一个阈值获取递归图；方法2选择三个阈值获取递归图，不进行递归图融合处理；方法3将三个阈值的递归图进行融合处理。同样地，采用十折交叉验证方法对normal与abnormal的分类以及SM与DM的分类进行分析，并采用文献[16]中的评价指标，最终的结果如表2所示。

表2 识别结果

从表2可以看出，采用多阈值融合递归图不仅可以有效地实现正常心音与病理心音的分类,还能较好地实现异常心音的分类。其中文献[11]中数据库的整体识别效果比课题组数据库的整体识别效果更好，原因在于文献[11]中的心音信号比较干净，几乎没有背景噪声。

3.2.3 不同算法的对比分析

为了进一步验证本文提出方法的有效性，利用3种算法与本文提出的算法进行对比分析，并按照十折交叉验证方法对normal和abnormal情况进行分析，结果如表3所示。从表中数据可知，本文的识别效果较好，即本文的分析方法是有效的。

4 算法应用

课题组自主设计了心血管健康评估系统-“生命心衣”，其中包括心音传感器，心电传感器，脉搏传感器，血氧传感器。首先利用自主设计的传感器实现4路信号的实时采集，并对采集后的信号利用LABVIEW平台进行前期预处理，包括数据存储和心音信号的时频分析，然后对采集的数据进行心音，心电，脉搏，血氧分析，通过提取它们各自的特征参数构建心血管评估指标，最后利用得到的多个指标构建心血管评估模型和预测模型。系统框架图如图5所示。

图5 生命心衣系统框图Fig.5 The system diagram of life heart clothing

通过采用本文所述方法对采集的心音信号提取特征，能够有效减少多路信号之间的影响，并且不用对心音信号进行分段处理，就能实现心音的正常与异常分类，提高了计算的实时性，并与同步采集的心电、脉搏、血氧信息一起，在线分析人体血糖(GLU)，平均动脉压(PM)、心率(HR)、心脏搏血量(SV)、脉搏波传导时间(PPT)、脉搏传导速度(PWV)等多个生理参数，通过对这些生理参数数据的融合处理，构建心血管评估模型，并通过对测试者长期测试数据的分析，构建预测模型，可预估测试者未来心血管健康的发展趋势。

5 结 论

针对课题组构建的心血管健康评估系统中对心音的分析，采用本文提出的分析方法，可以得到有效地评估效果。因此，本文设计的一种多阈值融合心音递归图，并提取其D′2/S′2值和灰度共生矩特征进行分类识别为心音的分析提供了一种新途径。

(1) 采用等分等长处理方法进行前期处理，避免了对S1，S2进行分段操作，同时获取的等分等长心音系数，很好地满足了递归图的处理要求，也是获取较高识别率的基础。

(2) 递归图对阈值的要求较高，本文设计自适应阈值的获取方法，简单且容易获取，并且相对于其他阈值选择方法，识别效果提高了10%～30%。

(3) 多阈值心音递归图的最佳阈值个数为3，相对于其他阈值个数，识别效果最好，并且将三个阈值得到的递归图进行融合，信号的内部结构得到了有效地呈现，递归图的纹理特征更加丰富。

(4) 通过提取多阈值融合递归图的D′2/S′2值和灰度共生矩特征参数，识别效果可以达到90%～100%，并且在相同条件下，相对于其他特征提取算法，识别率提高了5%～15%。