基于响应面与灵敏度分析的区间不确定性参数识别方法

陈学前， 沈展鹏， 刘信恩

(1. 中国工程物理研究院 总体工程研究所，四川 绵阳 621999;2. 工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621999)

可靠的动力学模型对于结构的动力响应预测和结构动态设计都具有十分重要的意义。因此，常常需要根据结构振动或模态试验结果对结构的有限元模型进行修正，使有限元分析结果能更好服务结构的工程设计。为此，有限元建模与修正技术在过去30多年取得了长足的发展[1-6]，但当前绝大多数的模型修正方法都属于确定性方法，没有考虑结构参数和响应的不确定性，大大降低了其工程实际的应用价值。然而，由于工程问题普遍存在不确定性，如结构材料参数与几何尺寸的不确定性，结构在服役期间的各类装配带来的装配不确定性，试验测试数据的不确定性等，迫切需要开展考虑不确定性的结构动力学有限元模型修正方法研究。考虑不确定性的有限元模型修正可以分为概率模型修正和区间模型修正两大类。在概率模型修正方面，最初的概率模型修正是采用统计方法仅考虑噪声引起的试验结果随机性的问题[7]，也有研究者将贝叶斯方法应用于模型修正以获得更加可靠的识别结果[8-9]，近年来，为提高模型修正效率，有学者结合摄动法与灵敏度分析方法开展了不确定性模型修正[10-13]。但概率修正方法的精度依赖于对结构参数和响应概率分布特性的准确估计，这类方法需要大量的试验数据以建立准确的概率分布函数，增大了工程应用的难度。相比较，采用区间分析的不确定性有限元模型修正对试验数据没有严格要求，为此，当前许多学者提出了区间响应面模型以及模型修正的区间反演方法[14-16]。但是，由于区间数运算法则和传统数学算法非常不同，采用区间分析方法，待修正参数的区间在迭代的过程中容易发散，在数值计算方面存在困难。目前常见的办法是将区间模型修正问题转化为确定性修正过程，如基于区间响应面模型，利用响应上下限构造目标函数并按照区间序数关系，将不确定性优化目标和约束条件转化为确定性表达式，从而避免区间数运算可能导致的优化困难[17]。此外，也有学者提出将区间分析与灵敏度分析结合起来修正区间参数的中值与区间宽度[18]，但当参数初始区间估计不合理时，二者同时进行修正可能降低优化效率，并且可能使修正结果与实际结果出现偏差。

本文考虑试验模态数据以及结构参数的区间不确定性，将不确定性模型修正分成两步独立的优化过程，基于灵敏度分析与响应面模型，完成了结构中区间不确定性参数进行识别。最后，通过两个算例对所提出的方法进行了验证。

1 试验样本区间的中值与半径分析

考虑结构某些参数为区间不确定性时的动力学模型修正，首先需要确定关心试验结果的区间不确定性，但是，结构动力学试验所获取的响应样本量通常是小样本，其样本数一般在几个～十几个。为此，在进行模型修正前需要对小样本试验结果的区间进行准确估计，以得到可靠性的修正模型。

针对小样本数据的区间边界估计，常用的方法有Bootstrap法、核密度估计法、模糊范数法和灰自助法。有研究表明，变窗宽的核密度估计方法估计得到小样本数据的区间边界更可靠[19]，因此，本文采用变窗宽的核密度估计方法来估计试验结果的区间边界，以获得变量区间中值与半径。

核密度估计作为一种非参数估计方法，是区间边界估计的一种重要方法。它并不提前假定总体分布的形式，而是以核函数(如三角形窗、高斯窗、指数窗等)为权重，用待估计点x邻域内其他样本的值作为该点的估计值，其估计函数如式(1)所示。

(1)

式中：K为核函数；h为窗宽

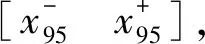
(2a)

(2b)

2 不确定性参数识别方法

本文基本思想是将不确定性参数识别方法分为两步实施：第一步利用传统确定性有限元模型修正与参数识别方法，并结合响应面代理模型修正得到待修正参数的中值；第二步基于代理模型，采用灵敏度分析方法分析得到待修正参数的半径，结合第一步修正结果，完成结构中区间参数的识别。

2.1 区间参数的中值优化识别

该问题属于结构确定性参数识别方法，传统的各种确定性模型修正方法(如神经网络法、遗传算法、响应面法等)均可使用。考虑到响应面法由于具有计算量小，精度较高，且待修正参数与响应量之间具有显示函数关系，便于后续进一步开展基于灵敏度分析的不确定性参数区间宽度修正，本文采用多项式响应面函数作为代理模型，开展结构系统的不确定性有限元模型修正与参数识别。

响应面法的基本思想是假设随机输入变量对结构响应变量的影响可用数学函数来表达，通过确定性有限元方法在随机输入变量空间构造有限样本点，用二次多项式拟合这些样本点，得到响应面函数。

研究表明，参数间相互效应对响应面模型总方差的贡献非常小[20]，故本文采用无交叉项的二次多项式模型，其表达式为

(3)

式中:b0,bi及bii为待定系数，需根据试验样本点的计算结果对其进行识别。

基于多元线性回归的多项式响应面需数据样本，针对实际工程中因素较多的情况，常用的试验设计方法有中心复合设计法(又称CCD(Central Composite Design)法)和Box-Behnken矩阵设计法(又称BBM(Box-Behnken Method)法)。本文采用试验设计方法为BBM法，该方法的设计点由设计参数的中心点和边界点组成。

通常响应面的精度依据可根据式(4)判断

(4)

传统确定性的有限元模型修正可归结为如下优化问题

(5)

由于待修正参数的初始区间可能估计不准，或对于高度非线性模型，由于待修正参数的初始设计空间较大，拟合精度难以保证，参数识别可能陷入局部最优，因此，借鉴文献[21]自适应响应面方法解决该问题，即待修正参数的中值修正可能需要进行多步确定性的修正过程。设定优化收敛的判据|Fk+1-Fk|/Fk≤ε1或Fk≤ε2，若不满足，则以最近获得的参数优化值为中心，缩放或平移新的参数关心区域，重新取得试验设计点，并对结构开展相应的动力学计算分析、响应面构建及优化分析。结构待修正参数的中值修正流程图，如图1所示。

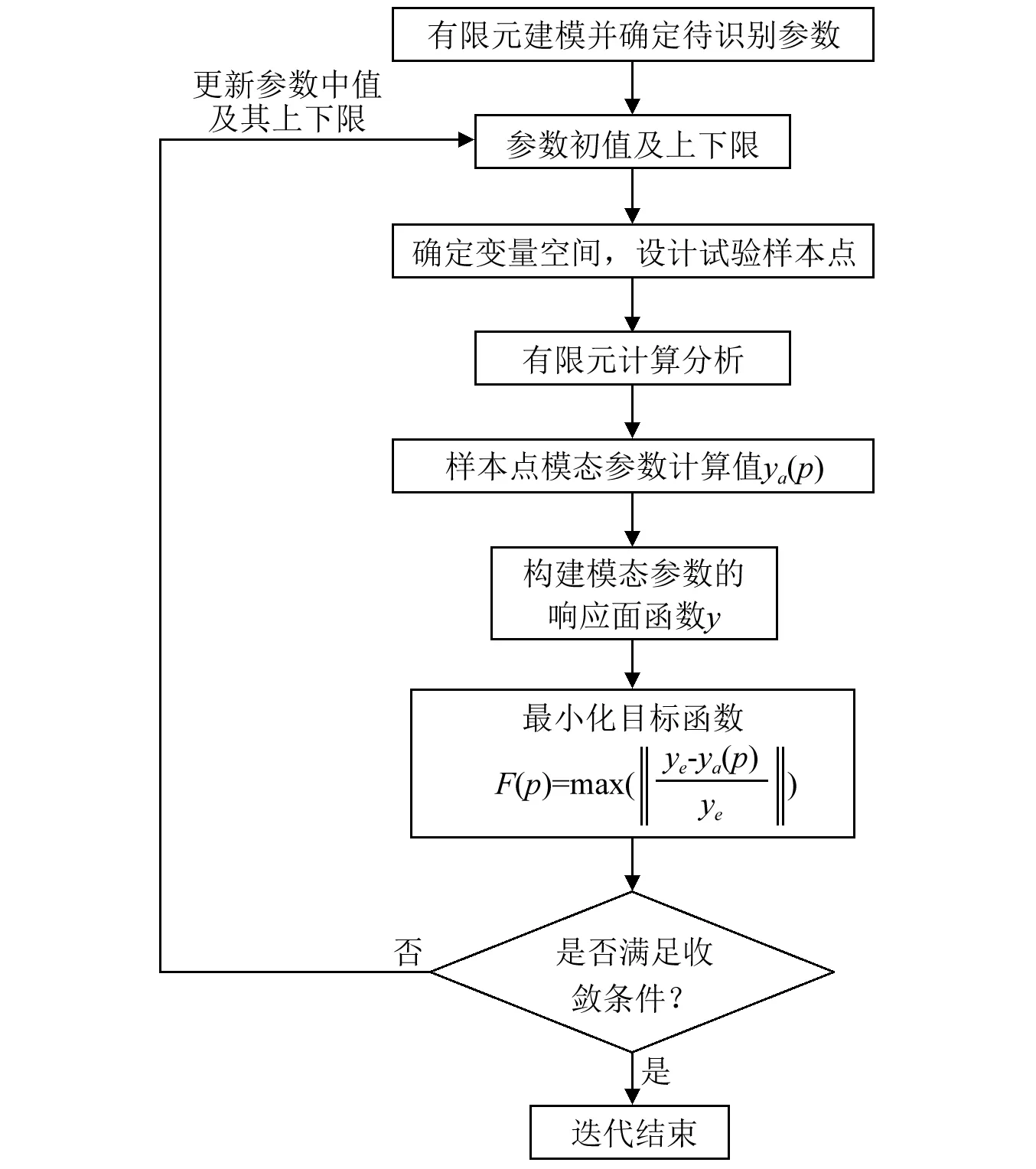
图1 基于响应面的区间参数中值识别流程图Fig.1 Flow chart identifying the mean of uncertain parameters

2.2 区间参数的半径优化识别

假设待修正参数p是具有不确定性的结构参数，用区间方法可以将其描述为

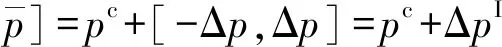
(6)

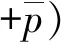
对于具有区间参数p的结构，其特征值λ(p)也具有区间性质，由于特征值在前章节通过二次响应面模型近似，则将其在区间中值附近进行Taylor展开，有

λ(p)=λ(pc+Δp)=

(7)

采用区间数学中的区间自然扩张理论，根据式(7)，通过区间运算，可得特征值区间的上、下界及区间不确定性分别为

(8a)

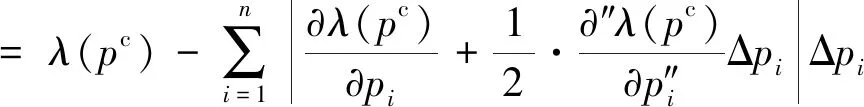
(8b)

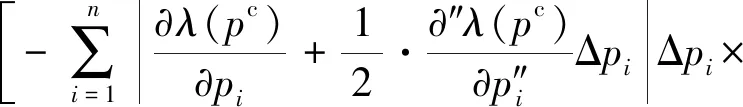
(8c)

采用灵敏度分析的方法迭代求解优化问题，有限元模型修正问题描述为

ye-ya_ j=Sj(pj+1-pj)

(9)

式中：Sj=∂ya_ j/∂pj为待修正参数关于模态参数的灵敏度矩阵；可以根据响应面模型式(3)方便计算得到。

考虑到试验数据与结构参数的区间不确定性，将式(9)中的变量采用区间方法表示为

(10)

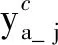
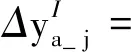
(11)

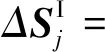
(12)

将式(10)代入式(9)，可得

(13)

为了识别得到待修正参数的区间半径，采用摄动法，将式(13)中关于Δ的零阶项和一阶项分离，并忽略二阶项的影响，得到

(14)

求解式(14)，得到待修正参数区间半径的迭代表达式为

(15)

根据上述分析，得到待修正参数的区间半径优化识别过程，如图2所示。

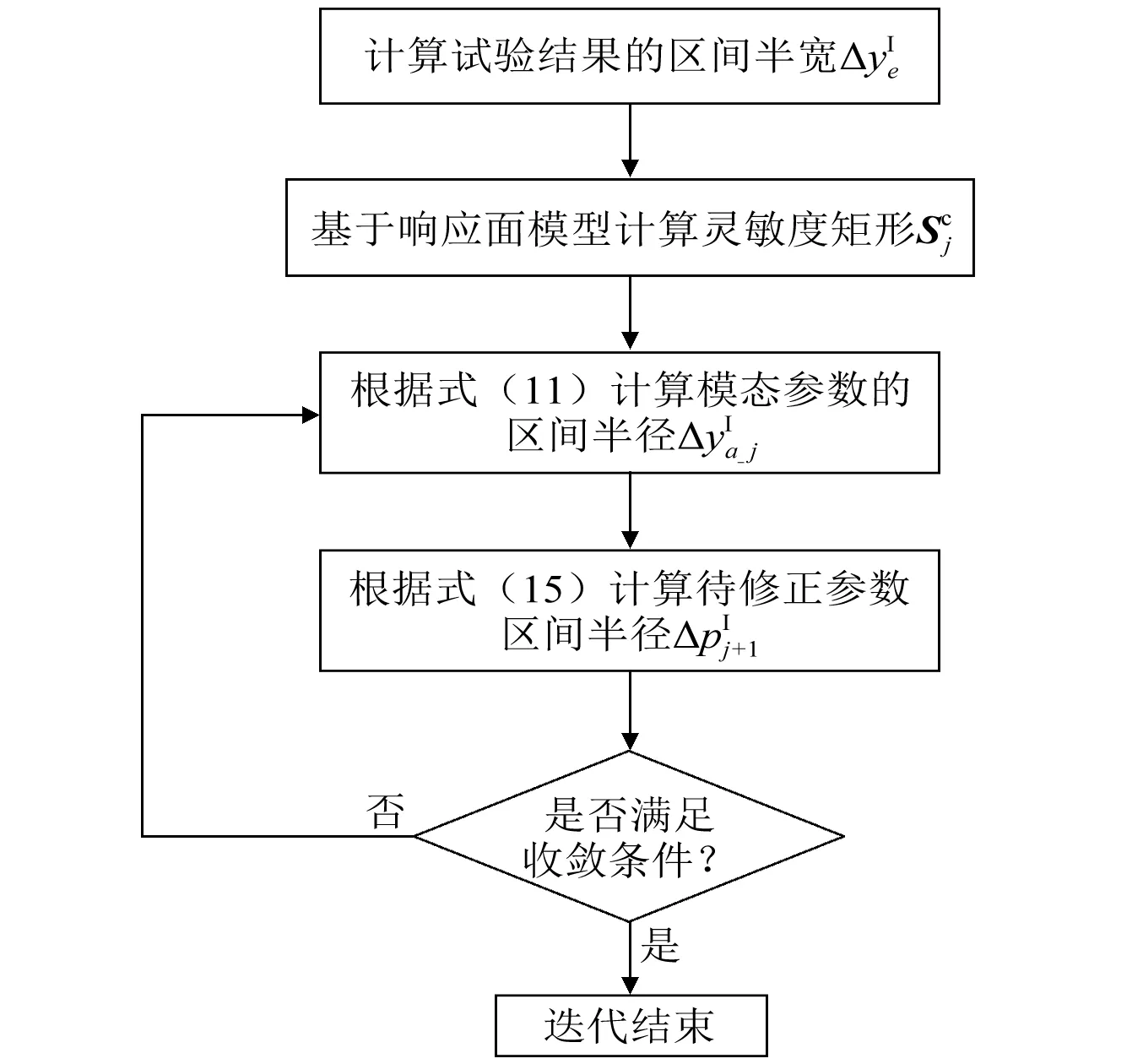
图2 不确定性参数区间半径识别流程图Fig.2 Flow chart identifying the radius of uncertain parameters

3 算例研究

3.1 两自由度系统的参数识别

如图3所示两自由度系统，模型中确定性的参数有m1=m2=1 kg，k1=1 N/m。模型中不确定性参数取值区间为k2=[0.8,1.2] N/m，k3=[0.9,1.1] N/m。

图3 两自由度质量—弹簧系统Fig.3 Two degree of freedom mass-spring system

假定不确定性参数为均匀分布，采用拉丁超立方抽样方法构造20个试验样本，计算得到系统的前两阶固有频率样本，并采用非参数核密度估计法估计试验样本的95%置信区间，根据式(2a)、式(2b)计算得到频率f1,f2试验结果的样本中值分别是0.999 3 rad·s-1和1.731 3 rad·s-1，区间半径分别是0.033 2 rad·s-1和0.157 0 rad·s-1。

假定k2,k3的初始区间值都为[1.5,2.5] N/m。根据图1所示区间参数中值优化流程，开展其中值识别，经过5步迭代即收敛，且每个迭代步中所建立的响应面模型的R2>0.999，k2，k3中值的迭代收敛情况如图4所示。优化识别得到k2,k3的中值分别为0.999 5 N/m和0.997 3 N/m。

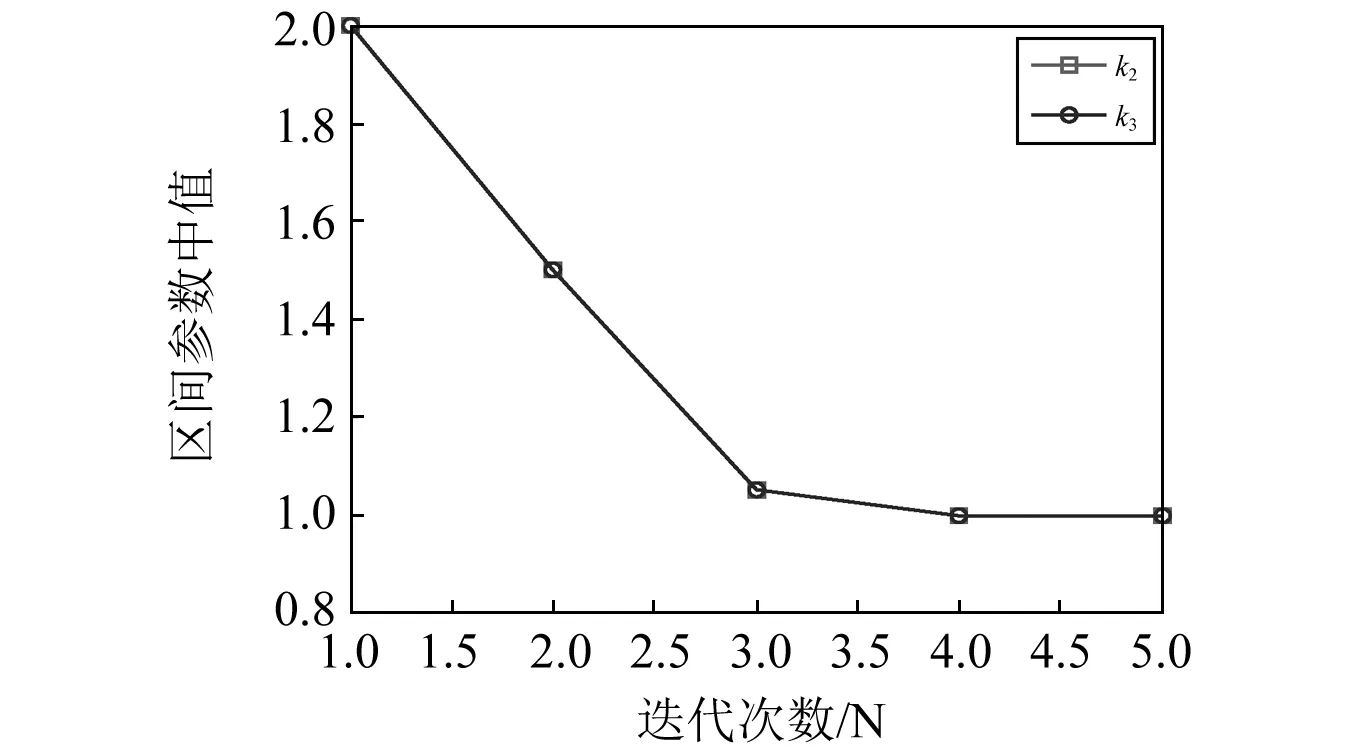
图4 区间参数中值迭代收敛情况Fig.4 Convergence curves of the means of uncertain parameters

根据图2所示参数区间半径优化流程，通过3步迭代即收敛，k2,k3半径的迭代收敛情况如图5所示。优化识别得到k2,k3的区间半径分别是0.239 6 N/m和0.127 6 N/m。

图6为修正前后不确定性参数区间的比较。根据待修正参数修正前后的区间值，采用均匀分布的拉丁超立方抽样方法构造1 000个随机样本，并计算系统的前两阶固有频率，并与试验数据进行比较，散点图如图7所示。

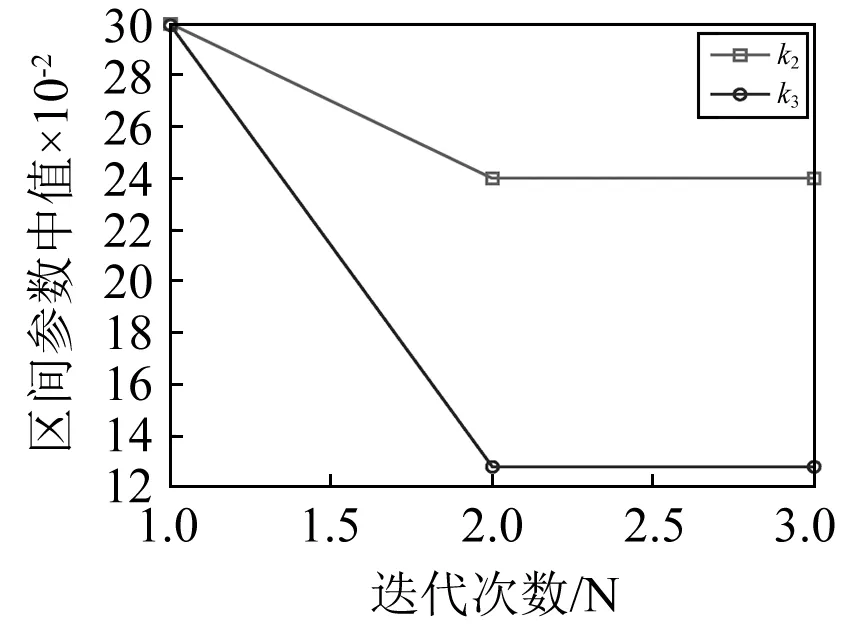
图5 区间参数半径迭代收敛情况Fig.5 Convergence curves of the radiuses of uncertain parameters

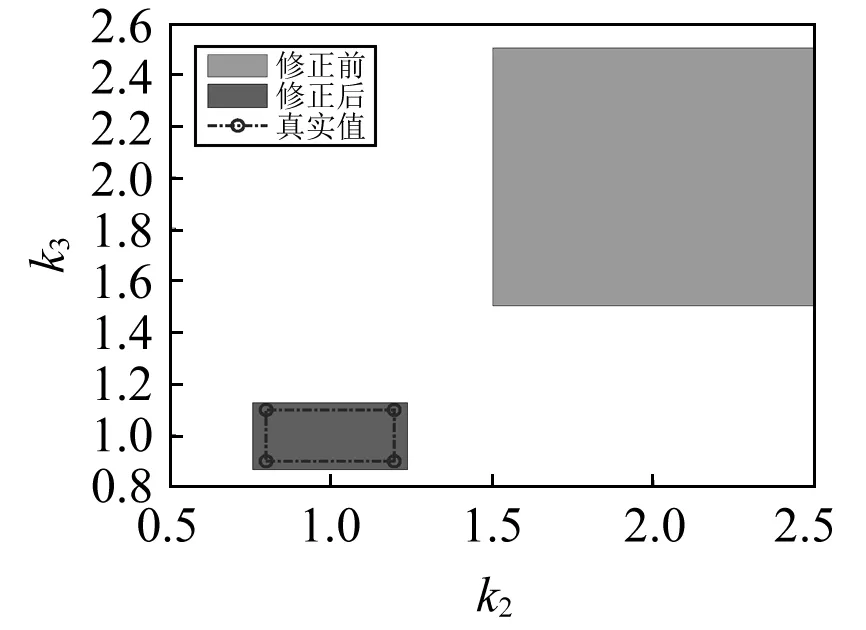
图6 修正前后区间参数的比较Fig.6 Comparison between the original and the updated interval of uncertain parameters

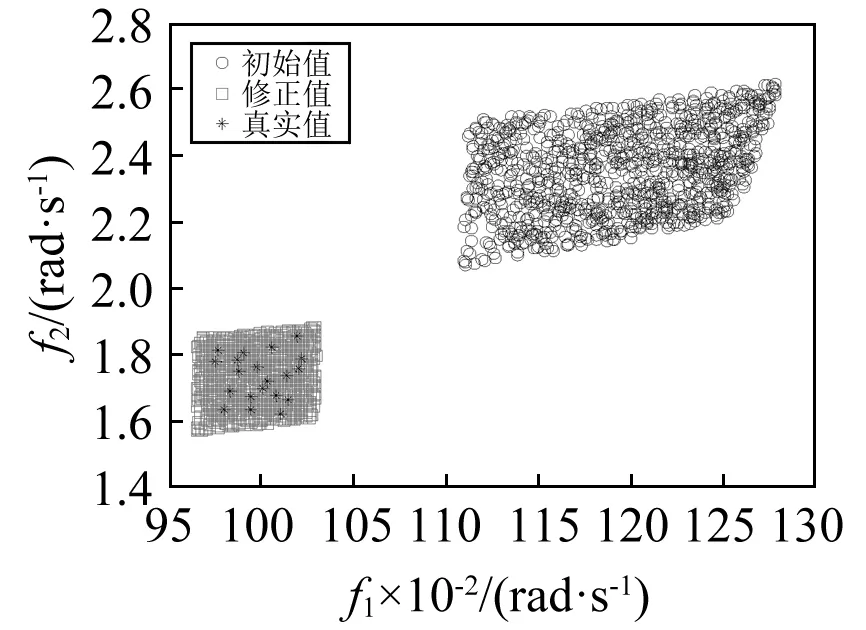
图7 修正前后系统固有频率计算结果与试验结果比较Fig.7 Comparison between the simulation and the experiment frequency results

3.2 反射镜架结构的参数识别

神光III光机装置是具有48路光束的对打靶精度有极高要求的惯性约束聚变装置，该装置有276个反射镜架系统，而反射镜架在环境激励下的稳定性是影响整个装置稳定性的关键因素[22]。本文考虑如图8所示的典型镜架系统，该系统有镜框组件和镜架支撑两部分组成。

镜架支撑结构的材料为钢，名义杨氏模量为200 GPa，密度为7 850 kg/m3，泊松比为0.3。镜框组件中镜片的材料为K9玻璃，名义杨氏模量为80 GPa，密度为2 510 kg/m3，泊松比为0.21。整个镜架系统约1.32 m高。

图8 反射镜架结构示意图Fig.8 Sketch map of the transport mirror system

镜架系统的不确定性主要是其底部与基础安装波动以及镜架支撑焊接工艺的差异带来结构刚度的不确定性，导致其动力学特性具有不确定性。为了研究不确定性对系统固有频率的影响，对同类型的镜架系统开展了10次模态试验。在感兴趣的频率范围内，有三阶模态，其影响结构的振动环境下的动力学响应。因此，开展动力学响应计算前应对该三阶模态进行模型修正。通过模态试验获得结构前两阶弯曲频率的10个样本，如表1所示。

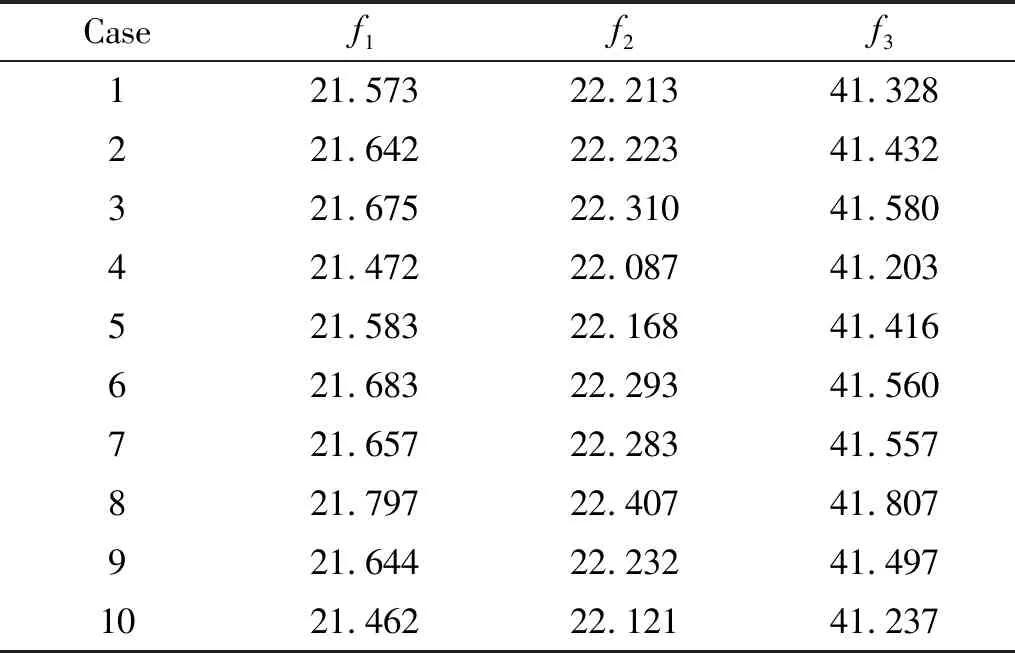
表1 镜架结构频率试验值样本

在ANSYS中采用SOLID185单元及SHELL181单元建立结构的有限元模型，如图9所示。结构前三阶计算模态振型如图10所示。

图9 镜架结构的有限元模型Fig.9 FE model of transport mirror system

图10 镜架结构前三阶模态振型Fig.10 Modal shapes of transport mirror system

安装带来的刚度不确定性在模型中用镜架支撑底部材料弹性模量E1表征，焊接不确定性用镜架支撑底部材料弹性模量E2表征。不确定性参数识别就是识别区间量E1与E2。

假定E1与E2的初始区间值分别为[1.0,1.5]×1011Pa 与[1.8,2.0]×1011Pa。首先根据式(2a)求出试验结果的中值，再根据图1所示区间参数中值优化流程，开展E1与E2的中值识别，经过6步迭代即收敛，且每个迭代步中所建立的响应面模型的R2>0.999，E1与E2中值迭代收敛情况如图11所示。

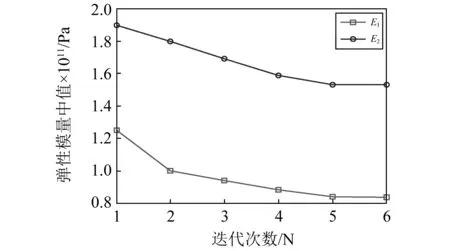
图11 弹性模量中值收敛情况Fig.11 Convergence curve of the mean of elastic modulus

根据图2所示参数区间半径优化流程，通过6步迭代即收敛，E1与E2半径的迭代收敛情况如图12所示。

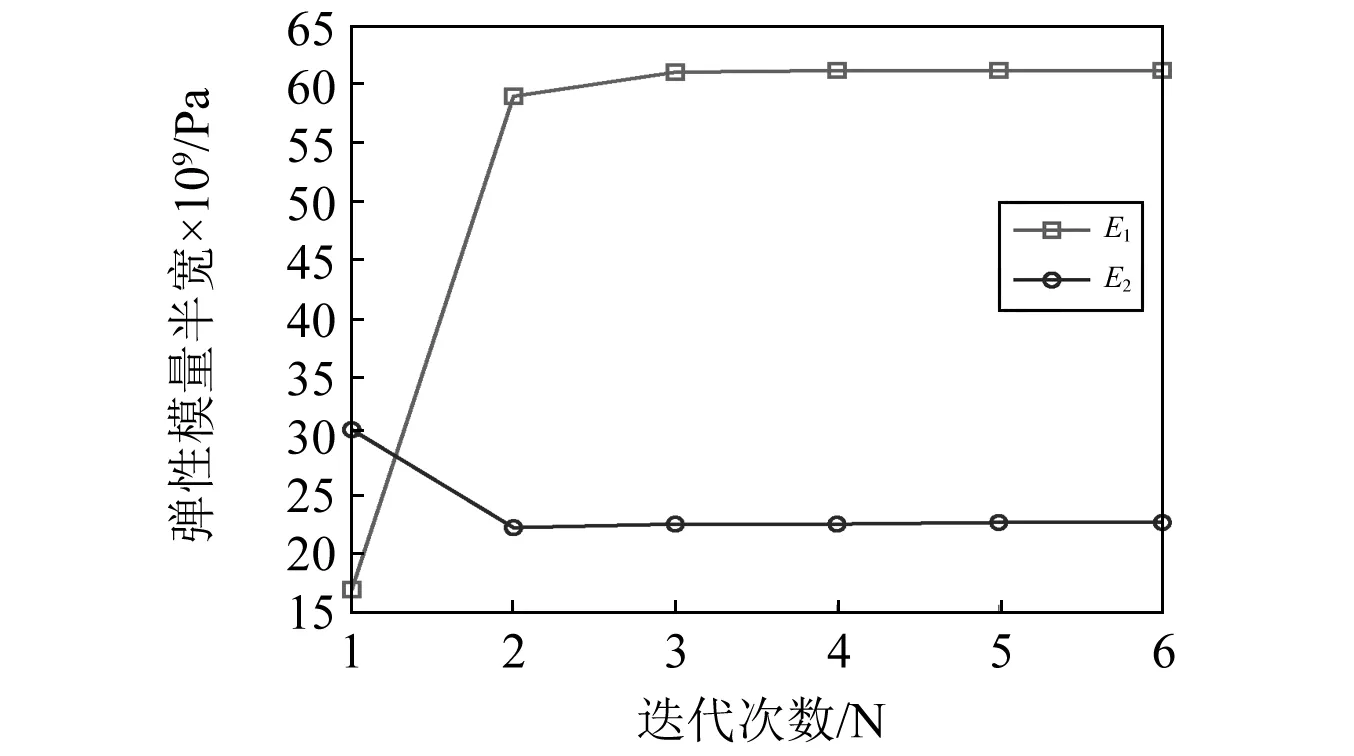
图12 弹性模量半径收敛情况图Fig.12 Convergence curve of the radius of elastic modulus

图13为修正前后不确定性参数区间的比较。根据待修正参数修正前后的区间值，采用均匀分布的拉丁超立方抽样方法构造1 000个随机样本，并计算反射镜架系统的前三阶固有频率，并与试验数据进行比较，散点图如图14所示。并且，根据1 000个样本估算系统前三阶固有频率的95%置信区间，并将其作为系统前三阶固有频率的区间，与试验结果的比较如表2所示。

从图14与表2可知，修正结果与试验结果吻合良好，且修正后的频率范围与修正前相比显得更符合工程实际。

图13 不确定性参数修正前后取值的比较Fig.13 Comparison between the original and the updated interval of uncertain parameters

图14 修正前后固有频率计算结果与试验结果比较Fig.14 Scatter map of the first three natural frequencies

模态试验区间/Hz初始计算区间/Hz误差/%修正区间/Hz误差/%1[21.46,21.80][23.39,24.42][8.99,12.02][21.45,21.79][-0.07,-0.04]2[22.09,22.41][24.05,25.01][8.87,11.60][22.08,22.42][-0.04,0.05]3[41.20,41.81][44.47,46.12][7.94,10.31][40.93,41.55][-0.66,-0.62]

3.2 讨 论

有限元模型修正与参数识别的时间主要取决于有限元模型的计算时间，在考虑不确定性时镜架系统的模型修正仅在第一步中值修正中开展了有限元计算。在构建响应面的每次迭代步中有9个样本，经过6个迭代步，故总共需要开展54次有限元模态计算。但是，如果不用代理模型，仅确定性的模型修正就需要开展上百次有限元计算，而考虑不确定性时，有限元计算次数会更多，因此，本文基于响应面与灵敏度分析的区间不确定性模型修正是高效的。

4 结 论

(1)不确定性在工程实际中广泛存在，针对考虑不确定性的动力学模型参数识别，本文提出了模型中区间不确定性参数识别的分步实施方法，第一步基于响应面模型对区间参数中值进行修正，第二步基于响应面模型并结合灵敏度分析实现区间参数的半径修正，并给出了两个修正过程的实施流程。由于采用响应面模型，可以大幅提高修正效率。

(2)在该思想下开展不确定性参数识别，在第一步中传统确定性的动力学参数识别与模型修正方法均可使用，便于实际应用。而且，提出首先对试验小样本采用核密度估计方法进行合理的区间估计，这使得参数识别结果对工程结构的计算预测更具有普遍指导意义。

(3)针对本文所提出的区间不确定性参数识别方法，通过两个算例对参数识别方法与流程进行了展示，识别结果与试验结果吻合良好。

(4)本文提出的分步实施的区间不确定性参数识别方法可有效避免区间优化导致的收敛困难，并提高参数识别效率，且在实际工程中易于实施。