基于随机有限元的无砟轨道服役可靠性分析

李再帏， 张 斌， 雷晓燕， 高 亮

(1.上海工程技术大学 城市轨道交通学院, 上海 201620；2. 华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；3. 北京交通大学 土木建筑工程学院, 北京 100044)

无砟轨道结构作为高速列车的行车基础，其服役状态直接关系到运营安全。在无砟轨道日常养护维修中，由于其扣件、轨道板、砂浆层等构件相对比较稳定，不易产生较大的变化，检测与维修的重点往往集中于轨道几何形位[1]。所以，研究和分析轨道不平顺对无砟轨道服役可靠性的影响具有一定的理论价值和实践意义。

为了深入的分析和控制无砟轨道服役可靠性，国内外学者从结构部件强度与设计理论、部件损伤、疲劳效应等多方面进行了研究，并采用了概率分析、一次二阶矩、响应面等分析方法。如文献[2]采用概率统计方法对Ⅲ型轨枕的可靠度及影响因素进行了讨论。文献[3]分析了在列车荷载及温度梯度荷载作用下无砟轨道的横向可靠度，利用一次二阶矩法对可靠度指标进行验算。文献[4]利用多重叠合梁模型对CRTSⅡ型无砟轨道板产生开裂病害后结构可靠度进行分析，通过蒙特卡罗抽样算法得到轨道板弹性模量、轮载等随机变量的结构失效概率。文献[5]基于可靠度理论构建了CRTSⅢ型无砟轨道结构耐久性与安全性评价体系，给出了混凝土碳化、冻融氯离子侵蚀等因素作用下结构的可靠度。文献[6]则采用了响应面方法对无砟轨道结构部件损伤条件下结构的可靠性进行分析。文献[7]分析了冻融条件下无砟轨道结构的疲劳可靠性度。这些研究得到了部分控制无砟轨道服役可靠性的因素及养护维修策略，深化了对无砟轨道服役可靠性的认识。但值得注意的是，上述研究多是利用相关结构设计参数展开，对目前相关维修检测数据应用较少，且研究方法多采用确定性分析的方法，对随机分析方法应用较少。与实际的无砟轨道结构服役状态具有一定的差别。所以，有必要采用随机理论相关方法对无砟轨道服役可靠性进行研究。

本研究利用车辆单元和轨道单元的有限元模型，采用神经网络模型进行轮轨关系映射，利用轮轨动力学随机因素构建无砟轨道服役极限状态方程，通过蒙特卡洛混迭建模方法分析轨道不平顺对无砟轨道服役可靠性的影响，从而实现对无砟轨道服役状态进行定量化评估的目的。

1 无砟轨道结构可靠度相关概念

对无砟轨道服役可靠性而言，目前尚无一个统一的定义，既有规范和研究往往针对各自分析的问题进行概念界定。所以，根据相关成果[8-9]，本研究中将无砟轨道服役可靠性相关概念进行界定。

可靠性为无砟轨道结构在服役期限内保证列车安全平稳通过的能力。可靠度为可靠性的概率度量，即无砟轨道结构保证服役状态的概率；与其对应的轨道结构失稳则为失效概率。当无砟轨道整体或部分构件超过某一特定状态就不能满足相关设计规定的车辆-轨道系统安全行车的要求，该特定状态称为无砟轨道服役极限状态。

鉴于既有无砟轨道结构的偏安全性设计，在正常的服役限期内，其结构承载的应力与变形往往可以满足列车安全运营的要求。因此，本研究这里引入了轮轨动力学随机因素作为评判指标来评估无砟轨道服役状态。在轨道随机不平顺的激励下，轮轨系统的动力响应呈现了显著的随机特征[10]，其轮轨作用力可作为直接的特征向量。由于评估列车运行安全性标准中，多采用脱轨系数和倾覆系数作为评价指标[11]。所以，本文中这里采用这2个指标作为评估无砟轨道可靠性的标准,其对应的无砟轨道服役极限状态方程为

(1)

(2)

由上述两式可知，在轮轨系统随机因素(如轨道不平顺等)作用下，尚无法用明确的解析表达式来表征相应的无砟轨道服役极限状态方程，即方程隐式化问题。所以，本研究中，采用随机有限元方法对此问题进行研究和分析。

2 基于随机有限元-神经网络-蒙特卡洛的混迭建模方法

一般而言，随机有限元方法包含有限元一次二阶矩法和有限元蒙特卡洛法，前者只适合于弱非线性系统，而后者则适用于极限状态方程隐化的高度非线性系统[12]。因此，本研究中采用了有限元蒙特卡洛法进行分析求解，但由于此方法在求解节点数较多的非线性结构体系时，需要的运算量大、计算时间长的缺点，这里利用神经网络非线性映射能力强的特点，对轮轨系统响应量与输入量的映射关系进行逼近。

2.1 轮轨动力学有限元模型

利用有限元理论，建立车辆-轨道非线性耦合动力模型，将整个系统离散为车辆单元和轨道单元。其中，车辆单元为一个附有二系弹簧阻尼的多刚体动力系统，如图1所示。轨道单元为路基上CRTS II 型板式无砟轨道，如图2所示。

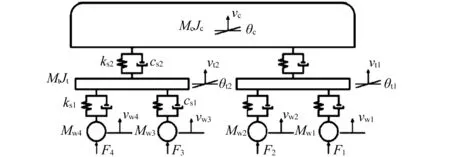
图1 车辆单元模型Fig.1 Vehicle element model

图1 中:Mc和Jc分别为车体质量与转动惯量；Mt和Jt分别为转向架质量与转动惯量；Mwi(i=1, 2, 3, 4)为第i个车轮质量；ks1和cs1分别为车辆一系悬挂刚度与阻尼；ks2和cs2分别为车辆二系悬挂刚度与阻尼；vc和vti(i=1, 2)分别为车体和前后转向架的沉浮运动竖向位移；θc和θti(i=1,2)分别为车体和前后转向架的点头运动角位移；vwi(i=1, 2, 3, 4)为第i个车轮的竖向位移；l1和l2分别为车辆固定轴距之半和车辆定距之半。

图2 CRTS II型板式轨道单元模型Fig.2 Track element model of CRTS II

图2中：u1和u4分别为钢轨的竖向位移；θ1和θ4分别为钢轨的转角；u2和u5分别为预制轨道板的竖向位移；θ2和θ5分别为预制轨道板的转角；u3和u6分别为水硬性混凝土支承层的竖向位移；θ3和θ6分别为水硬性混凝土支承层的转角；ksy1，ksy2和ksy3分别为无砟轨道扣件、CA砂浆和防水层的刚度；csy1，csy2和csy3分别为无砟轨道扣件、CA砂浆和防水层的阻尼。

利用有限元集成法可形成车辆-轨道耦合系统总刚度矩阵K、总质量矩阵M和总阻尼矩阵C，得到车辆-轨道耦合系统动力有限元方程

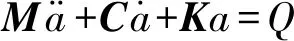
(3)

式(3)可以通过Newmark-β积分法实现数值求解[13-14]。

2.2 混迭计算模型

由式(3)可知，由于车辆及轨道单元节点数较多，特别是当轨道长度较长时，需要耗费大量机时进行轮轨动力学响应运算。而根据规范的可靠度指标的相关要求，应用蒙特卡洛法(MonteCarloSimulation，MCS)至少要进行1×105以上的运算次数，这无疑不利于对无砟轨道结构服役状态的及时评定。因此，本文这里引入人工神经网络模型对轮轨关系进行映射，以期在保证计算精度的前提下提高运算效率。

相关理论表明：在隐含层节点数充分大的情况下，单隐层的BP神经网络可以以任意精度逼近任何一个具有有限间断点的非线性函数。这里采用了三层BP神经网络结构进行轮轨关系映射，其中，输入变量为2种轨道不平顺(高低及轨向)、输出变量为2个即脱轨系数及轮重减载率极限状态方程值。根据文献成果与前期试算，将网络结构选为2-5-2结构，即包含5个隐含节点。

在此基础上，采用MCS进行计算，计算流程如图3所示。

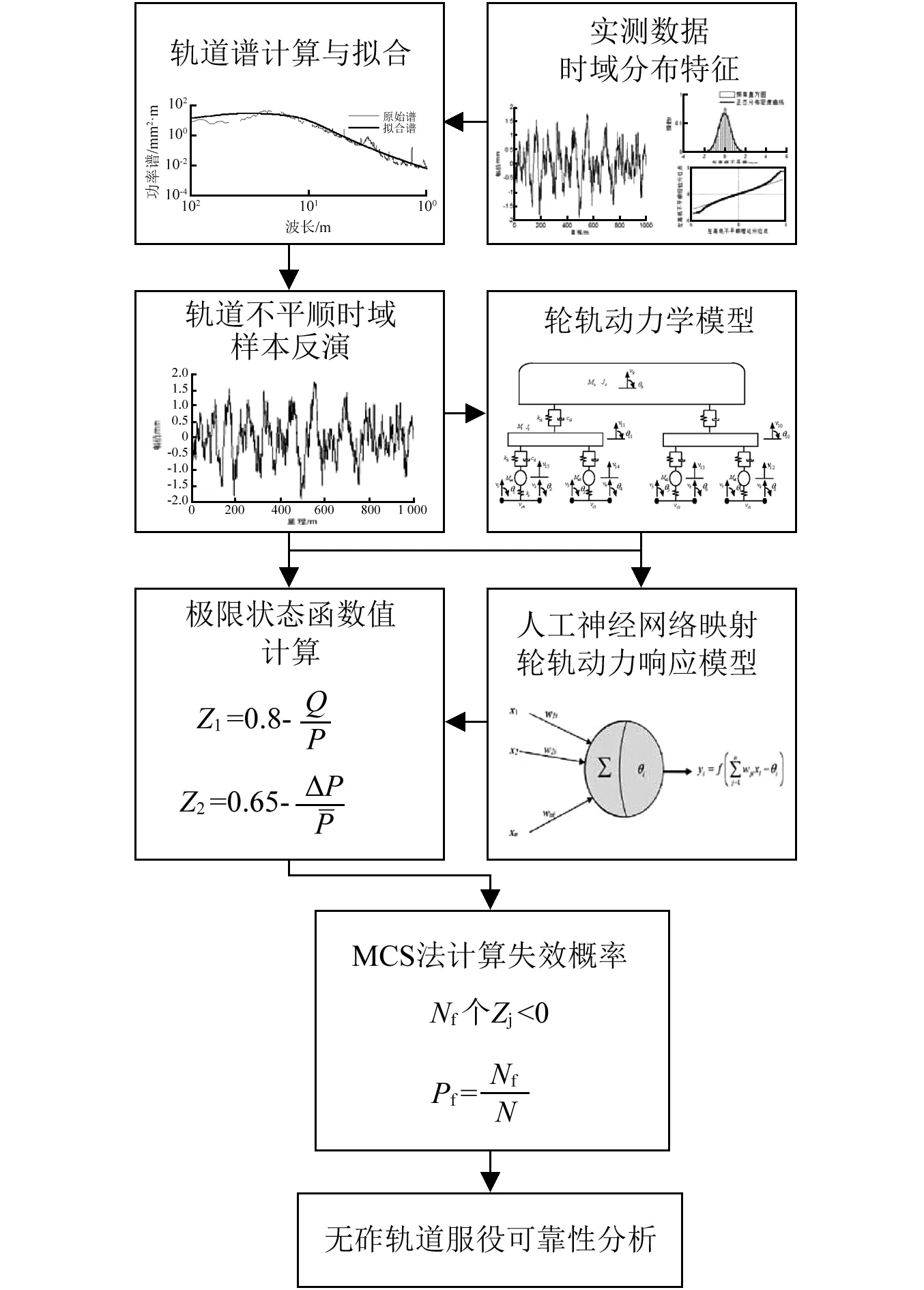
图3 混叠建模计算流程Fig.3 Calculation flow of hybrid model

具体计算步骤为：

步骤1轨道不平顺时域随机样本的生成，利用实测样本进行随机样本的拟合与反演；

步骤2基于车辆-轨道单元的轮轨动力响应及极限状态方程计算；

步骤3利用三层BP神经网络进行轮轨映射关系构建；

步骤4对轨道不平顺随机量进行N次时域反演，并采用映射模型进行极限状态方程值求解，得到N个Zj(j=1,2,…,N)值；

步骤5设在N个Zj中存在Nf个Zj<0，当N充分大时，无砟轨道结构的失效概率为

(4)

3 算 例

为了对本文所提分析方法进行验证，这里采用如下算例：高速列车为标准CRH 3C型动车组、运行速度为350 km/h，轨道结构为CRTS II型板式无砟轨道，基础为路基结构。

3.1 轨道不平顺的拟合与时域反演

根据动检车实测样本进行轨道不平顺统计特征计算，实测样本如图4所示。采用文献[15]方法进行轨道不平顺谱计算，获得样本轨道谱参数后，将其作为目标函数，并利用二进制小波方法进行样本时域波形反演。

时域样本的拟合结果和反演的时域样本如图5及图6所示。所采用的目标拟合公式为中国铁路7参数公式；拟合参数结果如表1所示。

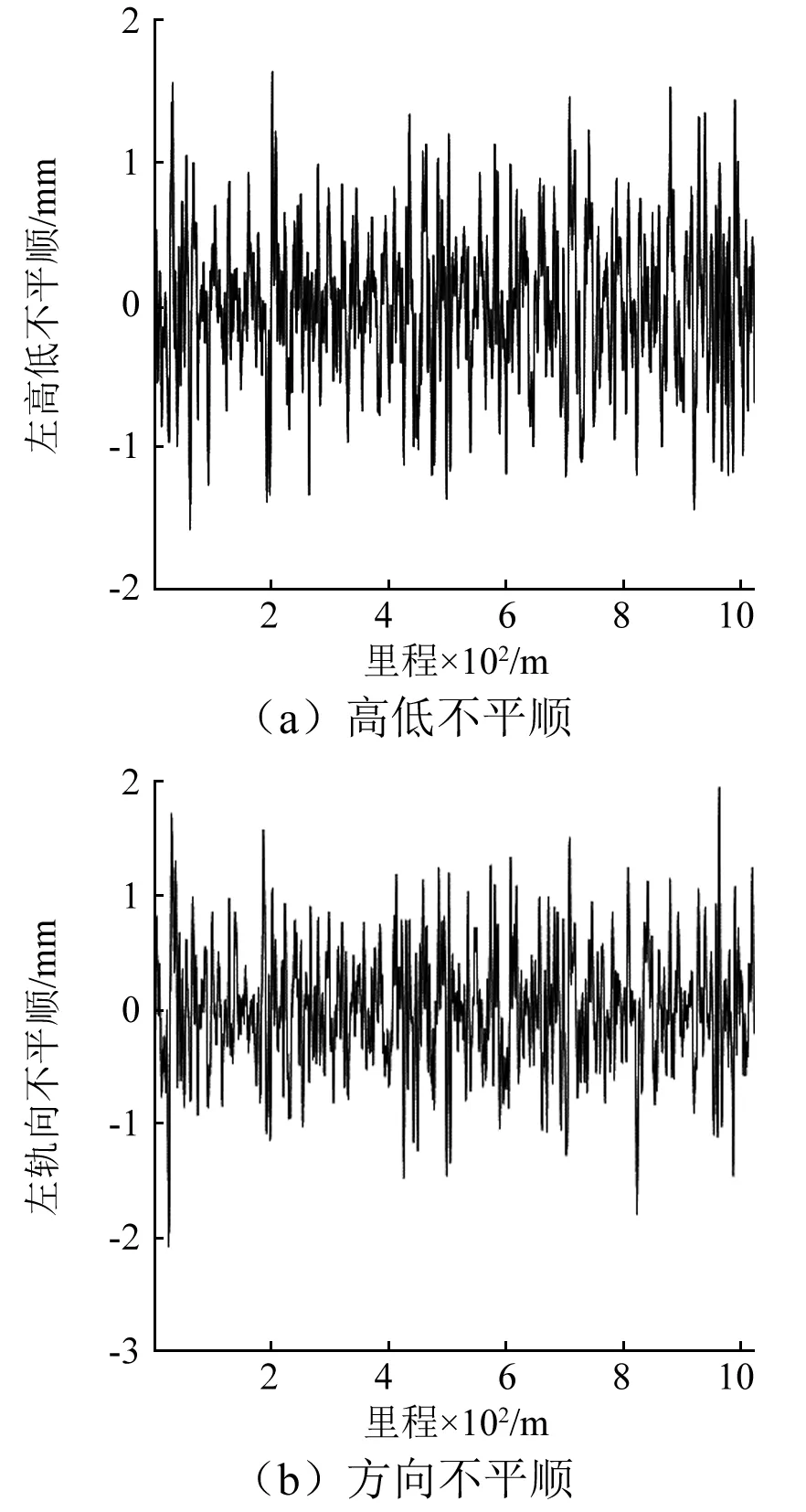
图4 轨道不平顺时域分布Fig.4 Time domain of track irregularity

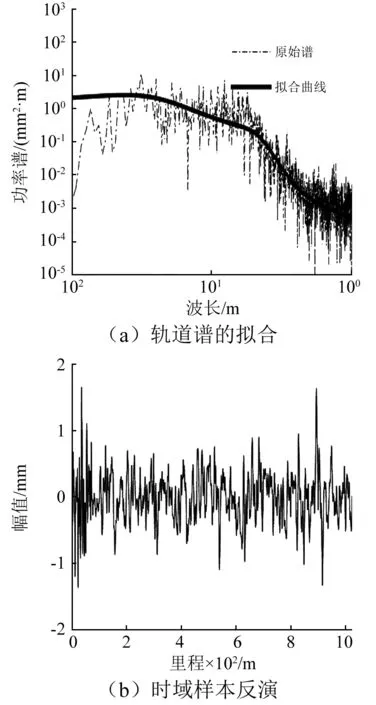
图5 左高低不平顺的拟合与时域反演Fig.5 Fitting and time domain inversion of left longitudinal irregularity

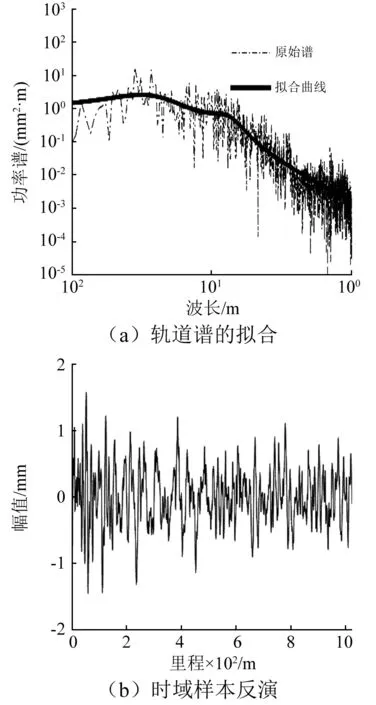
图6 左轨向不平顺的拟合与时域反演Fig.6 Fitting and time domain inversion of left alignment irregularity

参数ABCDEFG左高低0.000 35-0.611 990.136 97-0.408 770.056 36-0.002 920.000 09右高低0.000 67-0.685 120.159 21-0.449 30.066 8-0.002 640.000 07左轨向0.001 62 -0.208 84 0.016 93 -0.314 88 0.034 60 -0.001 45 0.000 03 右轨向0.001 77 -0.260 22 0.018 79 -0.320 41 0.035 00 -0.001 48 0.000 03

由以上图表可知，所得的拟合谱参数可以较好地反映出原始轨道不平顺的时频特征。因此，采用表1参数进行轨道不平顺时域波形的反演。

3.2 神经网络模型的训练

输入变量为随机生成的轨道不平顺样本，长度为1 000；输出变量为对应轮轨动力计算得到的脱轨系数及轮重减载率极限状态方程值。结果如图7及图8所示。

通过预先的大量试算，将BP神经网络迭代次数设为100、学习率为0.005、网络收敛目标为0.000 04。则神经网络预测结果如图9所示。

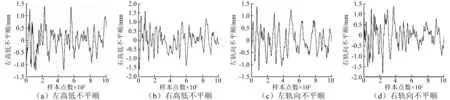
图7 神经网络计算输入参量Fig.7 Inputs of BP neural network model

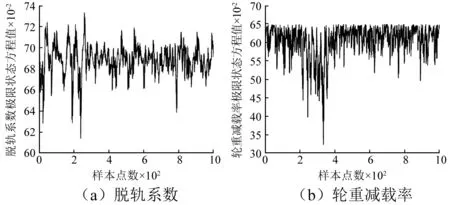
图8 神经网络计算输出参量Fig.8 Outputs of BP neural network model

图9 神经网络模型预测结果Fig.9 Predictions of BP neural network model

由图9可知，轮重减载率极限状态方程值的预测样本和实际样本相关系数为0.805、误差均方值为0.073，而脱轨系数极限状态方程值的则相关系数为0.767、误差均方值为0.023，说明预测样本与实际样本误差较小、且呈现强烈相关的特性。对比实际数据与预测数据的样本区间可知，两者之间幅值区间差别较小。所以，综上可得所采用的BP神经网络模型较为真实地反映了实际数据的变化趋势与幅值分布，可以采用BP神经网络建模方法对轨道不平顺与轮轨动力响应的关系进行映射，从而进行相应的动力计算，值得注意的是相关参数选择是模型逼近准确性的关键要素。

3.3 计算结果

利用建立的轮轨系统BP神经网络映射模型替代蒙特卡洛法中的轮轨动力学模型，进行无砟轨道结构服役安全性的可靠度和失效概率计算。

依据相关规范要求，CRTS II型板式无砟轨道属于铁路工程结构安全等级中的二级，对应的目标可靠度指标建议管理值为3.7即失效概率为1.078×10-4，则若要计算的可靠性指标满足上述要求，则至少要进行以上的次数1×105，为了尽可能的逼近真实解析解，本文这里选取计算次数为1×105。

为了对比分析，同样给出了利用传统轮轨动力学模型进行计算的结果，如表2所示。

表2 BP神经网络模型计算结果Tab.2 The calculations of BP neural network

通过上表可知，利用BP神经网络法映射模型可以获取轨道结构服役安全性的可靠指标和失效概率，所得的无砟轨道服役可靠性指标值满足相关规范要求；其计算结果与采用传统模型得到的近似解析解对比分析可知，所得的计算结果工况所计算精度较采用轮轨理论模型差，这主要是由于在BP神经网络映射模型逼近求解过程中，产生累积误差，导致其所计算的可靠指标有一定的偏差；但比较计算时间可知，采用BP神经网络可以有效地节约计算时间，显著地提升算法的效率。值得注意的是，由于BP神经网络的建模过程中对参数依赖性较高，如参数优化不良，则会产生算法不收敛或收敛速度慢等问题，因此，此算法的普适性相对较差，应用前需要进行大量的参数试算。

综上，当工程的要求精度不高或轨道服役状态相对较好时，可以采用此方法进行相应的无砟轨道结构服役安全性检算。

4 结 论

本文从轮轨动力学随机因素构建无砟轨道服役极限状态方程，采用轮轨动力学有限元、BP神经网络和蒙特卡洛混迭建模的方法，分析了无砟轨道的服役可靠性，得到以下结论：

(1)无砟轨道服役可靠性评估需要考虑轮轨动力学作用。

(2)可以采用随机有限元和神经网络相结合的方法对无砟轨道结构服役可靠性进行定量计算。

(3)在现有的轨道不平顺状态水平下，无砟轨道结构服役状态可以满足高速列车安全运行的要求。

(4)建议将结构服役安全性验算指标纳入到养护维修体系中，以便更加全面有效地保证高速铁路的运营安全。