压电智能结构振动系统未知扰动估计

伍彬艺， 秦现生， 张顺琦, 王战玺, 白 晶, 李 靖

(1.西北工业大学 机电学院, 西安 710072; 2.上海大学 机电工程与自动化学院, 上海 200444)

振动会降低结构系统精度,有时会导致结构出现严重损伤,造成灾难性事故[1-2]。扰动是导致系统振动的主要因素,如果扰动信息已知，可通过采用合适的反馈控制器对结构系统的振动进行有效的抑制[3]。但是在很多实际工程应用中,作用在结构上的扰动由于受工作环境的限制很难被直接测量[4-5]。因此,对振动系统的外部未知扰动进行准确估计具有十分重要的理论意义和应用前景。

扰动力估计属于载荷识别的范畴,目前有两种主要的方法，即频域法和时域法。在载荷识别的频域法方面,Barlett等[6]在频域内用加速度响应对作用在直升机桨穀中心动态载荷进行了识别,开创了动态载荷识别的先例。Hillary等[7]通过采用两个频率相同但幅值不同的正弦力作为激振研究了悬臂梁载荷识别问题,结果表明测量噪声是载荷识别结果不佳主要因素。频域法的研究较早，理论发展比较成熟,但也存在一些限制，如要求信号样本具有一定的长度和只适合静态及平稳载荷。

与频域法相比,时域法可对包括冲击载荷在内的各类非平稳动态载荷进行识别，识别结果有明确的物理意义,具有广阔的工程应用前景。Desanghere等[8]将模态坐标变换方法引入到动态载荷识别过程,建立了动态载荷识别的时域方法。Ory等[9]提出了离散系统的动态载荷识别方法,并对飞行器所受的飞行载荷进行了识别。但上述各种方法都要求测量点的数目不小于模态数，这在许多实际应用中很难实现。为了解决这个问题，Müller[10]提出了一种比例积分(Proportional Integral, PI)观测器来估计振动系统的未知扰动(为区分本文方法，该方法简称为PI-Müller),该比例积分观测器只要求测量点的数量不少于未知的扰动数量。

压电智能结构是将压电材料集成到基本结构中组成的一种主动智能结构。这种结构同时具有传感和驱动功能,具备良好的机电耦合性能,在结构振动控制中有着广泛的应用前景[11]。Zhang等[12-13]在普通PI观测器基础上提出了更加通用的比例积分(Generalized Proportional-Integral，GPI)观测器，实现高阶频率未知扰动的预测，并对压电层合薄壁结构振动进行了有效地抑制。

测量噪声在工程使用中是实际存在的,且无法得到完全抑制,对扰动估计系统的性能有较大的影响。上述研究包括PI，GPI观测器在内的大多数扰动估计方法都没有考虑测量噪声的影响，这限制了其应用前景。为此,在传统PI观测器的基础上，本文提出了一种采用卡尔曼滤波器的扰动估计方法(PI-Kalman)。该方法以分布式压电智能结构为研究对像，实现未知动态载荷的估计。仿真结果表明在考虑测量噪声的情况下，与传统PI观测器相比，该扰动估计方法具有更好的估计性能。

1 压电智能结构的动态模型

通过应用有限元方法和哈密顿原理，能够得到压电智能结构的机电耦合动力学模型[14]。

(1)

Kφuq+Kφφφs=0

(2)

式中：Muu,Cuu,Kuu,Kuφ,Kφu和Kφφ分别为质量矩阵、阻尼矩阵、刚度矩阵、压电耦合刚度矩阵、耦合容量矩阵和压电容量矩阵；另外，q,Fue,φa,φs分别为节点的位移向量、外部力向量、执行器控制电压向量和传感器输出电压向量。

一般的有限元模型通常有几百个自由度, 考虑到高阶模态对低频响应的影响较小,为了减少计算时间，使用截断模态矩阵Sr来降低分析问题的自由度规模。

(3)

(4)

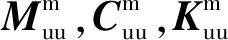
考虑到扰动的影响，智能结构的状态空间模型可以表示为

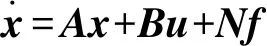
(5)

y=Cx+n

(6)

(7)

(8)

(9)

(10)

2 外部未知扰动的估计

2.1 扰动虚拟模型

从理论上讲，任何周期性的未知扰动都可以用傅里叶级数表示

(11)

式中：ω为余弦和正弦基函数的角频率。以傅里叶级数的有限项作为基函数向量v(t)，则未知扰动可以近似的表示为

f(t)≌Hv(t)

(12)

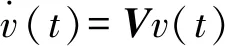
(13)

式中：H，V分别为扰动虚拟模型的输出矩阵和系统矩阵,它们的值取决于所选取的傅里叶级数的项数。当使用阶跃函数作为未知扰动的基函数时,即为比例积分观测器,此时H，V分别为单位阵I和零矩阵0

H=I,V=0

(14)

2.2 扩展系统和扩展观测器系统

(15)

y=Cexe+n

(16)

式中：Ae，Be，Ce分别为扩展系统的系统矩阵，控制矩阵和输出矩阵。

(17)

Ce=[C0]

(18)

根据经典的Luenberger观测器结构，扩展观测器系统的状态空间模型可以表示为

(19)

(20)

2.3 估计误差分析

为了确保扩展观测器系统稳定,对动态模型的估计误差进行分析

(21)

根据式(15)和式(19)，可以得到扩展系统估计误差的系统方程

(22)

估计误差的系统特性只与扩展系统的系统特性和观测器增益有关。因此，选择合适的观测器增益使性能指标函数J最小就显得尤为重要

J=limt→∞(exe(t)Texe(t))=min

(23)

2.4 观测器增益设计

PI-Müller扰动估计方法设计的观测器是一种理想的观测器模型。该方法在设计观测器增益时，没有考虑测量噪声的影响，影响了其状态观测精度和扰动估计性能。卡尔曼滤波器在系统特性和测量噪声的统计特性都已知的情况，能够实现最优估计，经常被用来通过降低测量噪声的影响来估计系统状态变量。针对PI-Müller扰动估计方法在测量噪声不能忽略的应用场合下性能受限的情况，本文将PI-Mülle方法和卡尔曼滤波器结合起来，提出了PI-Kalman方法。该方法在进行观测器增益设计时，选择卡尔曼滤波器增益作为观测器的增益以实现对测量噪声的补偿。

2.4.1 PI-Müller方法

传统的PI-Müller方法是一种理想的观测器模型，不考虑噪声的影响，观测器的增益L可以表示为

(24)

根据线性模型的李雅普诺夫稳定性判据，对于任意的对称正定矩阵Q，存在唯一的对称矩阵P满足下列瑞利代数方程

(25)

(26)

解此标准瑞利方程，可以得到Pk的值, 再根据式(24)可以得到扩展观测器系统的增益值。

2.4.2 PI-Kalman方法

当传感器输出信号包含测量噪声时，基于卡尔曼滤波的观测器增益可以表示为[15]

(27)

式中：RN为测量噪声的均方差；P为唯一满足下列代数瑞利方程的对称正定矩阵。

(28)

同样，式(28)也可以转换为标准的代数瑞利方程。解标准瑞利方程，可以得到Pk的值, 再根据式(27)可以得到扩展观测器系统的增益值。此外，通过调用Matlab中的函数Kalman函数也可以得到扩展观测器系统的增益值。

2.5 扰动估计系统

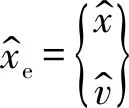
(29)

(30)

3 扰动估计仿真

使用集成8个压电片的悬臂梁(尺寸、结构和布局如图1所示)进行仿真测试。悬臂梁主结构材料为弹簧钢，尺寸为425 mm×25 mm×0.8 mm。压电块的尺寸为25 mm×25 mm×0.25 mm，圧电片之间的间距相同且都为25 mm，极化方向指向主结构的外法线方向。当悬臂梁上的应变变化时，压电片作为传感器产生输出电压。此外，如果没有其它说明，外部未知扰动作用在悬臂梁的A点。

图1 悬臂梁尺寸及结构布局Fig.1 The dimension and structure layout of a cantilever beam

将悬臂梁主结构划分为17个单元, 每个单元有8个节点, 每个节点有5个机械自由度和一个电自由度, 建立有限元模型。根据建立的有限元模型，在Matalb通过程序计算可以得到相应的模态质量矩阵、模态阻尼矩阵和模态刚度矩阵，再根据与状态空间模型的对应关系，可以得到系统矩阵A、输入矩阵B、扰动影响矩阵N、控制矩阵C。然后,可以使用PI-Müller和PI-Kalman方法来求解观测器增益。获得观测器增益后, 利用采集的压电传感器输出信号作为输入信号,根据扰动估计系统的状态空间方程式(29)～式(30),对外部未知的扰动进行估计。为了减少计算时间,动态有限元模型只保留前12阶模态。悬臂梁的主结构和圧电片的材料性能参数见表1。

为了表述方便, 在这里对几个定义进行说明。传感器理想输出信号是指不考虑测量噪声的传感器输出信号，传感器实际输出信号是指包含测量噪声的传感器输出信号。输出信号的信噪比是指传感器理想输出信号与测量噪声的功率比。

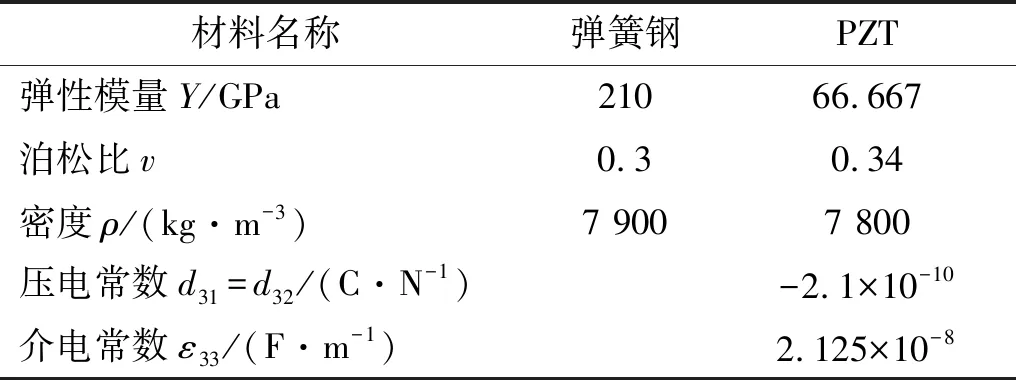
表1 悬臂梁的材料参数

3.1 阶跃扰动

阶跃扰动信号幅度为0.1 N，0.25 s时作用在悬臂梁的A点。在本次仿真中，施加的测量噪声为均值和方差为已知的高斯白噪声。在考虑测量噪声的情况下,为了分析PI-Müller方法和PI-Kalman的扰动估计性能,我们使用不同位置的压电传感器的输出信号进行扰动估计。压电传感器1、压电传感器3、压电传感器5、压电传感器7的输出信号及估计的扰动信号如图2～图5所示。从图2(a)可知，由于该处测量位置的弯矩及正应力较大，压电传感器1实际输出信号相对理想输出信号有较小的幅度起伏，信噪比较大。利用传感器1的实际输出信号，使用PI-Müller和PI-Kalman估计的扰动信号如图2(b)所示。从图2(b)可知，使用PI-Müller和PI-Kalman估计的扰动，上升时间都较小，这表明两种扰动估计方法都具有较好的响应速度。但由于PI-Kalman方法考虑了测量噪声的影响，与PI-Müller方法相比，使用该方法估计的扰动更为平滑也更接近于实际的阶跃扰动。压电传感器3的输出信号及其估计的扰动信号如图3所示。从图3可知，由于测量噪声的影响，传感器的实际输出信号包含一些毛刺，其信噪比相对测量位置1来说有一定的降低，但依然较高。对比PI-Müller和PI-Kalman估计的扰动信号, 可以发现PI-Müller估计的扰动信号幅度起伏较大。这样的事实表明，当传感器输出信号包含测量噪声时，PI-Kalman扰动估计方法能取得更好的估计效果。压电传感器5的实际输出信号，如图4(a)所示。受测量噪声的影响较大，相对传感器1和传感器3，其信噪比下降的较多。使用压电传感器5估计的扰动信号如图4(b)所示。从图4(b)中可知，与PI-Müller估计的扰动信号相比，PI-Kalman估计的扰动信号的上升时间接近，但有更小的超调量和稳态误差。压电传感器7的输出信号及估计的扰动信号如图5所示。从图5可知，由于本测量位置弯矩和正应力小，传感器理想输出信号弱，受测量噪声影响最大，其信噪比在4个测量位置最小。相对传感器1、传感器3、传感器5来说，不管是采用PI-Müller方法和PI-Kalman方法，使用传感器7估计的扰动信号有更长的上升时间，更大的超调量和稳态误差。另外，与PI-Müller估计的扰动相比，采用PI-Kalman方法估计的扰动的上升时间更长，超调量和稳态误差更小。

图2 使用压电传感器1估计的阶跃扰动Fig.2 Estimated step disturbances with piezoelectric sensors 1

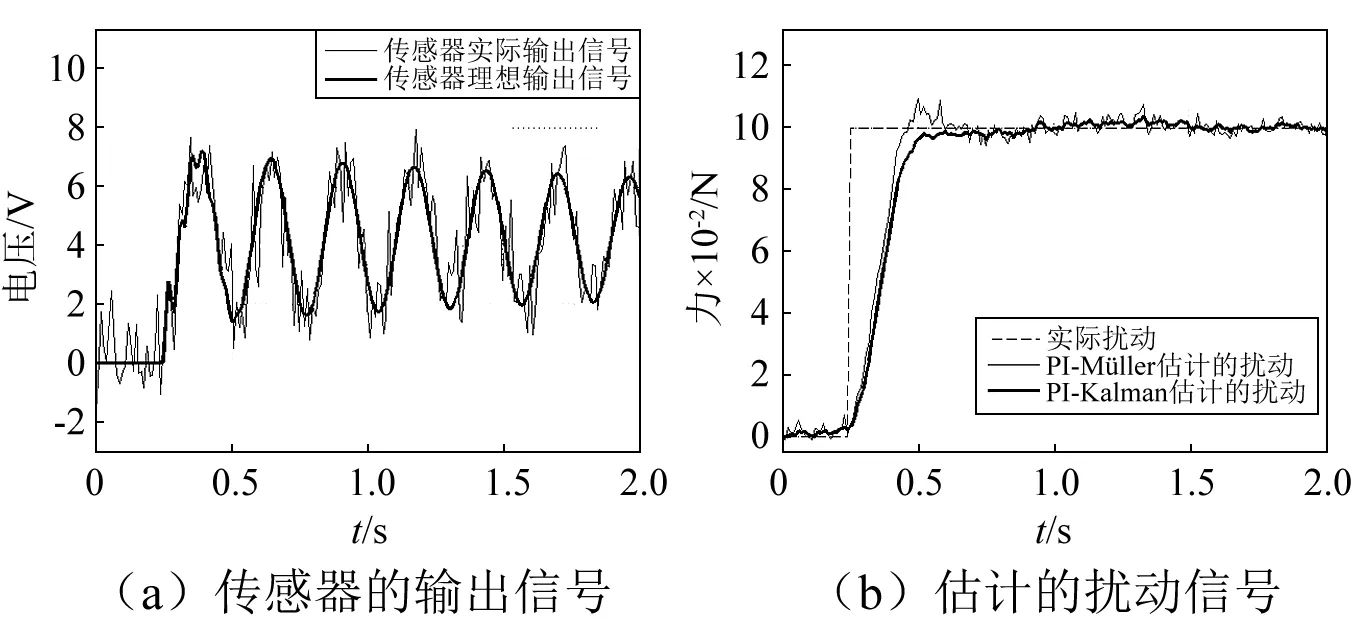
图4 使用压电传感器5估计的阶跃扰动Fig.4 Estimated step disturbances with piezoelectric sensors 5

图3 使用压电传感器3估计的阶跃扰动Fig.3 Estimated step disturbances with piezoelectric sensors 3

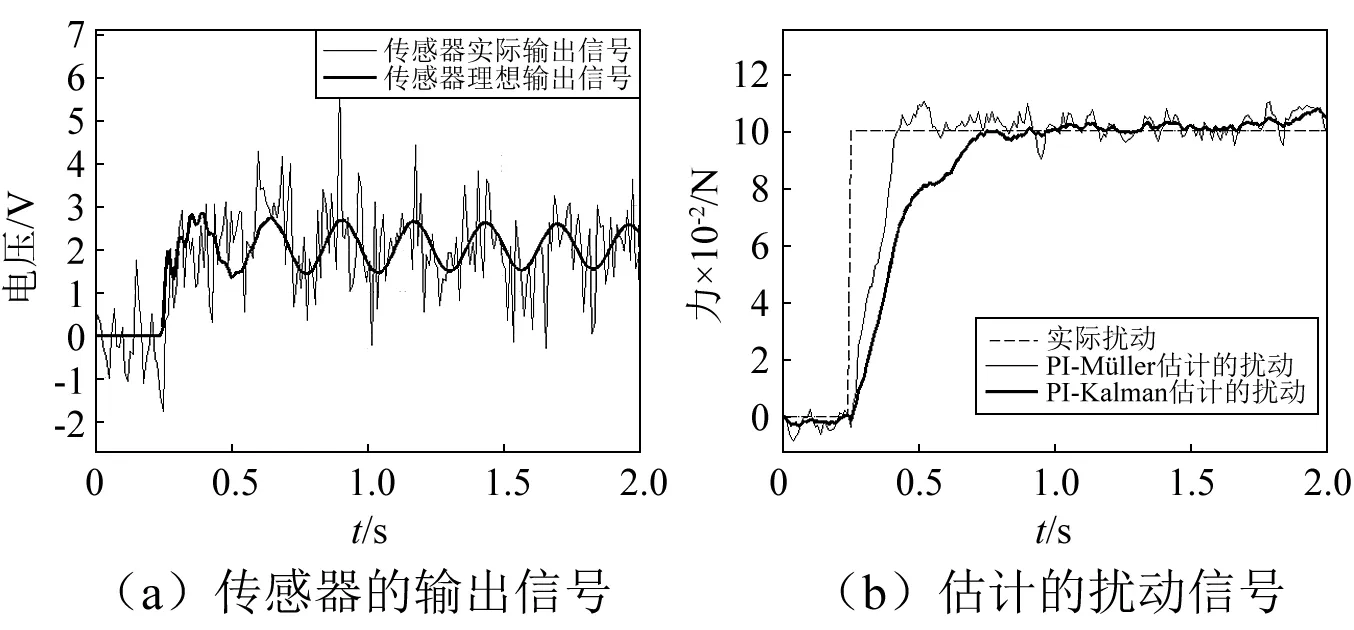
图5 使用压电传感器7估计的阶跃扰动Fig.5 Estimated step disturbances with piezoelectric sensors 7

3.2 谐波扰动

为了进一步验证PI-Kalman方法对不同类型的外部扰动信号的估计性能，我们将谐波扰动信号f(t)=0.1cos 2πt加载在悬臂梁的A点，利用压电传感器1的输出信号，分别使用PI-Müller方法和PI-Kalman方法对外部未知扰动进行估计。传感器的输出信号和估计的扰动信号如图6(a)和图6(b)所示。从图6(a)可知，含有测量噪声的传感器实际输出信号和传感器理想输出信号波形相似，但包含更多的毛刺。从图6(b)可知，PI-Müller和PI-Kalman两种扰动估计方法估计的扰动与实际扰动相比，波形相似，都存在一定的时延。但由于PI-Kalman方法考虑了测量噪声的影响，与PI-Müller方法相比，使用该方法估计的扰动更为平滑。

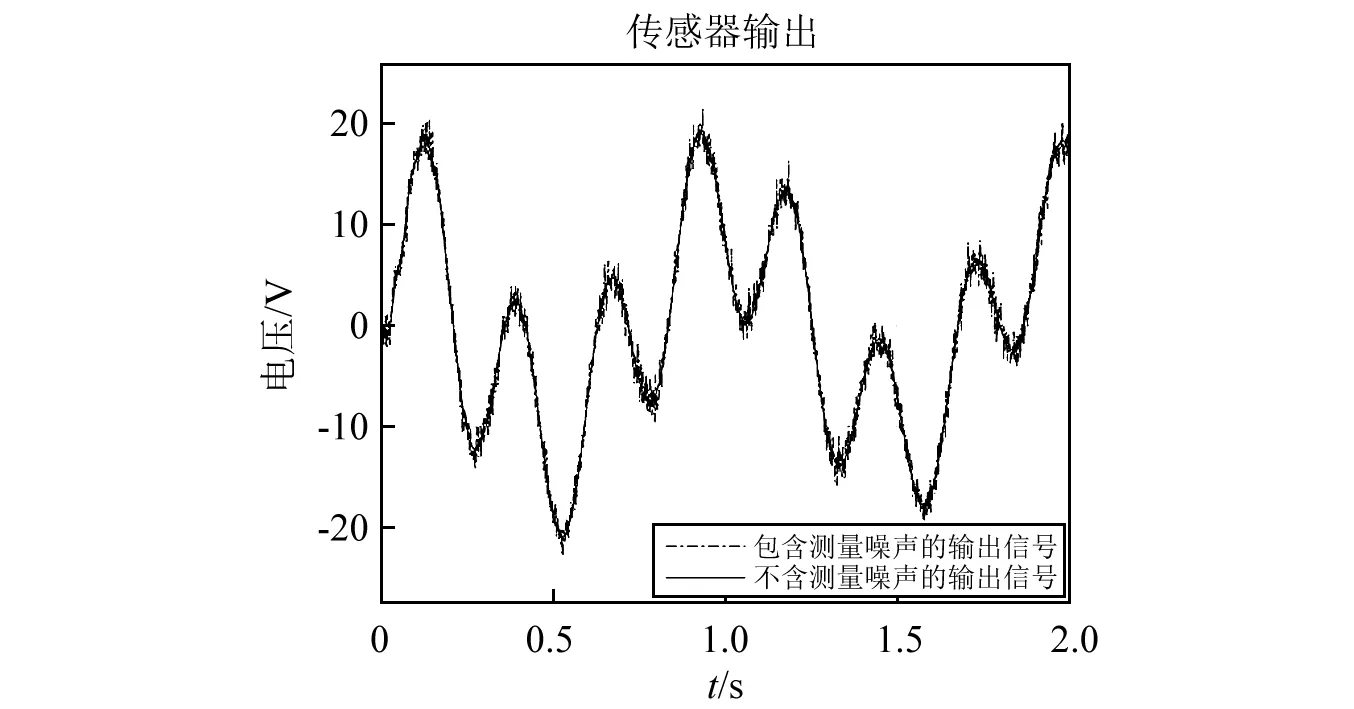
(a)传感器1的输出信号

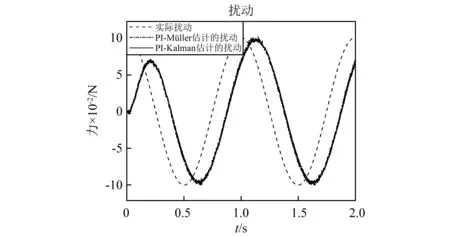
(b)估计的扰动信号图6 使用压电传感器1估计的谐波扰动Fig.6 Estimated harmonic disturbances with piezoelectric sensors 1

4 结 论

本文提出了一种基于卡尔曼滤波器的智能结构比例积分扰动观测器，并应用于分布式压电智能结构对外部未知扰动的估计，通过仿真得出以下结论：

(1)在测量噪声存在的情况下，本文提出的PI-Kalman方法对外界未知扰动具有良好的估计性能。与传统PI-Müller方法相比，该方法估计的扰动更加平滑。

(2)测量位置对扰动估计质量产生了重要影响，选择理想的位置能得到较好的扰动估计效果。同时测量信号信噪比对扰动的估计也有较大影响。