质谱成像中的计算策略综述

许 光，甘胜丰，李建军，杨 莉

（1．湖北第二师范学院计算机学院，湖北武汉430205；

2．Department of Computer Science，Texas A＆M University Corpus Christi，TX，USA 78412；3．Human Health Therapeutics，National Research Council Canada，Ottawa，Ontario，Canada K1A0R6）

1 前言

质谱成像（MSI）可以把生物组织切片上获取的不同位置的质谱数据直接生成二维或三维图像中的像素点。近年来，发展迅速的最常见的MSI技术是基质辅助激光解吸电离－飞行时间质谱成像（MALDI成像）［1－2］。其他MSI方法包括二次离子质谱（SIMS）和解吸电喷雾电离（DESI）也被广泛应用。对于 MSI数据分析，除了主成分分析（PCA）等常用算法外，近年还出现了大量新颖的计算策略和方法［3－5］。MSI的生物学和临床应用包括组织疾病（如癌症）分类和诊断、生物标记物研究、组织分子鉴定（如代谢组学内容）和药物开发［1，6］。在MSI技术中，由多个质谱谱图数据组成的空间数据矩阵可由MALDI质谱仪产生。每张质谱来自于整个组织切片中具有特定空间位置的样本点。由于图像的每个空间位点可显示为具有x和y坐标的像素点，MSI数据矩阵包含三个维度，即空间坐标x、y和每个质谱数据中的质荷比（m／z）。图像的颜色是根据每个样品的特定位点的分子丰度确定的。MSI图像分辨率通常可以达到20μm，这意味着一个组织切片可以产生数万个像素点。如果从每个谱图中提取超过一百个信号峰，那么整个图像将具有超过一百万个数据点。

因为处理MSI数据集中不同像素的质谱是非常具有挑战性的。我们在这篇综述首先讨论原始数据预处理的算法，包括数据归一化、校正和m／z－图像去噪。我们随后讨论各种数据降维算法，包括线性降维方法（如PCA、独立分量分析、非负矩阵分解和最大自相关因子）、非线性降维方法（随机邻域嵌入法（SNE））和特征选择算法。我们还会总结MSI数据聚类和分类中的统计和机器学习算法。最后，我们回顾计算策略在MSI系统中的生物学应用以及近年来已发表的软件工具。

1 MSI数据预处理

1．1 谱图处理

MALDI－MSI超谱数据集是由大量质谱谱图组成，每个谱图是由位于整个样本区域内一个空间点的样本生成。图像中的一个像素点可以用一个MALDI－MS谱图来表示，该谱图包含具有不同m／z的分子离子的定量丰度信息。m／z和丰度值成对出现在质谱谱图中形成峰值。在信号峰检测和统计分析之前，预处理过程通常会被使用来修正数据从而获取更加规范的空间质谱数据集。

与传统的MALDI数据分析类似，MSI中的预处理方法也包括基线校正、平滑去噪、归一化等［7－8］。然而，与MALDI－MS数据相比，在一个MSI数据集中有数千或数万个质谱谱图。为了减小质量和丰度在不同质谱之间的偏差，校准相同离子在不同谱中的m／z值，有必要将它们的丰度值归一化为统一的尺度。人们通常选择均匀分布在所有样本像素中的分子作为参考，通过除以由标准峰得来的峰值系数来校准信号峰的m／z或丰度值。最常见和最简单的无目标归一化策略是将质谱中的所有分子离子丰度除以总离子数（TIC）。该方法假定每个谱图的丰度变化处于同一水平。改进的算法引入了统计学理论，比如丰度中值法、滑动窗口归一化（SWN）［9］、概率商归一化（PQN）［10］、方差稳定归一化（VSN）［4］等。有研究证明，与未进行归一化或使用简单的中值法的图像相比，SWN策略具有获取更清晰图像的优势［9］。已有研究系统地评估了针对每个像素对应的质谱图的信号峰丰度的7种归一化方法［10］。图1显示了6种归一化方法中各个单独像素点中的质谱峰值丰度除以的系数，“信息峰”是指通过两种不同的方法进行变量选择后仍然存在的峰值。归一化过程也可分为谱内（Intra）－归一化（计算每个像素中质谱的归一尺度因子）和谱间（Inter）－归一化（在图像样本中的所有质谱使用统一归一尺度因子［11］）。

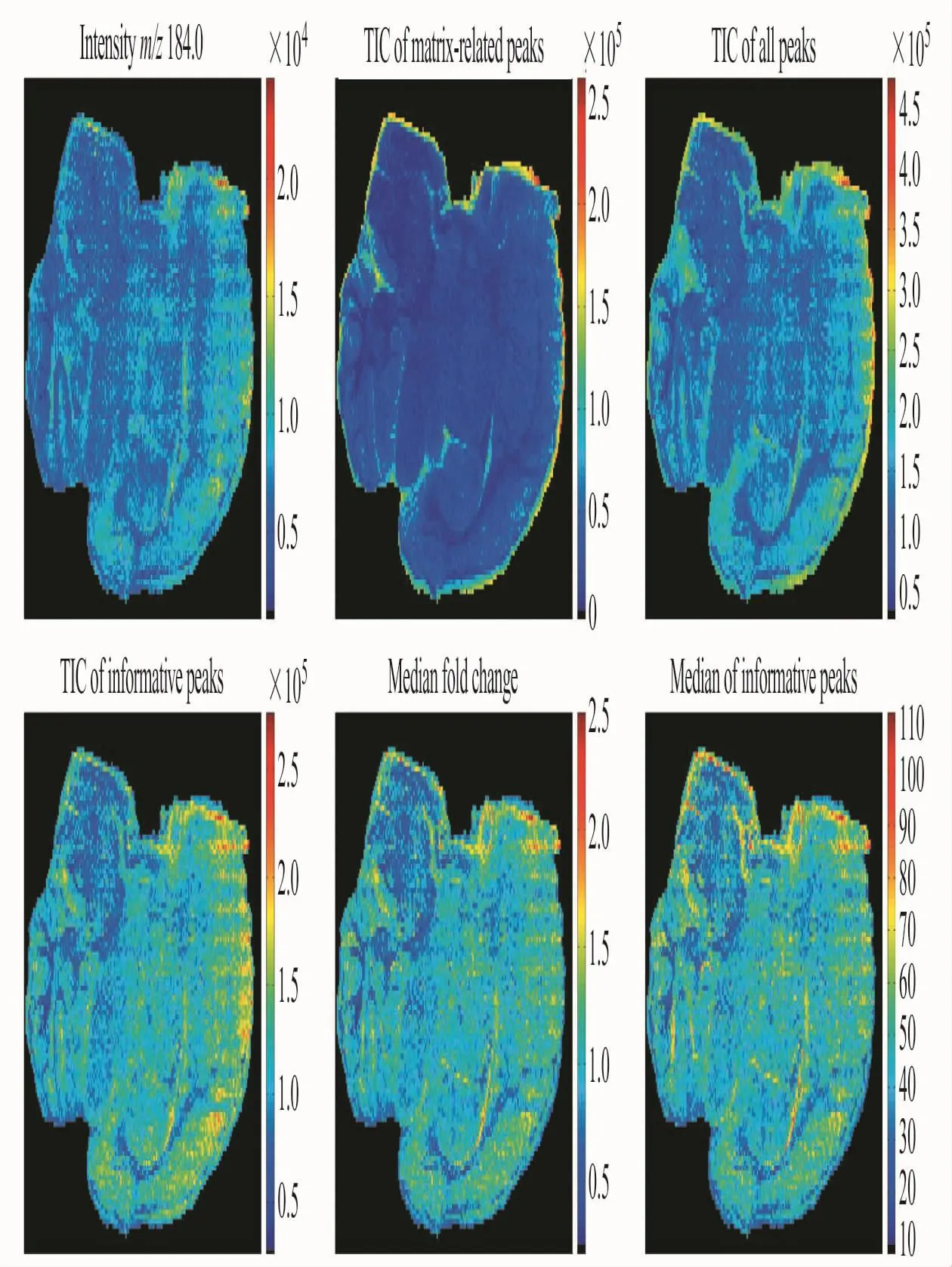
图1 大鼠脑样本矢状面切片MALDI－MSI数据的归一化处理。六张图代表六种归一化方法，每幅图像的色阶代表着归一化因子系数，每个单独像素中的质谱数据将除以这个因子进行处理。红色表示被高因子除，蓝色表示被低因子除Fig．1 Normalization of MALDI MSI data of the sagittal rat brain section．The color scale for each image represents the factor by which the spectrum in an individual pixel would be divided for six normalization methods．Red represents the division by a higher factor and blue a lower factor．Reprinted with permission from Fonville et al．［10］Copyright 2012 American Chemical Society

1．2 峰检测和m／z－图像去噪

峰检测，也称为质心化［12］或峰提取［13］，这是质谱数据分析中的一个常见步骤，它的目的是将一种化合物的质谱信号组合成一个峰，从而将质谱谱图简化为信号峰列表。通常，MSI谱图中的信号峰列表被构建为m／z－图像，这种图像是基于MSI数据集中所有谱图中具有特定m／z的峰的丰度值［13］。在随后的数据处理阶段，全变差（Total Variation）最小化和Chambole算法可用于对m／z－图像进行保持边缘去噪。该去噪过程使用了在常规MALDI－MS去噪中不会考虑的MSI数据中的空间信息。另一种方法，即两步峰值选择法也被引入到了MALDI－MSI空间成像信息的处理中。该方法首先去除与基质相关的噪声峰，然后根据m／z－图像的丰度分布来设定可解释变异（Variance Explained）阈值完成空间质谱数据的去噪［10］。

2 降维处理

2．1 线性降维处理

线性降维与矩阵分解和变换密切相关。在MSI数据的统计分析中，矩阵因式分解是一个将二维MSI数据矩阵分解成其他矩阵乘积的数学过程。本综述将根据不同的分解动机和矩阵约束来讨论几种用于MSI数据集降维的矩阵分解方法。

图2显示了基于4种常见的线性降维方法提取主因子，包括：主成分分析（PCA）、非负矩阵分解（NMF）、最大自相关因子（MAF）和概率潜在语义分析（PLSA）。前期的研究已经证明降维处理可在不同组织切片间（如疾病和健康组织［11，15－17］）提供带有更显著差异的和更好的可视化效果。另外，降维算法对生物标记物的确认也非常有帮助，更为自动图像识别提供了依据［5］。在医药领域，还有其他降维算法包括应用于研究不同种类药片中化合物的具体组成和分布［18］。为了获得更加一致和准确的结论，有的研究会结合多种降维策略。比如，Jones等人将三种矩阵分解方法（PCA、NMF、MAF）和两种聚类算法（K－means聚类和模糊C－means聚类）生成的多个分量图像集成为一致性图用于图像分析［19］。

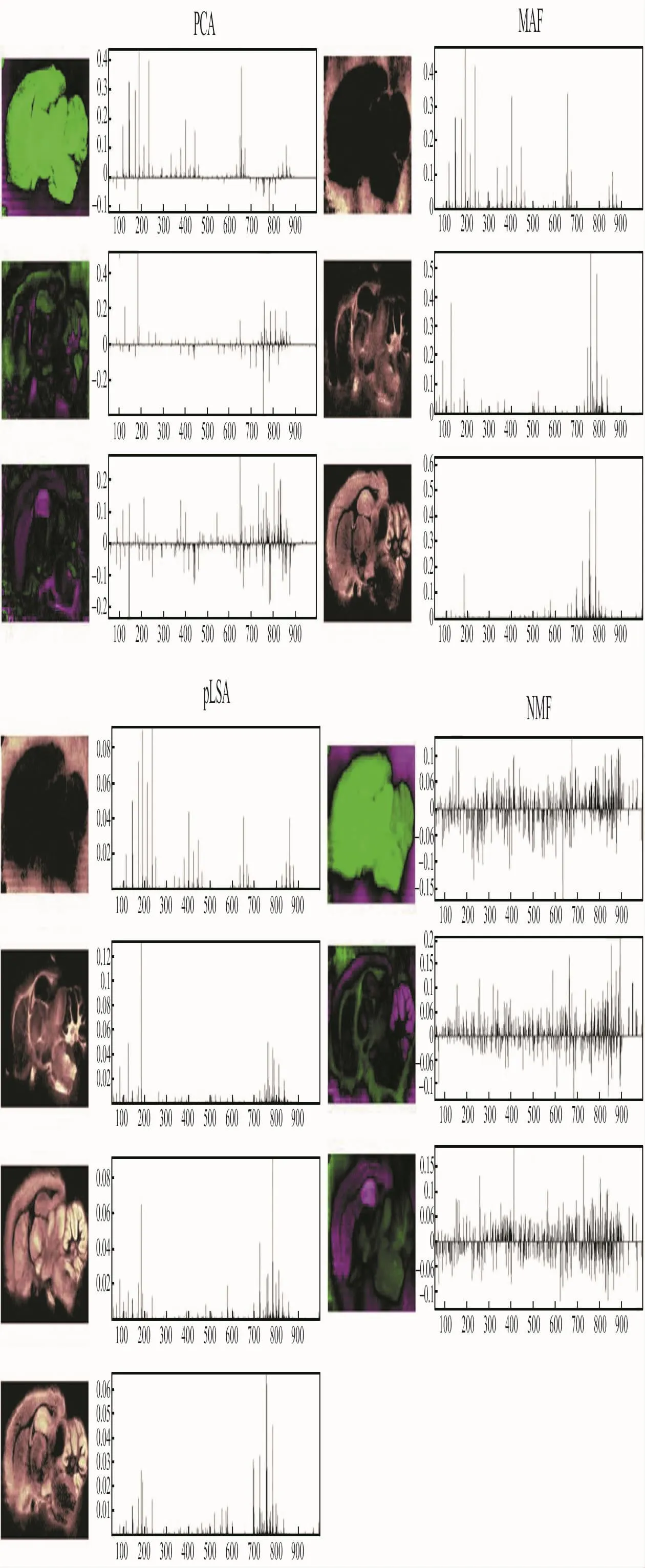
图2 应用主成分分析（PCA）、非负矩阵分解（NMF）、概率潜在语义分析（PLSA）和最大自相关因子（MAF）对大鼠大脑矢状面切片的MALDI－MSI图像进行特征因子选择Fig．2 Selected factors from principal component analysis（PCA），non－negative matrix factorization（NMF），maximum autocorrelation factor（MAF），and probabilistic latent semantic analysis（PLSA）applied to a MALDI－MSI image of a sagittal section of rat brain．Reprinted with permission from Race et al［14］．Copyright 2016American Chemical Society

2．1．1 主成分分析（PCA） PCA可以将坐标系（包括像素位置的维度和MSI谱图中选定信号峰的丰度值）线性变换为正交主成分坐标系。PCA方法通常选择一个或两个主成分因子来表示MSI数据集，这会有效地减小数据维数，去除不相关的噪声，同时保留更多数据信息。第一主成分展示了数据集中的最大方差。许多综述和研究讨论了用于监督和非监督 MSI分析的 PCA 方法［5，7，9，11，14－16，18－21］。主成分分析也可以与其他几种方法相结合使用，包括随机投影主成分分析（RP－PCA）［22］、主成分分析－线性判别分析（PCA－LDA）［23］和主成分分析－符号判别分析（PCA－SDA）［24］。随机投影可以将m／z－图像中的所有像素点映射到较少的像素点上并计算投影分数，从而使数据维数变小。这种方法也可单独用于MSI超谱数据分析［25－26］。PCA 与其他算法的结合可用于数据集的分类和聚类分析［23－24，27］。

2．1．2 独立成分分析（ICA） ICA可以将MSI数据集分解为若干统计学相互独立的正交子成分的线性组合。通常是利用最大化某种非高斯性度量，而不是类似PCA中的方差最大化［18，21，28］。ICA主要针对非高斯分布样本点。

2．1．3 非负矩阵分解（NMF） NMF是用两个非负矩阵的乘积来重构MSI数据矩阵的另一种矩阵因子分解方法。为了使原始矩阵与重建的矩阵乘积之间的误差最小化，通常会使用欧氏距离等最优化函数［14，17－19］。

2．1．4 最大自相关系数（MAF） 在MAF分析中，所使用的线性变换类似于PCA和ICA。唯一的区别是MAF是通过最大化MSI数据集中相邻像素间的自相关指标来实现因子分解［14，19］。

2．2 非线性降维

随机邻域嵌入（SNE）是一种非线性降维方法，它将高维数据展示在二维或三维空间中以便更好地可视化［29］。改进的方法包括t－分布SNE（tSNE）和分层SNE（hSNE）已被用于 MSI数据集的可视化分析［16，30－33］。tSNE根据t分布和 KL散度计算相似概率分布，将数据定位在低维图中［30，32－33］。hSNE 将高维MSI数据分层地显示在低维空间中，每层具有不同程度的可视化信息［31］。

2．3 特征选择

数据降维通常分为特征提取和特征选择［34］。在前面的章节中，我们总结了通过将高维空间中的数据投影到低维空间中来减少维度的常见的特征提取方法。特征选择可以看作是另一种数据降维方法，它通过选择重要的和包含信息较多的特征（即质谱数据中的信号峰的m／z值），以排除噪声信号，提高计算效率。特征选择的其他优势还包括提高无监督图像像素聚类的准确性，以及避免有监督分类分析中的过拟合问题［7，35］。信息特征选择还可通过应用收缩t统计量（Shrunken t－Statistics）来比较类别或片段的质心（由一种分类或一个图像区域中的平均质谱数据定义）与整体的质心的差异来实现［36］。另一项研究提出基于Wilcoxon秩检验和Kolmogorov－Smirnov检验获得显著性差异程度p值，并选择p值最小的信号峰作为分类特征，从而实现特征选择［37］。

3 聚类

聚类是数据挖掘和统计分析中常用的无监督方法。聚类方法可对MSI像素数据点进行分组，同一聚类簇中的像素数据点的谱图、峰值表或生成的主成分特征相比于其他簇中数据点具有更大的相似性。在二维和三维MSI分析中，聚类主要用于自动构建分割图像，以便更好地实现可视化和进行生物评价［38－39］。如图3所示，根据分割图［39］，不同的解剖学结构可以很容易地被识别和分辨。空间分割图还有助于揭示肿瘤区域在组织中的分布［40］、肿瘤的功能异质性［41］以及借助微蛋白质组学进行肿瘤分类［42］。图切割聚类法已应用于比较小鼠脑组织切片的DESI和MALDI－MSI的离子抑制效果，它可以区分奥氮平（Olanzapine）的高、低离子抑制区［43］。MSI数据集中无监督聚类分析的另一个应用是分析在大麦发芽过程中具有组织特异性和时间依赖性的代谢物模式［44］。下面介绍最常用的几种MSI聚类算法。

3．1 K－均值（K－means）算法

K－means算法将MSI数据集划分为k个聚类簇，k的值是预定义的数。其划分主要依据每个像素点的特征向量与k个聚类簇的质心向量之间距离，像素点被分到距离最近的那个聚类簇中。质心向量在第一次迭代时是随机分配的，然后根据所有簇内像素点的平均值更新每个簇的质心向量，重复该过程直到质心向量不再改变。其中计算距离常常是使用欧氏距离［40－42，45－46］。其它的距离度量也有在MSI数据分析研究中使用，如 Cityblock（曼哈顿）距离、相关性距离和余弦距离［39，43，47－49］。K－means算法已集成到各种MSI分析软件工具中［11，50－51］。

3．2 层次聚类（HC）

HC建立了一个聚类簇的层次树，称为树状图（Dendrogram）。集聚（Agglomerative）或分裂（Divisive）策略被递归地执行，每次递归对最相似或最不相似的像素数据点分别进行合并或分割，并生成树的一层分支节点。相似性的计算同样基于距离度量，如欧氏距离。该方法已广泛应用在MSI图像分割分析［8，16，40，52－53］。HC算法还用于通过将具有最小簇间距离的相邻峰集合并到一个簇中来实现 MSI谱图的数据降维，每个簇的范围是根据质谱中的m／z值来计算确定的［54］。

图3 图切割聚类法跟MSI中现有聚类算法的比较，算法应用于大脑冠状面（k＝7）和矢状面（k＝20）切片的MSI图像以及作为比较的Allen大脑图集（图底部）。大鼠脑冠状面数据是以45×45μm的像素获取并且共包含20 000个像素，大鼠脑矢状面数据是以100×100μm的像素获取并且共包含12 500个像素Fig．3 Comparison of existing clustering algorithms used in MSI，and graph cuts clustering applied to MSI images of a coronal（k＝7）and sagittal（k＝20）brain sections as compared to the Allen brain atlas（bottom）．Coronal mouse brain data was acquired with 45×45μm pixels and contained a total of 20 000pixels，sagittal rat brain was acquired with 100×100μm pixels and contained 12 500pixels．Reprinted with permission from Dexter et al［39］．Copyright 2017American Chemical Society

3．3 自组织图（SOM）

SOM是一种神经网络类型，由高维的MSI数据集训练得到，用低维节点图表示。在MSI数据分析中，SOM被用于数据降维、聚类和可视化［32］。而作为一种改进的SOM方法，分层双曲线自组织图（H2SOM）是为MSI图像分割和无监督聚类而开发引入的［44］。

3．4 其他聚类算法

图切割法是另一种聚类算法，已有研究将其与K均值法和层次聚类法进行了比较［39］。比较结果证实它在小鼠冠状面和矢状面脑切片的MSI数据集中能生成更清晰的分割图像（图3）。模糊C－均值（C－means）算法不同于K－均值和HC等硬聚类算法。除了使用了模糊集思想，这种算法还采用了新的距离度量方式。模糊C－均值算法已用于对一种植物（桉树）叶片的MSI代谢组学数据集进行聚类［9］。利用期望最大化的概率聚类算法也被用于对大鼠脑冠状切面产生的MSI数据进行处理［46］。

4 分类

分类算法是一种有监督的学习策略，它根据训练后的分类器对给定的数据集进行分类。这些分类器由训练数据集中选定特征构成的数学函数进行定义。训练过程主要依赖于具有明确类标签的数据集。它不同于一般的聚类算法，因为聚类算法没有将先验知识用于分析［7，35－36］。MSI数据分析中使用的大多数分类方法都集中在区分健康和疾病条件下的样本数据的各种生物学应用，以及在不同阶段协助诊断疾病。通过从数据集中选择包含信息较大的特征，可由经过训练的分类器进行诊断测试［16］。为了提高分类器的分类性能，各种算法包括支持向量机（SVM）、随机森林（RF）和PCA等被用来获取和训练分类器。在本节中，我们将描述这些用于MSI图像分类的算法策略。

4．1 支持向量机算法

支持向量机（SVM）是一种非概率型分类算法，已经在生物信息学领域得到了广泛的应用。根据不同的核函数，SVM可以生成线性分类器或非线性分类器。训练过程包括最优化超平面的计算，以划分不同标记类中的数据点。联合使用SVM和PCA算法可将人脑组织样本中感兴趣区域ROI的MSI图像像素点分为三类，即非病理性的人脑垂体区、分泌性和非分泌性垂体腺瘤区［27］。最近有研究利用支持向量机（SVM）算法建立了基于ALλ和ATTR淀粉样蛋白的肽组成的分类模型，对淀粉样变性疾病进行诊断［55］。另外，SVM在肿瘤类型诊断和甲状腺病变诊断中的应用已有报道［56］。

4．2 随机森林算法

随机森林是一种利用投票将多个决策树构造为分类器的集成型分类方法。在每个树的每个节点中，通过分裂情况来确定特征（MSI数据处理中的m／z值可作为特征）的随机子集中最优的特征，训练样本集是由所有样本中采用Bagging或Bootstrap的取样方法有放回的选出的。随机森林算法已与主动学习（AL）策略和改进的样本标记方法相结合用于对MSI数据集进行多分类［3，57］。

4．3 其他统计和机器学习算法

通过对给定样本和每个肿瘤类型的统计模型间相似性分数计算，可以建立用于肿瘤类型分类和鉴定的统计框架［54］。Veselkov等人使用了递归最大间距准则（RMMC）方法来处理基于脂质分子特征的结肠癌组织类型分类问题。与基于偏最小二乘法（PLS）的算法以及它们以前所使用的PCA－LDA方法相比，它具有更高的分辨精确度［4］。在人类肾细胞癌MSI数据集上，另一个基于空间收缩质心策略的统计模型被用于对正常组织和癌组织进行分类。与PLS－DA算法相比，该算法在提供有用信息的特征显著减少的情况下仍能获得类似的分类性能［36］。

套索算法（LASSO）模型也已在前期的研究中被使用，它通过选取小代谢产物和脂质分子作为诊断特征来区分正常前列腺和前列腺癌［58］。该研究指出，在组织样本MSI所有像素点的质谱图中，小代谢物葡萄糖和柠檬酸盐的平均离子信号可作为癌症诊断的分类器（图4）。已有研究将三种分类器包括LDA分类器、朴素贝叶斯分类器（NBC）和决策树分类器（DTC）进行了系统性的比较［37］。深度学习是近年来解决具有大信息量的数据集中分类问题的有效方法。深度卷积神经网络方法（CNNs）也被应用于处理基于MSI的肿瘤分类，比如诊断两种肺部肿瘤亚型以及辨别肺部肿瘤和胰腺肿瘤［59］。

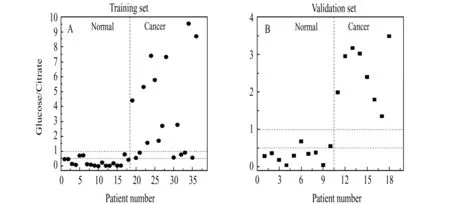
图4 负离子模式的DESI－MS针对葡萄糖／柠檬酸盐的离子信号丰度比图，用于（A）训练集（18个良性和18个癌症样本），以及（B）验证集（10个良性和8个癌症样本），其中信号是从单个组织样本获得的所有像素质谱中的葡萄糖和柠檬酸盐的平均离子信号。从这些图中可以看出，当葡萄糖／柠檬酸盐信号丰度比大于1时，一个组织可归类为癌症；当葡萄糖／柠檬酸盐信号丰度比小于0．5时，该组织可归类为良性Fig．4 Negative ion mode DESI－MS ion signal intensity ratios for glucose／citrate are plotted for（A）the training set（18 benign and 18cancer specimens），and（B）the validation set（10benign and 8cancer specimens）by averaging the ion signals of glucose and citrate from all pixels acquired from the individual tissue sample．From these plots，a tissue can be classified as cancer when glucose／citrate signal ratio is＞1，and benign when the ratio is＜0．5．Reprinted with permission from Banerjee et al［58］．Copyright（2017）National Academy of Sciences

5 MSI软件

前期的综述文章对用于MSI数据分析和可视化的软件工具已进行了总结，包括常用的商业软件、免费软件工具和开源软件［7］。因此，我们主要综述过去三年新开发的工具。

用户友好性较好的商业工具MassImager可提供高通量的MSI数据可视化和统计分析功能［5］。文献中报道的用于MSI数据分析的软件基本都是免费的，如BioMap和Datacube。直接比较表明，尽管Biomap具有更好的用户体验和便捷性，但它和Datacube的性能是基本相似的［60－61］。msIQuant是一个MSI可视化工具，可以相对快速加载较大的MSI数据集。新版本的msIQuant引入了减少数据信息熵和压缩算法并可用于高效的数据归档［62－63］。BASTet是OpenMSI工具的一个扩展框架，主要用于网络共享、管理和分析MSI数据［64－65］。MSIdV可通过衡量和比较MSI数据集中不同m／z值的多个分子来实现组织切片的所有区域的生物指标的可视化［66］。

OpenMSI阵列分析工具包（OMAAT）是一个与OpenMSI集成的开源工具。它可以生成每个感兴趣的离子的图像，并协助分析指定空间区域中的一组数据［67］。两个基于R的开源软件包rMSI［68］和massPix［50］也已用于MSI数据处理。rMSI设计了一个用户友好的图形界面（GUI）来可视化MSI图像数据，界面包括空间图像面板、所选的感兴趣区域（ROI）和质谱视图面板。与rMSI不同，Masspix专门针对脂质组学MSI，它专注于绘制单离子分布图并加入了PCA和聚类算法等统计分析功能。pyBASIS是另一个开源平台，它可通过机器学习和模式识别等方法处理多个组织样本中产生的大规模MSI数据集［11］。MsiReader v1．0是该开源工具系列的最新版本，它添加了一些新功能，例如用于分析极性切换数据的极性过滤器、用于成像显示的图像叠加功能以及用于质量保证的质量测量精度（MMA）热图绘制功能［69］。如图5所示，MsiReader v1．0的界面展示了对小鼠脑组织切片的多个MSI数据集的处理情况。

图5 多个图像数据集加载。图示为12个小鼠脑组织矢状面切片中胆固醇［M＋H－H2O］＋的图像Fig．5 Loading multiple imaging data sets．The images presented are for cholesterol［M＋H－H2O］＋in 12sagittal mouse brain tissue sections．Reprinted with permission from ［Springer Nature］：［Springer］［Journal of The American Society for Mass Spectrometry］［MSiReader v1．0：Evolving Open－Source Mass Spectrometry Imaging Software for Targeted and Untargeted Analyses．Bokhart M T，Nazari M，Garrard K P，Muddiman D C［69］］．［COPYRIGHT］（2018）

6 结论

MSI质谱成像技术已成为组织样本切片中分子组分鉴定的一项重要技术。由于数据量大、不同像素中的质谱数据的差异以及实验噪声等因素影响，MSI数据处理仍然具有挑战性。本文中我们综述了MSI数据分析流程中的生物信息学计算策略，包括预处理、数据降维、聚类、分类和软件工具。数据归一化处理在预处理中非常重要，我们也慨括了校正不同像素中数据之间的误差的重要性。矩阵分解法（如PCA、ICA、NMF和MAF）常用于MSI线性数据降维，以去除次要成分因子，提高数据分析效率。我们也介绍了非线性降维算法SNE和基于统计的特征选择方法。本综述还讨论了K－means、HC和SOM等聚类算法在图像分割和生物学评价中的应用。此外，MSI在疾病诊断和生物标记物发现的应用中，有监督分类算法（如SVM、随机森林）是一种有价值的验证标准。预计MSI计算策略的进一步发展将有助于提高MSI数据的质量，并促进MSI技术在生物和临床发展中的应用。

致谢：感谢基础教育信息技术服务湖北省协同创新中心的资助。