学科史视角下的中学STEAM实验教学设计
林庄燕 姜浩哲
华东师范大学教师教育学院(200062)
1 引言
STEAM是Science(科学)、Technology(技术)、Engineering(工程)、Art(艺术)和Mathematics(数学)五门学科英文首字母的缩写。在素质教育时代,STEAM教育以跳出单学科知识培养跨学科知识、能力、思维和价值观而备受重视。但是,尽管STEAM教育的实践需求很高,一个好的STEAM实践案例却并不是那么容易设计的,因而好的STEAM教学设计事实上并不多见。从学科史角度来看,数学和科学的发展动因不仅来自学科内部,更多时候是学科外部的需要促进了学科发展。因而,数学史、科学史中有丰富的、体现学科联系的案例,为我们STEAM实验教学的设计提供了宝贵的素材。本文选取若干个初中数学知识点,基于STEAM实验教学的理念开展教学设计,以期对STEAM教学有所启示与帮助。
2 教学案例设计
2.1 相似三角形的应用
“图像的相似”是初中数学的重难点之一,其中相似三角形的应用更是这章节的重中之重。相似三角形的应用历史十分悠久,在许多文献中就已经提到相似三角形的应用问题,并运用到了相似三角形的定义及性质。
为了将历史知识、历史背景运用到课堂中,并让学生能够实际动手操作,笔者选取若干史料,将其整理成数学情境,并设置问题,将全班学生进行分组,让各个小组分工合作探究,找出解决方案。
任务1:隧道设计问题
古希腊有一座名为“萨莫斯岛”的岛屿,被称为古希腊第八岛屿。公元前6世纪,在萨莫斯岛上修建了一条供水隧道——欧帕里诺斯隧道。已知隧道长为1 036 m,横截面的宽和高各为1.8 m,现在这条隧道笔直穿过一座山。为了缩短建成时间,设计者欧帕里诺斯让工程队从山的两头一起开始挖掘,最后两队在山体中间会合。
“请同学们思考,在2 500多年以前,在那个缺少技术的年代,设计师是如何保证两支工程队伍不偏不倚正好在山底的某处相遇呢?他是如何利用我们学过的相似三角形的性质解决的呢?”小组合作讨论,给出方案。
教师需提供相应的实验模拟工具:岛屿、假山、测量工具、平面地图等。教师引导学生进行思考,并让他们展开讨论,最后呈现小组的方案。教师最后介绍设计者欧帕里诺斯是如何运用了相似三角形知识(定义、判定定理),保证四点共线,创造出这个水利工程奇迹。
任务2:古塔测高问题
古希腊几何学家泰勒斯年轻时游历埃及时对金字塔十分感兴趣,并测量到了金字塔的高度。在没有现代工具的情况下,泰勒斯究竟是如何测得金字塔高度的呢?小组合作讨论,思考泰勒斯是如何运用三角形相似等性质测得该金字塔的高度的,需要哪些工具。请小组合作讨论给出方案以及解答过程。
该任务中教师只为学生提供一座模拟金字塔,让学生自行思考需要除此之外的哪些工具。
任务3:轮船测距问题
在某个沿海的海岸上有一座灯塔,是为了给遇难轮船提供紧急救援而建造的。但是人们常常为不能预测轮船与海岸之间的距离而苦恼。直到有一天泰勒斯解决了这个问题,成功测出了轮船到海岸之间的距离。小组合作讨论,泰勒斯究竟运用了什么方法解决轮船测距问题的呢?请给出相应的方案及解答过程。
教师需要提供相应的实验模拟工具:轮船、塔、平面地图以及测量工具。
评注:上述的问题虽然是历史上与工程问题、测量问题息息相关的问题,但是实际上都离不开数学知识,比如相似三角形的性质等。传统数学课堂上,教师已经为学生提供好数据和测量方式,学生只需要会计算得出结论即可。但是通过STEAM实验的活动,让学生自己寻找测量的方法,并寻找解决的方案,培养学生的观察、猜想、验证等能力。
2.2 折纸中的数学
19世纪开始,折纸在西方已经成为了数学和科学研究的工具,其中较为突出的是日本筑波大学芳贺和夫所发现的折纸几何三大定理,它已经成为了折纸几何学中的基本定理。芳贺和夫在第二届折纸科学国际大会上提出了折纸数理化的概念,并指出折纸数理化中的折纸与普通折纸的三大不同之处。
据统计,折纸在人教版教科书中共出现了26次,但是在现实教学中很多教师只是将折纸看作是一种体验知识的方式而已。事实上,折纸中蕴含着丰富的数学知识,如果能够将折纸恰当地融入课程当中,那么对于促进学生思考、探究其中的数学原理将有很大的帮助。
下面,以小组合作与教师指导相结合的教学形式呈现部分折纸,让学生在折纸这样的STEAM实验活动中体会数学之美。教师可先提前展示一些好看的折纸图案或者作品,吸引学生的注意,让学生感受折纸的趣味与魅力,激发学生兴趣。
活动一:如何通过折纸将正方形的面积分成三等分?
直接抛出这个问题,对于学生来说是有一定难度,因此教师可以先从一个简单的问题入手。该问题其实改编于芳贺三定理中的芳贺第一定理的某一个小结论,作为学生的思考题:如图1所示,将正方形的AB边与CD边重合对折,得到折痕EF;然后再将C点与E点重合对折,得到折痕GH,我们将BC边与AB边的交点记为N,问:N点是AB的三等分点吗?如果N点是AB的三等分点,那么你能将正方形的面积分成三等分吗?
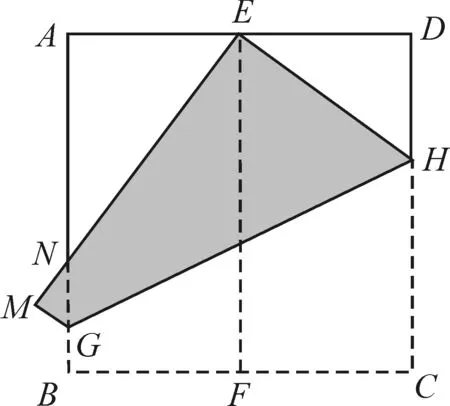
图1 思考题示意图
紧接着分小组讨论,你还能通过什么样的折法将正方形的面积三等分?
学生可能会得到以下做法:
做法一:将正方形ABCD的边AB与CD重合对折,得到折痕EF,过C、E两点折叠,将点D的对应点记做G,将B点与G点重合对折,得到折痕CH,则点H是AB的三等分点,那么很容易可以将正方形三等分。
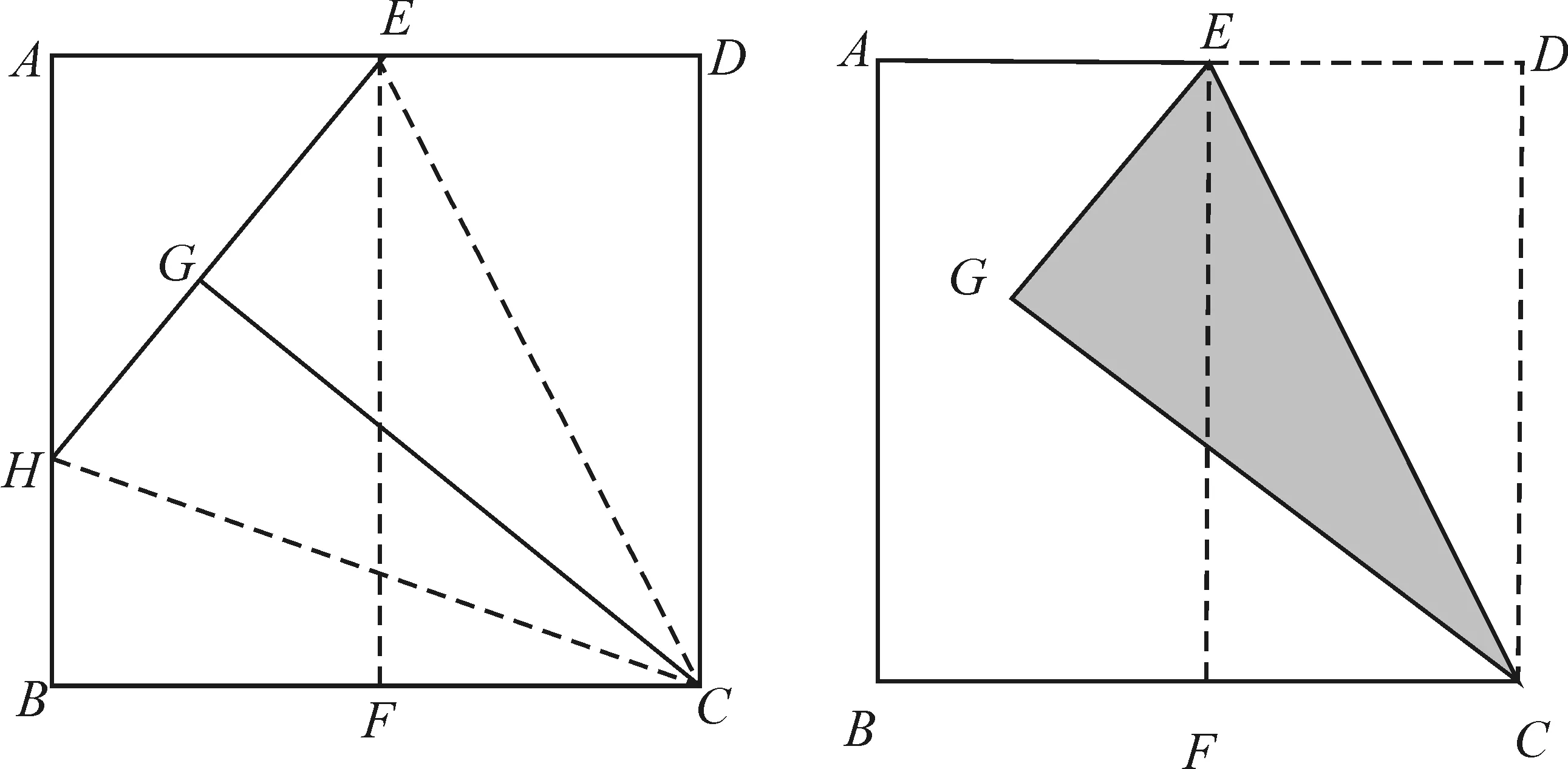
图2 做法一示意图
做法二:将正方形ABCD的边AD与BC重合对折,折痕为EF,然后再分别将AD与EF,BC与EF重合对折,折痕分别为GH和MN;将C点折到GH上,同时让折痕过B点,C点的对应点记为P,BP与EF和MN的交点分别记为Q、R,则线段BC被Q、R三等分。
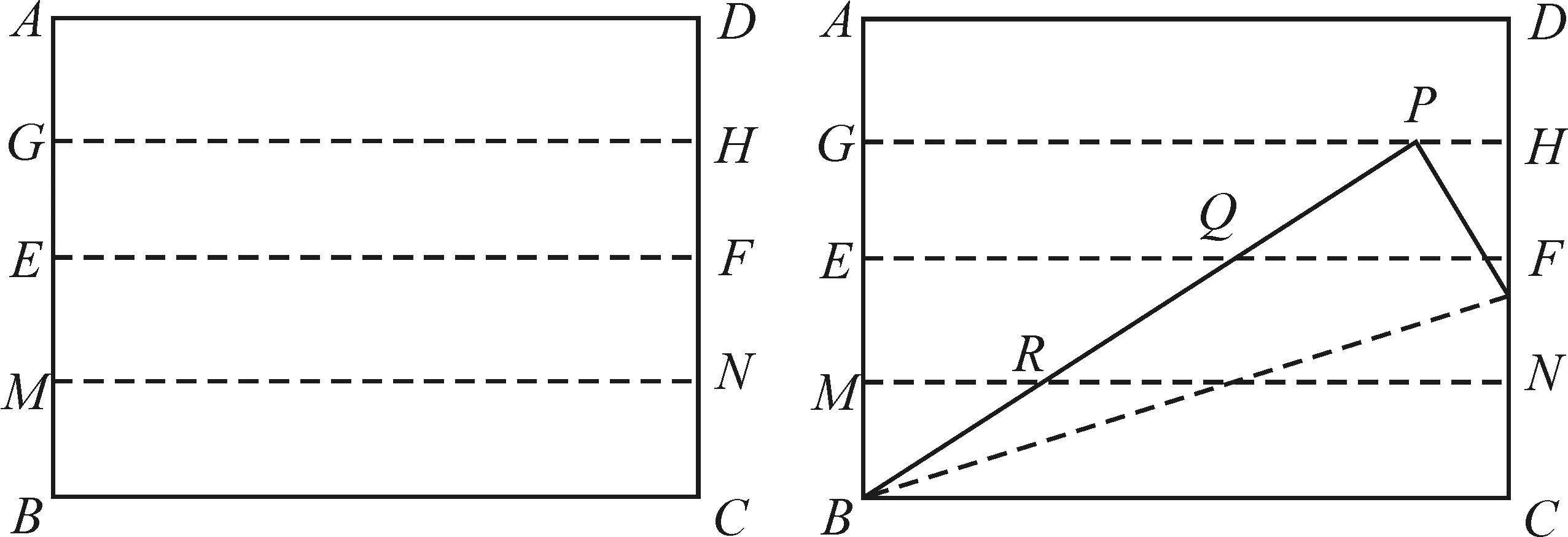
图3 做法二示意图
做法三:将正方形垂直对折,再折叠一条对角线,然后沿着顶边中边和右下角折叠。则过G点平行于BD的直线就是三等分直线。
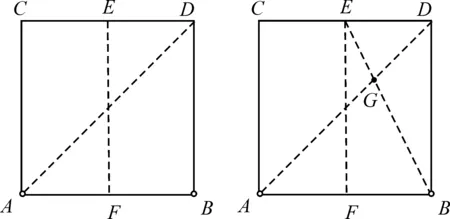
图4 做法三示意图
活动二:如何通过折纸将正方形的面积分成五等分?
这道题的活动的难度系数较大,可由教师给出折的过程,让学生完成剩下的证明工作。
将正方形ABCD的两组对边分别重合对折,得到正方形ABCD四边的中点:E、G、F、H;分别过A、F、B、H、C、E和D、G两点折叠得正方形MNPQ,则该正方形的面积是原来面积的1/5。
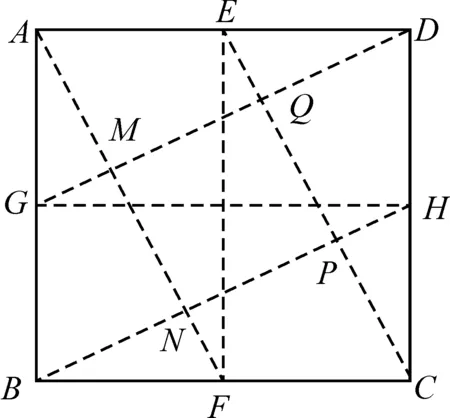
图5 活动二示意图
活动三:如何通过折纸将长方形的面积分成三等分、五等分?
对于长方形面积的奇数等分的做法与上述做法二一样,这里将不作详细阐述。
评注:虽然是简单的折纸过程,但让学生经历了发现问题、分析问题、得出结论、验证结论等过程,并且这其中融合了全等、相似、平行等相关的数学知识。通过折纸这样一个过程让学生自己操作、体验和探索,学生能真正在“做中学”的过程中体会到折纸艺术的美丽与数学思考的火热。
3 分析与讨论
从实验目的来看“相似三角形的应用”属于探索型的STEAM实验,而“折纸中的数学”一开始让学生探究如何让正方形面积三等分,而后验证,因此属于探究型与验证型相结合的STEAM实验。从实验工具来看都是实物实验,且体现多种STEAM实验的特征。在“相似三角形的应用”中,教师为学生提供历史上多个与工程、测量等相关的数学问题背景,让学生通过实物假山、金字塔、测量工具等,真实模拟测量场景,探索测量的方法并找寻解决方案,体现了工具性、操作性、情境性和探究性等实验教学特征。在“折纸中的数学”中,教师通过演示一种折纸的方式,引导学生探索出更多的面积三等分的折纸方式,主要使用的工具以正方形纸片为主,通过演绎推理,体现了工具性、操作性和探究性等实验教学特征。
以上所涉及的两个教学设计均利用STEAM学科史料进行实验探究,并且在合作探究中获得了相关的STEAM知识,具体内容见表1。

表1 实验教学涉及的STEAM知识
4 启示与展望
以上两个案例以数学史、科学史为基石、以实验教学为纽带、以学科联系为导向,在STEAM的新视野、新理念下开展了教学案例设计。展望STEAM实验教学,机遇与挑战并存。
(1)STEAM实验多方位培养学生的素养。不同于传统课程教师教,学生学的方式,STEAM实验更多是将课堂交给学生,让学生在各种技术的帮助下,在动手操作中,去探索数学、理解并应用STEAM知识。通过STEAM实验教学,大大提升了学生学习的兴趣和学习的主动性,加强了学生的合作意识,给予了学生充分发挥其创造力的空间。
(2)STEAM实验对教师提出更高要求。对于开展STEAM实验的课程,教师需要花费更多的时间与精力去设计这样一堂课。教师不仅需要有足够的知识储备,制作相应的教具,使用相应的计算机技术,还需要考虑学生的学情,布置合适的任务,保证STEAM实验的可实施性,让学生可接受、可操作。对于学生的活动能够给予恰当的评价及建议。
(3)数学史、科学史与STEAM教育的结合为数学史、科学史融入课堂提供了新的视角。数学史其中一个教育价值“文化之魅”下包含了学科联系、社会角色、审美娱乐等多个维度,这些维度为数学史与STEAM教育的相结合提供了很好的理论基础。我们期待,未来能开发出更多的关于数学史、科学史与STEAM教育相结合的教学案例。
(4)“STEAM+”馆校结合可以成为常规教育教学的延伸和拓展。近年来,馆校结合教育的兴起在一定程度上也推动了STEAM实验教学的发展,学生的学习不再局限于课堂和教师,科学博物馆等教育已然成为兴趣课堂的理想场所,实验教学也不再局限于学校实验室,科学博物馆实验展览、实验体验等都为STEAM实验教学创造了良好的契机。因此,“STEAM+”馆校结合可以成为常规教育教学的拓展,让博物馆的奇妙旅行充满知识的味道,也让学校的教学充满无限延伸的可能。

