涡街提频振荡水柱驱动压电发电理论分析

杜小振，李周杰，康 辉，张 咪，于 红

(1.山东科技大学 机械电子工程学院，山东 青岛 266590；2.中国石油大学(华东) 理学院,山东 青岛 266580)

0 引言

研究微小型波浪驱动发电实现远海无线监测节点供能具有重要意义[1]。早期研究以波浪能驱动空气透平法拉第电磁发电为主[2]，近年来，利用具有机电耦合效应压电功能材料发电代替电磁发电，结构简单，易小型化[3]，但波浪频率低，转化效率和发电功率低，研究发现，系统输出能量随压电谐响应频率提高而增加[4]。为此，林政[5]设计了机械增频式波浪压电发电装置，将1 Hz入射波增频达到29.5 Hz的激振频率，并作用于压电发电悬臂梁发电结构上。流场中基于卡门涡街效应形成流体激振频率有利于提高振动频率并驱动压电发电微电源能量转换效率和输出电量。Rui Zhang等[6]利用氧化锌(ZnO)、Jie He等[7]利用锆钛酸铅(PZT)压电材料相继提出基于卡门涡街效应风能驱动纳米发电供能的风速测量仪。Marco Demori等[8]设计实现了涡街激振压电发电为流速和温度传感节点供能，可提供100 μW电量。文晟等[9]采用亥姆赫兹谐振腔作为风压谐振放大和涡脱频率调节装置研究基于卡门涡街效应的风力压电浮能器，测试输出电能达13.6 mW。本文在卡门涡街激振研究基础上提出利用波浪进入振荡水柱(OWC)气室压缩气体产生的周期性气流，经卡门涡街绕流圆柱钝体产生高频气压，驱动压电钹发电。

1 OWC气室出口气流理论分析

基于卡门涡街效应提频的OWC驱动压电发电装置示意图如图1所示。图1中，Po为压力采集管出口压强；Pi为压力采集管入口压强；V为换能气室体积；v为气室顶部出口排出气体流速；da为钹型压电振子外径；db为钹型压电振子内腔顶部直径；dc为钹型压电振子内腔直径。推导了气室内的水动力学计算模型并分析了气室出口处的气体流速。计算了气体流经钝体产生高频卡门涡街激振空气压力，并驱动钹型压电发电输出电能。

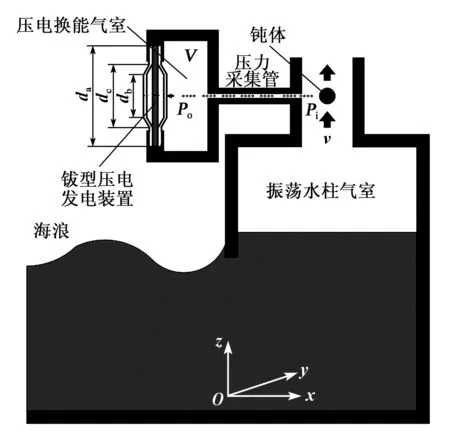
图1 涡街提频振荡水柱驱动压电发电

1.1 气室压强求解

振荡水柱波浪能采集气室为半潜箱体，假定流体均匀，不可压缩，无粘性，无旋，忽略表面张力，则流场内速度势Φ可定义为

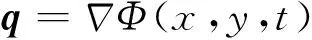
(1)

对式(1)中的速度势求偏导运算，即

(2)

假设Φ在气室内、外域衔接区满足压力与速度连续条件，应用格林函数计算规则线性波流场内的Φ为入射势Φi与散射势Φj的叠加[10]：

Φ=Φi+Φj

(3)

在有限水深单一频率、单一方向入射波作用下，Φi为[11]

(4)

式中：h为水深；k，β分别为入射波波数和方向角。

波高为H时，入射波引起的Φj[12]为

Φj=∬SHoσSG(P;Q)dS

(5)

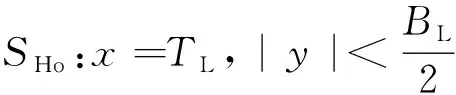
σS由第二类Fredholm方程[13]及满足边界条件用离散化数值方法求解，则有

(6)

在内、外域衔接处，应满足流体速度与压力连续条件，保证内、外域衔接条件为

(7)

式中：n0为内域法向量；n1为外域法向量，n0=n1。

格林函数解有初始条件或边界条件的非齐次微分方程，求解速度势，Wehausen和Laiton[14]以三维脉动源的形式给出了满足边界条件的Green函数：

(8)

G(x,t,x0,τ)=δ(t-τ)G0+Gf(x,t,x0,τ)

(9)

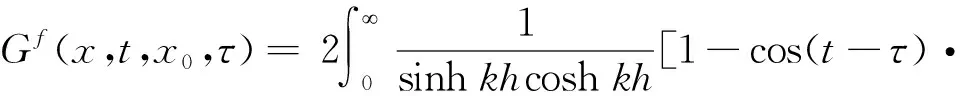
cosh[k(z+h)]J0(kR)dk

(10)

[F(X,Y-Z,T)+F(X,2-

Y-Z,T)]

(11)

(12)

cosh(kV)J0(kX)dk

(13)

当X>1时，使用Fourier级数将F0表示[16]为

(14)

当0≤X≤1时，采用切比雪夫多项式逼近F0为

(15)

式中bmn为分析Green函数在各种参数范围内的插值系数。

n=0,1,2,3,4，…

(16)

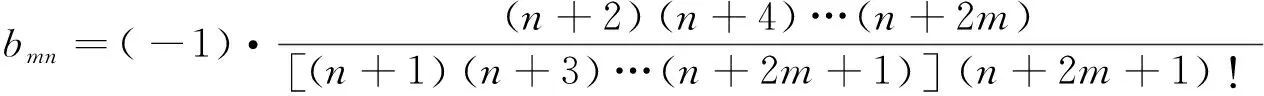
(17)

式中：m=1,2,3,4，…;n=0,1,2,3，…。

F(X,V,T)=F+(F-F)

(18)

(19)

F-F

(20)

式中Re表示复数的实部

假设OWC气室内的气室压强随振荡水柱一起按正弦函数变化，且与气室内液面振荡速度成正比，压强求解式[17]为

(21)

式中τ为气室空气沉降振荡有效阻尼系数。

1.2 OWC气室出口流速求解

波浪进入OWC内形成振荡水柱，其往复运动驱动气室内空气产生振荡压强。忽略空气的可压缩性[18]，通过气室顶端出口处的气体体积流量Q(t)与气体压强P(t)为正比关系：

(22)

式中：ρ为水的密度；β为透平系数；Ra为顶部出口半径。

气室模型结构尺寸为1.2 m×1.0 m×1.5 m，水深1 m，气室前墙吃水深为0.3 m，入射周期T=0.85 s，气室前墙与气室波面达到共振[19]，气室压强峰值达到65 Pa。共振时流量最大，气室出口流量与流速、压强成正比。

2 气室出口卡门涡激高频激励分析

振荡水柱在气室内驱动空气流动压强频率与波浪频率一致，压缩空气流经钝体形成涡街高频气流，其能量转换装置如图1所示。气流经钝体后产生压差为Pa=(Pi-Po), 假设能量转换气室中为可压缩、刚性气体；压力采集管中为不可压缩、刚性气体，则压电换能气室空气压强和钹形压电振子激振频率求解过程如下[20]：

流体的体积弹性模量比Ea为

(23)

气室内空气体积的变化与压强的关系为

(24)

利用流体的连续方程可得

(25)

式中：do为压力采集管直径；v为压力采集管内气体流速。

由式(24)、(25)可得：

(26)

根据Poiseuille’s定律得压力收集管中摩擦阻力f：

f=8πμvL

(27)

式中：L为压力收集管的长度；μ为动力粘度。

根据牛顿第二定律得压力管内气体流速微分方程：

(28)

将式(26)、(27)代入式(28)得

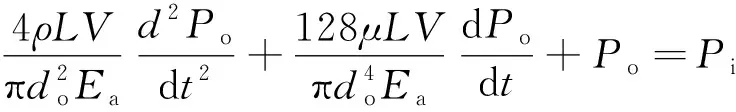
(29)

式(29)的单自由度二阶振动方程标准形式为

(30)

采样涡街产生的空气压力的角频率为

(31)

涡街激振频率[21]为

(32)

式中：Dz为圆柱钝体直径；v0为气室出口流速；v1为声速；St为斯特劳哈尔数。

3 钹型压电发电振子受涡街激振气压作用响应分析

将压电片夹在两片钹型金属片之间组成钹型压电发电振子(见图1)，受循环涡街气压作用，压电片承受的负载F与应力Q为[22]

(33)

(34)

式中：γ为泊松比；E为弹性模量；δ为偏转绕度；tc为铜帽圆片弹性层厚度；Hc为空腔高度；A1、A2为功能常数；S为钹型压电振子受压面积。由压电功能材料电场本构方程得压电振子的开路电压：

|Q×cosθ·tp·d33|

(35)

外接负载电压和功率计算分别为

(36)

(37)

式中：RL为外接负载电阻；C为静态电容；ω1为外接负载角频率；Rs为压电片等效内阻；tp为压电片厚度；d31、d33为压电系数；θ为压电片受力角。

4 发电系统输出特性讨论

海浪进入气室后压缩空气从顶部出口快速流出遇到Dz=50 mm的圆柱形钝体产生卡门涡街激振。空气压力频率随海浪周期变化关系如图2所示。当海浪周期TW<0.85 s时，海浪周期增加，OWC气室波高增加，压缩空气产生的压强随海浪周期增加逐渐增大，涡街激振频率与气室出口流速、压强成正比。TW=0.85 s时，气室前墙入射波与气室内水面发生共振，压强最大，出口空气流速最快，涡街激振频率达600 Hz，提频效果最优。TW>0.85时，随海浪周期增大，在气室内产生大量的非线性波，存在波能损耗。

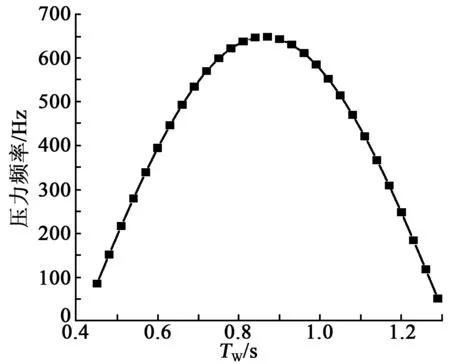
图2 涡街提频空气压力频率与TW关系

高频气压通过压力收集管道(L=170 mm、do=6 mm)进入压电能量转换气室并驱动钹型压电振子发电，钹型振子外径da=29 mm,dc=17 mm,db=5 mm。气压驱动钹型压电振子发电功率与激振频率关系如图3所示。由式(32)～(35)计算可得涡街激振频率为0～700 Hz，压电振子的电能量随压力频率的增大快速提高，激振压力频率提高能量转换效率和输出功率较明显。

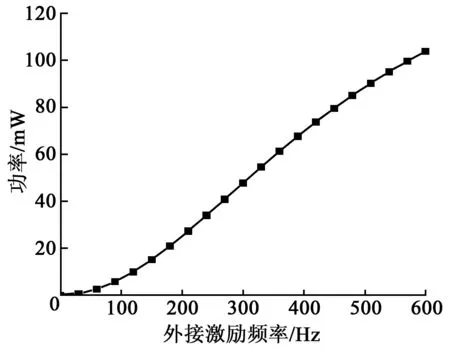
图3 发电功率与激振频率关系

压电发电功率与涌入气室的TW存在密切关系，TW=0.65～1.1 s时，由式(22)～(31)可得TW与钹型压电振子发电输出功率的关系如图4所示，输出电能稳定在65～80 mW。

图4 发电功率与TW的关系

卡门涡街产生的压电换能气室的压力频率与气室出口处钝体直径有关，随钝体直径的增大而降低，由式(28)～(31)计算钹型压电振子产生的能量随钝体结构变化如图5所示。气室出口流速提高，压力频率增大，因此，钹型压电振子产生的电能随之提升，如图6所示。

图5 发电量与钝体直径关系

图6 发电量与气室气体流速的关系

5 结束语

振荡水柱收集波浪能在气室内产生高压、高速空气动能并作用于圆柱形钝体，基于卡门涡街效应获得高频空气压力进入压电换能气室驱动钹型压电振子发电，解决低频海浪驱动压电发电中能量转换率低的问题。分析波浪与空气相互作用的水动力学特性、利用压电能量转换理论、卡门涡街效应理论推导计算得出,气室前墙入射波与气室内的波面产生共振涡街激振高频气压达650 Hz，随着钝体尺寸的增大，提频效果减弱，随着气体流速的提高，系统输出电能提高，当海浪周期在0.6～1.1 s时，系统输出70～80 mW稳定电能。